Математика (курс 14)
Производится n независимых испытаний, в которых вероятность наступления события A равна p. Вероятность того, что событие A наступит m раз
вычисляется по формуле Бернулли
вычисляется по формуле Байеса
равна p(1-p)
вычисляется по формуле Муавра-Лапласа
Вероятность выиграть в кости равна 1/6. Игрок делает 120 ставок. Каким асимптотическим приближением можно воспользоваться, чтобы сосчитать вероятность того, что число выигрышей не будет меньше 15?
интегральной формулой Муавра-Лапласа
распределением Пуассона
надо сосчитать по формуле Бернули
локальной формулой Муавра-Лапласа
В ящике в 5 раз больше красных шаров, чем черных. Найти вероятность p того, что вынутый наугад шар окажется красным
1/6
5/6
0.5
0.6
Завод в среднем дает 27% продукции высшего сорта и 70% – первого сорта. Найдите вероятность того, что наудачу взятое изделие не будет высшего или первого сорта.
0.03
0.97
0.7
0.27
Завод в среднем дает 28% продукции высшего сорта и 70% – первого сорта. Найдите вероятность того, что наудачу взятое изделие будет или высшего, или первого сорта.
0.02
0.98
0.97
0.7
Куплено 500 лотерейных билетов. На 40 из них упал выигрыш по 1 руб., на 10 – по 5 руб., на 5 – по 10 руб. Найдите средний выигрыш, приходящийся на один билет.
0.35
0.28
1
2
MX = 5, MY = 2. Используя свойства математического ожидания, найдите M(2X - 3Y).
2
3
4
5
На отрезке длиной 20 см помещен меньший отрезок L длиной 10 см. Найти вероятность того, что точка, наудачу поставленная на большой отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
0.1
1/4
0.5
0.2
На некотором заводе было замечено, что при определенных условиях в среднем 1.6% изготовленных изделий оказываются неудовлетворяющими стандарту и идут в брак. Равной чему можно принять вероятность того, что наугад взятое изделие этого завода окажется качественным? Сколько примерно непригодных изделий (назовем это число M) будет в партии из 1000 изделий?
р = 1.6
p = 0.984
p = 0.16
p = 0.016
Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Чему равна вероятность того, что из 200 взятых наугад изделий 2 окажутся неисправными?
0.271
0.01
0.024
0.001
Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры.
0.4
0.75
0.5
0.25
Имеется группа из n несовместных событий Hi, в сумме составляющих все пространство, и известны вероятности P(Hi), а событие A может наступить после реализации одного из Hi, и заданы вероятности P(A/Hi). Известно, событие A произошло. Вероятность, что при этом была реализована Hi вычисляется по формуле
Байеса
Муавра-Лапласа
Полной вероятности
Бернулли
Два стрелка стреляют по разу в общую цель. Вероятность попадания в цель у одного стрелка 0.6, у другого – 0.7. Найти вероятность того, что цель будет поражена двумя пулями.
0.56
0.42
0.96
0.88
Вратарь парирует в среднем 30 % всех одиннадцатиметровых штрафных ударов. Какова вероятность того, что он возьмет ровно два из четырех мячей?
0.2811
0.3248
0.2646
0.3145
Бросаются 2 монеты. Вероятность того, что выпадут и герб, и решка, равна
0.5
1/4
1/3
0.3
MX = 1.5. Используя свойства математического ожидания, найдите M(2X+5).
5
3
8
6.5
Человеку, достигшему 20-летнего возраста, вероятность умереть на 21-м году жизни равна 0.01. Какова вероятность того, что из 200 застраховавшихся человек в возрасте 20-ти лет один умрет через год?
0.246
0.256
0.297
0.271
Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора – 0.05, второго – 0.08. Найти вероятность того, что при включении прибора оба элемента будут работать.
0.874
0.928
0.826
0.871
Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора – 0.03, второго – 0.06. Найти вероятность того, что при включении прибора откажет только второй элемент.
0.0582
0.06
0.0671
0.0938
Количество поражений шахматиста в течение года имеет распределение Пуассона с параметром λ=6. Вероятность того, что шахматист в течение года проиграет не более двух партий равна
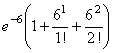
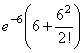
Возможные значения случайной величины X таковы: x1 = 2, x2 = 5, x3 = 8. Известны вероятности: р(X = 2) = 0.4; р(X = 5) = 0.15. Найдите р(X = 8).
0.45
0.4
0.55
0.5
Число грузовых машин, проезжающих мимо бензоколонки, относится к числу легковых машин, как 3:2. Известно, что в среднем одна из 30 грузовых и одна из 25 легковых машин останавливается для заправки. Найти вероятность того, что проезжающая машина будет заправляться.
0.5
0.04
0.036
0.33
Человеку, достигшему 20-летнего возраста, вероятность умереть в течение 20 лет равна 0.02. Какова вероятность того, что из 200 застраховавшихся на 20 лет человек в возрасте 20 лет ни один не умрет?
0.0183
0.0235
0.0145
0.256
Выпущено 100 лотерейных билетов, причем установлены призы, из которых 8 по 1 руб., 2 – по 5 руб. и 1 – 10 руб. Найдите вероятности p0 (билет не выиграл), p1 (билет выиграл 1 руб.), p5 (билет выиграл 5 руб.) и p10 (билет выиграл 10 руб.) событий.
p0=0.89; p1=0.08; p5=0.02; p10=0.01
p0=0.89 p1=0.08; p5=0.01; p10=0.02
p0=0.88; p1=0.08; p5=0.02; p10=0.01
p0=0.9; p1=0.08; p5=0.02; p10=0.01
Если вероятность р некоторого события неизвестна, а для оценки этой вероятности производится n испытаний, то 95%-ый доверительный интервал для величины р находится по формуле
Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Чему равна вероятность того, что из двух взятых наугад изделий окажутся неисправными оба?
0.001
0.02
0.01
0.0001
События A и B называются несовместными, если:
р(AB)=0
р(AB)=1
р(AB)=р(A)р(B)
р(AB)=р(A)+р(B)
Если вероятность события A есть р(A), то чему равна вероятность события, ему противоположного?
1-р(A)
0.5
1
0
Вероятность суммы любых случайных событий A и B вычисляется по формуле:
р(A+B)=р(A)+р(B)-2р(AB)
р(A+B)=р(A)+р(B)
р(A+B)=р(AB)
р(A+B)=р(A)+р(B)-р(AB)
Человеку, достигшему 60-летнего возраста, вероятность умереть на 61-м году жизни равна 0.09. Какова вероятность того, что из трех человек в возрасте 60 лет хотя бы один умрет через год? (с точностью до 4-х знаков после запятой).
0.8281
0.2464
0.9100
0.7536
Задана таблица распределения случайной величины. Найти р(X < 3). 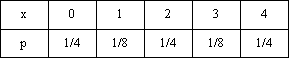

1/2
5/8
3/8
3/4
Вероятность выиграть в рулетку равна 1/38. Игрок делает 190 ставок. С помощью какой таблицы можно найти вероятность того, что он выиграет не менее 5 раз?
надо сосчитать по формуле Бернулли, асимптотические формулы дадут большую ошибку
распределения Пуассона
функции Лапласа Ф(х)
плотности нормального распределения
Количество Х принимаемых по телефону за час звонков имеет распределение Пуассона. Среднее количество принимаемых за час звонков λ=5. Вероятность того, что за час будет принято точно 3 звонка равна
Вероятность появления события А в испытании равна 0.1. Чему равно среднеквадратическое отклонение числа появлений события А в одном испытании?
0.3
0.9
0.09
0.03
Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка 0.1, для второго – 0.2 и для третьего – 0.15. Найти вероятность того, что в течение некоторого часа хотя бы один из станков потребует внимания рабочего.
0.635
0.612
0.365
0.388
Бросаются 2 кубика. Вероятность, что сумма выпавших очков равна 3, составит
1/6
1/3
1/18
3/36
В среднем каждое сотое изделие, производимое предприятием, дефектное. Если взять два изделия, какова вероятность, что оба окажутся исправными?
0.9801
0.213
0.01
0.001
Для проверки на всхожесть было посеяно 2000 семян, из которых 1700 проросло. Равной чему можно принять вероятность p прорастания отдельного семени в этой партии? Сколько семян в среднем (назовем это число M) взойдет из каждой тысячи посеянных?
p=0.15; M=150
p=0.85; M=850
q=3/20; M=800
p=17/20; M=750
Бросается 5 монет. Какова вероятность того, что три раза выпадет герб?
5/16
11/16
17/32
15/32
Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0.7, у другого – 0.8. Найти вероятность того, что цель будет поражена.
0.94
0.8
0.85
0.96
Станок-автомат производит изделия трех сортов. Первого сорта – 80%, второго – 15%. Чему равна вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта?
0.15
0.95
0.2
0.8
При изготовлении детали заготовка должна пройти четыре операции. Полагая появление брака на отдельных операциях событиями независимыми, найти (с точностью до 4-х знаков после запятой) вероятность изготовления нестандартной детали, если вероятность брака на первой стадии операции равна 0.02, на второй – 0.01, на третьей – 0.02, на четвертой – 0.03.
0.0800
0.0777
0.9222
0.9200
В группе 25 студентов, из которых отлично учится 5 человек, хорошо – 12, удовлетворительно – 6 и слабо – 2. Преподаватель вызывает студента. Какова вероятность того, что вызванный студент или отличник или хорошист?
8/25
0.85
17/25
0.5
В круг радиусом 10 помещен меньший круг радиусом 5. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.
0.5
0.75
0.25
0.05
Вероятность любого события всегда удовлетворяет следующему условию
может принимать значения, меньшие 0
может принять любое значение
она не меньше 0 и не больше 1
всегда строго больше 0
Для контроля качества продукции завода из каждой партии готовых изделий выбирают для проверки 1000 деталей. Проверку не выдерживают в среднем 80 изделий. Равной чему можно принять вероятность того, что наугад взятое изделие этого завода окажется качественным? Сколько примерно бракованных изделий (назовем это число M) будет в партии из 10000 единиц?
p = 0.08
p = 0.8
p = 0.92
p = 0.7
Рулетка размечается с помощью меток – 00, 0, 1, ...36. Метки при игре не имеют преимуществ друг перед другом. Игрок делает 114 попыток. Какова вероятность ни разу не выиграть?
0.05
0.07
0.03
0.08
Монету бросали 100 раз. 70 раз выпал орел, для проверки гипотезы о симметричности монеты строим доверительный интервал и проверяем, попали ли мы в него. По какой формуле строится доверительный интервал, и что даст проверка в нашем конкретном случае?