Исследование операций (курс 2)
Методом статистических испытаний (Монте-Карло) можно находить не только вероятности событий, но и средние значения (математические ожидания) случайных величин. При нахождении средних значений (математических ожиданий) случайных величин мы будем пользоваться уже не теоремой Бернулли, а законом _______________
Верны ли утверждения? Оптимальное решение, принятое на конкретном шаге, должно обеспечить максимальный выигрыш: А) не на данном конкретном шаге, а на всей совокупности шагов, входящих в операцию; В) на данном конкретном шаге
А – нет, В – нет
А – да, В – нет
А – нет, В – да
А – да, В – да
Поведение марковского процесса на долгосрочном горизонте планирования характеризует его _________ от начального состояния системы
независимость
случайную зависимость
линейную зависимость
частичную зависимость
Ситуации, в которых сталкиваются две (или более) враждующие стороны, преследующие различные цели, причем результат любого мероприятия каждой из сторон зависит от того, какой образ действий выберет противник, называются _________ ситуациями
Верно ли высказывание? А) Среднее время безотказной работы элемента равно полной площади S, ограниченной кривой надежности и осями координат В) В качестве характеристики надежности элемента часто применяется среднее время непрерывной работы
А – да, В – нет
А – да, В – да
А – нет, В – нет
А – нет, В – да
Под постепенным отказом разумеется отказ устройства, связанный
с некачественной работой вспомогательных элементов
с выходом из строя основных элементов
с выходом из строя главных элементов
с постепенным ухудшением («сползанием») его характеристик
Динамическое программирование — это _________ планирование многошагового процесса
Верны ли утверждения? А) Недостаточность информации всегда опасна, и за нее приходится платить В) Однако в условиях сложной ситуации всегда полезно представить варианты решения и их возможные последствия в такой форме, чтобы сделать произвол выбора менее грубым, а риск — минимальным
А – нет, В – да
А – да, В – нет
А – нет, В – нет
А – да, В – да
Математическая теория конфликтных ситуаций - это теория
вероятностей
надежностей
игр
случайных величин
Динамическое программирование в некоторых источниках называют
программированием для решения задач планирования материальных ресурсов производства
программированием для решения бухгалтерских задач
программированием для выработки прогноза на будущее
многоэтапным программированием
В ситуациях неопределенными могут быть:
правила игры
условия выполнения операции
цели (задачи) операции, успех которой далеко не всегда может быть исчерпывающим образом охарактеризован одним-единственным числом — показателем эффективности.
сознательные действия противников или других лиц, от которых зависит успех операции
Оптимальные решения, полученные с учетом и без учета дисконтирования
никогда не совпадают
могут различаться
несопоставимы
всегда совпадают
Внезапный отказ возникает в какой-то, вообще говоря, _________ момент времени. Примерами внезапных отказов могут служить: перегорание электро- или радиолампы, обрыв проводника, пробой конденсатора и т.п.
Верны ли утверждения? А) Во многих задачах исследования операций нам приходится сталкиваться с проблемой принятия решения в условиях неопределенности В) В задаче неопределенность в той или другой степени может относиться также и к целям (задачам) операции, успех которой далеко не всегда может быть исчерпывающим образом охарактеризован одним-единственным числом — показателем эффективности
А – да, В – да
А – нет, В – нет
А – да, В – нет
А – нет, В – да
При решении ряда практических задач исследования операций (в области экономики, военного дела и т.д.) приходится анализировать ситуации, в которых
результат любого мероприятия каждой из сторон не зависит от того какой образ действий выберет противник
результат любого мероприятия каждой из сторон зависит от того, какой образ действий выберет противник
сталкиваются две (или более) враждующие стороны, преследующие различные цели
сталкиваются только две стороны, преследующие различные цели
Закон больших чисел (теорема Чебышева) гласит
при большом числе независимых опытов математическое ожидание случайной величины не изменяется
при большом числе независимых опытов среднее арифметическое наблюдаемых значений случайной величины почти наверняка мало отличается от ее математического ожидания
в любом случае среднее арифметическое наблюденных значений случайной величины почти наверняка мало отличается от ее математического ожидания.
при большом числе независимых опытов среднее арифметическое наблюдаемых значений случайной величины сильно отличается от ее математического ожидания
Верны ли утверждения? А) Теория статистических решений является теорией проведения статистических наблюдений, обработки этих наблюдений и их использования. Б) Статистические модели представляют собой игру двух лиц (человека и природы) с использованием человеком дополнительной статистической информации о состояниях природы
А - нет, Б - да
А – да, Б - да
А - да, Б - нет
А - нет, Б - нет
В идее пошаговой оптимизации есть принципиальная тонкость:
каждый шаг оптимизируется сам по себе
каждый шаг оптимизируется сам по себе, без "оглядки на будущее", на последствия принимаемого "шагового" решения
каждый шаг оптимизируется с учетом принятого предыдущего решения
каждый шаг оптимизируется не сам по себе, а с "оглядкой на будущее", на последствия принимаемого "шагового" решения
Уравнение общих затрат для ситуации, когда учитываются затраты на покупку товара, - это
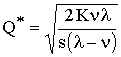
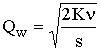
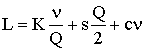
Установите соответствие между понятиями
метод Монте-Карло
математический метод, разработанный для эффективного решения некоторого класса задач математического программирования. Этот класс характеризуется возможностью естественного (а иногда и искусственного) разбиения всей операции на ряд взаимосвязанных этапов
«принцип квазирегулярности».
каково бы ни было состояние системы S в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах
принцип оптимальности" Беллмана
интенсивности потоков событий, переводящих элемент из одного состояния в другое состояние, зависят не от самих численностей состояний, а от их средних значений (математических ожиданий) 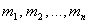
метод динамического программирования
метод математического моделирования случайных явлений, в котором сама случайность непосредственно включается в процесс моделирования и представляет собой его существенный элемент
Модели динамического программирования применяются
для выработки управленческих решений при резком увеличении размеров производства, разделении труда, увеличении численности работающих
для выработки управленческих решений при увеличении численности работающих и необходимости планирования материальных ресурсов
при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа
при планировании материальных ресурсов, резком увеличении размеров производства, разделении труда
В обозначении fi(j) оптимального ожидаемого дохода в задаче с конечном горизонтом планирования i- это_______,а j – это________
номер состояния системы, номер этапа
номер этапа, номер решения
номер этапа, номер состояния системы
номер решения, номер состояния системы
Теория ________________ решений является теорией проведения статистических наблюдений, обработки этих наблюдений и их использования
Вероятность того, что данный элемент в данных условиях будет работать безотказно в течение времени 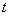 , называется
, называется
надежностью элемента (в узком смысле слова)
работоспособностью элемента
безотказностью элемента
отказоустойчивостью элемента
Путь от исходного до завершающего события - это
наикратчайший путь
критический путь
подкритический путь
полный путь
Верны ли утверждения? А) Так же как в жизни конкретное осуществление процесса складывается каждый раз по-иному, так же и в результате «розыгрыша» мы получаем один экземпляр — одну «реализацию» случайного явления В) Для сложных операций, в которых участвует большое число элементов (машин, систем, людей, коллективов) и в. которых случайные факторы сложным образом взаимодействуют между собой, метод статистических испытаний, как правило, оказывается проще аналитического
А – да, В – нет
А – нет, В – нет
А – да, В – да
А – нет, В – да
Верны ли утверждения? А) Методом статистических испытаний (Монте-Карло) можно находить не только вероятности событий, но и средние значения (математические ожидания) случайных величин В) При использовании метода Монте-Карло пользуются теоремой Бернулли, а не законом больших чисел (теоремой Чебышева)
А – нет, В – да
А – нет, В – нет
А – да, В – нет
А – да, В – да
В качестве характеристики надежности элемента часто применяется среднее время безотказной работы, т.е. математическое ожидание величины Т
Метод Монте-Карло иначе называется методом
динамики средних
статистических испытаний
скользящего среднего
наименьщих квадратов
Путь, имеющий наибольшую продолжительность среди других возможных путей сетевого графика, - это
подкритический путь
наикратчайший путь
критический путь
полный путь
В теории статистических решений основные правила могут быть ___________________и рандомизированными
генеративными
выигрывшными
детерминированными
определенными
Динамическое программирование часто помогает решить задачи, где
необходимо найти оптимальный вариант плана производства
необходимо составить оптимальный прогноз плана производства
переборный алгоритм требует высокую точность вычислений
переборный алгоритм потребовал бы очень много времени
Каждая непосредственно взятая из практики конфликтная ситуация очень сложна, и ее анализ затруднен наличием многих привходящих, несущественных факторов. Чтобы сделать возможным математический анализ ситуации, надо
отвлечься от этих второстепенных факторов
построить упрощенную, схематизированную модель ситуации
построить схематизированную модель ситуации
построить упрощенную модель ситуации
План выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, - это
сетевая модель
график привязки
сетевой график
путь
Верны ли утверждения? А) Метод Монте-Карло в исследовании операций есть метод математического моделирования случайных явлений, в котором сама случайность непосредственно включается в процесс моделирования и представляет собой его существенный элемент В) Каждый раз, когда в ход операции вмешивается тот или другой случайный фактор, его влияние имитируется с помощью специально организованного «розыгрыша» или «жребия»
А – нет, В – да
А – да, В – да
А – нет, В – нет
А – да, В – нет
Задача теории игр — выработка рекомендаций по рациональному образу действий участников _____________
Укажите соответствие между понятиями и их обозначениями
ненадежность элемента
надежность элемента
математическое ожидание величины Т
дисперсия случайной величины
«При большом числе независимых опытов среднее арифметическое наблюдаемых значений случайной величины почти наверняка мало отличается от ее математического ожидания» - это теорема ___________
Решение многоэтапной задачи путем полного перебора всех вариантов приемлем, когда количество вариантов
невелико
неизвестно
достаточно велико
конечно
Модели динамического программирования не применяются:
при разработке принципов выравнивания занятости в условиях колеблющегося спроса на продукцию
при расчете численности работающих, при планировании материальных ресурсов, необходимых для выполнения плана производства
при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены
при распределении дефицитных капиталовложений между возможными новыми направлениями их использования
Рекуррентное уравнение динамического программирования с конечным числом этапов связывает
оптимальные ожидаемые доходы
векторы состояний
вероятные переходы
оптимальные решения
Вероятность 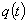 того, что элемент откажет (выйдет из строя) в течение времени
того, что элемент откажет (выйдет из строя) в течение времени 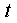 , называется
, называется
неработоспособностью элемента
надежностью элемента
отказоустойчивостью элемента
ненадежностью элемента
Задача первостепенной важности - обеспечение ________ работы всех элементов оборудования технических устройств
Верны ли утверждения? А) В статистической игре природа является разумным игроком, который стремится выбрать для себя оптимальные стратегии. Б) Для всех состояний природы не существует одной наилучшей функции решения
А - да, Б - нет
А - нет, Б - нет
А - нет, Б - да
А – да, Б - да
Верны ли утверждения? А) В сущности, методом «розыгрыша» может быть решена любая вероятностная задача; однако оправданным он становится только в случае, когда процедура «розыгрыша» проще, а не сложнее применения аналитических, вычислительных методов В) Методом статистических испытаний (Монте-Карло) можно находить средние значения (математические ожидания) случайных величин
А – да, В – да
А – нет, В – нет
А – да, В – нет
А – нет, В – да