Многомерные распределения и предельные теоремы
F(x,y) – функция распределения двумерной случайной величины (Х,У); FX(x) – функция распределения случайной величины Х; FУ(x) – функция распределения случайной величины У; Х и У зависимы Какие из утверждений верны?
F(x,y) ≠ FX(x)×FY(y)
F(+¥,+¥) = 1
F(x,y) = FX(x) + FY(y)
F(x,y) = FX(x)×FY(y)
Термины "некоррелированные" и "независимые" случайные величины эквивалентны для случая __ распределения
показательного
нормального
биномиального
Пуассона
X и Y - две случайные величины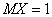 
, 
, 
,
, 
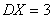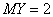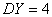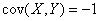D(Х - У) - ? Ответ дайте числом.
, , ,, D(Х - У) - ? Ответ дайте числом.Электростанция обслуживает сеть, в которой 2000 ламп, вероятность включения каждой из них в зимний вечер равна 0,8. Вероятность того, что число одновременно включенных ламп будет более 1800, можно определить при помощи
теоремы Пуассона
теоремы Муавра-Лапласа
теоремы Хинчина
неравенства Чебышева
Берём 100 деталий. Вероятность детали быть бракованной равна 0,02. Х – число бракованных деталей.
P{ Х = 0}
×e-2P{ Х = 1}
2×e-2
P{ Х = 3}
e-2
F(x,y) - функция распределения двумерной случайной величины (X,Y)
F(¥,¥)
0
F(x,y)
Î [0;1]
F(-¥,y)
1
X и Y - две нормально распределённые случайные величины. MX = 1, MY = 2. X и Y некоррелированы. P{X < 1; Y < 2} = ? Ответ дайте числом (десятичной дробью).
Всхожесть семян некоторого растения равна 0,8. Тогда вероятность того, что из 1000 посаженных семян число проросших будет заключено между 750 и 850, можно определить при помощи
теоремы Чебышева
неравенства Чебышева
теоремы Муавра-Лапласа
теоремы Маркова
Величина коэффициента корреляции r(X,Y) заключена в пределах Ответ дайте в виде [a;b]
Случайные величины X и Y связаны линейной зависимостью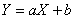 
; r(X,Y) – коэффициент корреляции случайных величин X и Y Какие из утверждений верны?
; r(X,Y) – коэффициент корреляции случайных величин X и Y Какие из утверждений верны?r(X,X – 5) = -1
r(X, X – 5) = 1
r(X, X + 5) = 1
r(X,Y) = 0;
Случайная величина X имеет математическое ожидание mX и дисперсию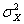 
. Тогда вероятность того, что величина X отклонится от своего математического ожидания не менее чем на 5sX, P{çX - mX ç ³ 5sX } имеет оценку сверху
. Тогда вероятность того, что величина X отклонится от своего математического ожидания не менее чем на 5sX, P{çX - mX ç ³ 5sX } имеет оценку сверху0,04
0,25
0,5
0,2
Берём 100 деталий. Вероятность детали быть бракованной равна 0,03. Х – число бракованных деталей.
P{ Х = 0}
3×e-3
P{ Х = 2}
4,5×e-3
P{ Х = 1}
e-3
Cлучайные величины X и Y независимы. Какие из утверждений всегда верны
M(X + Y) = MX + MY
D(X + Y) = DX + DY
D(X + Y) = DX + DY + 1
M(X + Y) = 1
(aij) - ковариационная матрица 3х3 случайного вектора (X1,X2,X3) X1,X2,X3 - независимы
a11
DX3
a12
0
а33
DX1
Х - случайная величина, МХ = 2, DX = 2. По неравенству Чебышева
P{çX – 2ú ³ 2} £
1/8
P{çX – 2ú ³ 3} £
2/9
P{çX – 2ú ³ 4} £
0,5
(aij) - ковариационная матрица 3х3 случайного вектора (X1,X2,X3)
а33
cov(X1,X2)
a31
cov(X1,X3)
a12
DX3
F(x,y) – функция распределения двумерной случайной величины (Х,У); FX(x) – функция распределения случайной величины Х; FУ(x) – функция распределения случайной величины У; Х и У независимы Какие из утверждений верны?
F(x,y) = FX(x)×FY(y)
F(x,y) = FX(x) + FY(y)
F(5,-¥) = 0
F(x,y) ≠ FX(x)×FY(y)
X - случайная величина, У = -7Х + 3 Чему равен коэффициент корреляции r(X,Y)? Ответ дайте числом.
X и Y - две нормально распределённые случайные величины. X и Y некоррелированы. P{X < 1} = 0,5; P{Y < 2} = 0,4; P{X < 1; Y < 2} = ? Ответ дайте числом (десятичной дробью).
Вероятность того, что в столбике из 150 наугад отобранных монет число монет, расположенных "гербом" вверх, будет от 50 до 75, может быть определена при помощи теоремы
Муавра-Лапласа
Пуассона
Маркова
Чебышева
Пусть f(x,y) – плотность вероятности случайного вектора (X,Y), fX(x) и fY(y) – плотности вероятностей координат этого вектора, причем f(x,y) = fX(x)× fY(y), тогда случайные величины X и Y
независимы
зависимы
слабо зависимы
связаны линейно
Х – случайная величина, МХ = 3, DX = 1, a = 3 Какие из неравенств верны
P{çX – 3ú < 3} ³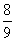 
P{çX – 3ú ³ a} ³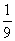 
P{çX – 3ú ³ 3} £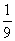
P{çX – 3ú < 3} £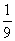
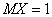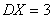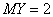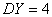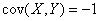X и Y - две случайные величины , , ,, D(2Х - 3У) - ? Ответ дайте числом.
, , ,, D(2Х - 3У) - ? Ответ дайте числом.Случайные величины X и У независимы f(x,y) – плотность вероятности непрерывного случайного вектора (X,Y), fX(x) и fY(y) – плотности вероятностей координат этого вектора
M(X + Y)
fX(x)× fY(y)
D(X - Y)
DX + DY
f(x,y)
MX + MY
f(x,y) – плотность вероятности случайного вектора (X,Y); fX(x) и fY(y) – плотности вероятностей координат этого вектора, причем f(x,y) = fX(x)× fY(y), тогда случайные величины X и Y;
независимы
зависимы
связаны линейно
некоррелированы
Если две независимые случайные величины распределены по закону Пуассона с параметрами l1 и l2, то их сумма имеет распределение
Пуассона с параметром l1 × l2
экспоненциальное с параметром l1 + l2
экспоненциальное с параметром l1 × l2
Пуассона с параметром l1 + l2
F(x,y) - функция распределения двумерной случайной величины (X,Y) f(x,y) - плотность распределения двумерной случайной величины (X,Y)
F(х,y)
1
f(x,y)
F(¥,¥)
Случайные величины X и Y связаны линейной зависимостью 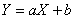; r(X,Y) – коэффициент корреляции случайных величин X и Y; Какие из утверждений верны?
; r(X,Y) – коэффициент корреляции случайных величин X и Y; Какие из утверждений верны?r(X, -X + 5) = -1
r(X,Y) = 0
r(X,-X + 5) = 1
r(X, -X – 5) = -1
F(x,y) – функция распределения двумерной случайной величины (Х,У); FX(x) – функция распределения случайной величины Х; FУ(x) – функция распределения случайной величины У; Х и У зависимы Какие из утверждений верны?
F(x,y) = FX(x) + FY(y)
F(x,y) ≠ FX(x)×FY(y)
F(-¥,5) = 0
F(x,y) = FX(x)×FY(y)
Дискретные случайные величины X и Y независимы, F(x,y) - функция распределения двумерной случайной величины (X,Y) FX(x) – одномерная функция распределения случайной величины X FY(y) – одномерная функция распределения случайной величины У pij - вероятности, определяющие закон распределения двумерной дискретной случайной величины (Х,У).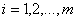 
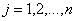
F(x,y)
P{X = xi}×P{Y = yj}
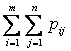
1
pij
FX(x)×FY(y)
Математическое ожидание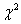 
-распределения с n степенями свободы равно
-распределения с n степенями свободы равно1
n
0
2n
Величина коэффициента корреляции r заключена в пределах
[-1;+1]
[-¥,+¥]
[0,1]
[0,+¥]
Ковариационная матрица случайного вектора (X1,X2,…,Xn) – это матрица n x n, состоящая из элементов aij, равных
aij = M[(Xi – MXi)×(Xj – MXj)]
aij = cov(Xi,Xj)
aij = M(Xi×Xj)
aij = DXi×DXj
X и У независимые случайные величины. Чему равна ковариация cov(X,Y)? Ответ дайте числом.
cov(X,Y) - ковариация случайных величин X и Y r(X,Y) – коэффициент корреляции случайных величин X и Y
r(X,Y)
M[(X – mx)(Y – my)]
D(X + Y)
DX + DY + 2cov(X,Y)
cov(X,Y)
Î [-1;1]
Имеем однородную цепь Маркова с двумя состояниями H1 и Н2. Матрица переходных вероятностей (pij) =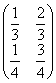 
. Р1 и Р2 - стационарные вероятности Какие из утверждений верны
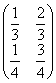. Р1 и Р2 - стационарные вероятности Какие из утверждений верныР2 =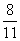 
Р2 =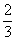 
Р1 =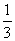 
Р1 =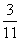 
(aij) - ковариационная матрица 3х3 случайного вектора (X1,X2,X3)
a12
DX1
а33
DX3
a11
cov(X1,X2)
r(X,Y) – коэффициент корреляции случайных величин X и Y; Какие из утверждений верны?
r(X,Y) =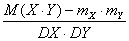 
r(X,Y) =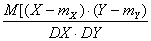 
r(X,Y) =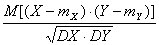 
r(X,Y) =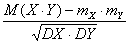 
Случайные величины X и Y связаны линейной зависимостью 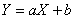; r(X,Y) – коэффициент корреляции случайных величин X и Y; Какие из утверждений верны?
; r(X,Y) – коэффициент корреляции случайных величин X и Y; Какие из утверждений верны?r(X, X - 5) = -1
r(X, X – 5) = 1
r(X, -X + 5) = 1
r(X, -X + 5) = -1
Сумма вероятностей pij, определяющих закон распределения двумерной дискретной случайной величины, равна
1
0,5
2
0
Cлучайные величины X и Y независимы; Какие из утверждений всегда верны
D(2X - 3Y) = 2DX - 3DY
D(2X + 3Y) = 4DX + 9DY
D(2X - 3Y) = 4DX + 9DY
D(2X + 3Y) = 2DX + 3DY
Две независимые случайные величины Х и У распределены по закону Пуассона с параметрами l1 и l2, то их сумма Х + У имеет распределение
Экспоненциальное Пуассона с параметром l1 + l2
Пуассона с М(Х + У) = l1 + l2
Пуассона с параметром l1 × l2
Пуассона с D(Х + У) = l1 + l2
MX = 2, DX = 3; MY = 1, DY = 2; cov(X,Y) = 0
М(2X – Y)
5
D(2X + Y)
14
М(2X + Y)
3
X – случайная величина, имеющая 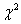-распределения с 3 степенями свободы. МХ - ? Ответ дайте числом
-распределения с 3 степенями свободы. МХ - ? Ответ дайте числомСлучайные величины X и У независимы cov(X,Y) - ковариация случайных величин X и Y r(X,Y) – коэффициент корреляции случайных величин X и Y
D(X + Y)
0
r(X,Х + 5)
1
cov(X,Y)
DX + DY
Характеристическая функция g(t) случайной величины X – это функция
M(eitX)
M(e-tX)
M(e-itX)
M(etX)
Z = X - Y Какие из утверждений всегда верны
D(X + Y) = DX - DY
D(X + Y) = DX + DY - 2cov(X,Y)
M(X + Y) = MX + MY
D(X - Y) = DX + DY
Значение функции распределения F(x, - ¥) есть
0
1
- ¥
0,5
По теореме Муавра-Лапласа вероятность неравенства P{a <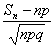 
< b} при больших 
вычисляется следующим образом
< b} при больших 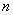вычисляется следующим образом
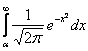
Формула M(CX) = CMX
всегда верна
неверна, если С < 0
неверна
верна, если C > 0