Математика (курс 10)
Дана система линейных уравнений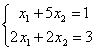 
. Для получения ее решения сходящимся методом Зейделя ее надо записать в виде
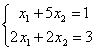. Для получения ее решения сходящимся методом Зейделя ее надо записать в виде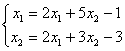
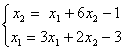
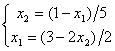
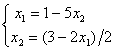
Задана табличная функция y = f(x)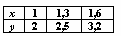 
Линейная интерполяция дает значение y(1,4) равное:
Линейная интерполяция дает значение y(1,4) равное:2,8
2,6667
2,733
2,5667
Дано нелинейное уравнение cos2x - 2x + π ∕ 4 = 0 и начальное условие x0 = π ∕ 4. Первое приближение метода Ньютона x1 будет равно
3π ∕ 4
π ∕ 2
3π ∕ 16
5π ∕ 16
Для линейной системы уравнений вычисления по итерационной формуле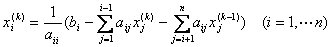 
называют методом
называют методомГаусса
Ньютона
Простой итерации
Зейделя
Условия Фурье при решении одного нелинейного уравнения заключаются в выполнении условий
F′(x) и F″(x) не меняют знак на данном отрезке, F(x0)F ″(x0) > 0
F′(x) > 0, F″(x) ≠ 0, F′(x0) > 0
F(x), F′(x) непрерывны, F ″(x0) > 0
F ″(x), F ″′(x) знакопостоянны, F(x0) ≠ 0
Сходимость итерационного метода решения систем линейных уравнений зависит от
величины правых частей системы
начального приближения системы
вида матрицы системы
количества нулей в матрице
При разложении функции в ряд по многочленам Чебышева на отрезке [-1, 1] погрешность
резко возрастает на концах отрезка и в окрестности x = 0
сильно растет при x = 0
резко возрастает на концах отрезка
распределена на отрезке достаточно равномерно
Результат вычисления интеграла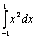 
методом Симпсона с разбиением на два интервала (h = 1) равен
методом Симпсона с разбиением на два интервала (h = 1) равен0,5
2∕3
3∕4
1
Для таблично заданной функции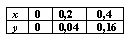 
вычисление y(0,1) с помощью линейной интерполяции дает результат
вычисление y(0,1) с помощью линейной интерполяции дает результат0,02
0,03
0,01
0,22
Для таблично заданной функции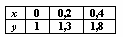 
величина 
, вычисленная с помощью центральной разности равна
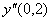величина , вычисленная с помощью центральной разности равна6
5
4,5
4
Задана система линейных уравнений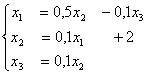 
Один шаг метода Зейделя с начальным приближением { 0 ; 0 ; 0 } дает следующее первое приближение
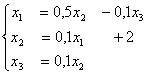Один шаг метода Зейделя с начальным приближением { 0 ; 0 ; 0 } дает следующее первое приближение{ 0,5 ; 2; 0,1 }
{ 0,5 ; 2 ; 0,0205 }
{ 0,3 ; 2,05 ; 2 }
{ 0 ; 2 ; 0,2 }
При вычислении интеграла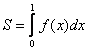 
подынтегральная функция задана таблицей 
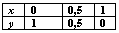Метод трапеций с h = 0,5 дает следующее значение интеграла:
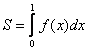подынтегральная функция задана таблицей Метод трапеций с h = 0,5 дает следующее значение интеграла:0,5
1
2/3
1,5
Дана система уравнений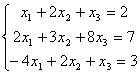 
. Для сходимости итерационного метода ее надо записать в виде
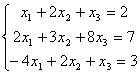. Для сходимости итерационного метода ее надо записать в виде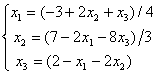
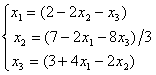
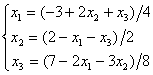
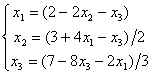
Задана табличная функция y =f(x)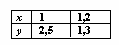 
Интеграл
при вычислении методом трапеций равен
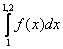Интеграл при вычислении методом трапеций равен1,1
1,3
0,38
1
В таблично заданной функции производная в точке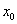 
вычислена с использованием шагов h и 2h . Получены величины 
= 2,4 и 
= 2,7. Погрешность формулы для вычисления производных имеет порядок 
. Тогда уточненное значение производной 
по методу Рунге равно
вычислена с использованием шагов h и 2h . Получены величины 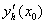= 2,4 и 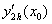= 2,7. Погрешность формулы для вычисления производных имеет порядок 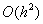. Тогда уточненное значение производной 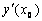по методу Рунге равно2,457
2,3
2,207
2,5
имеет погрешность порядкаДля таблично заданной функции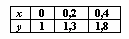 
значение 
,полученное по формуле, использующей центральные разности равно
значение 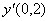,полученное по формуле, использующей центральные разности равно2,5
2
1,8
2,2
Запись нелинейного уравнения в виде x = φ( x ) требуется при решении его численным методом
Гаусса
Ньютона
простой итерации
половинного деления