Вычислительная математика (курс 1)
Установите соответствия. Для дифференциальных уравнений решают следующие задачи
нахождение частного решения уравнения Лапласа, удовлетворяющего дополнительному условию на границе области
краевая задача
нахождение частного решения обыкновенного дифференциального уравнения, удовлетворяющего дополнительным условиям в одной точке области определения решения
задача Коши
нахождение частного решения обыкновенного дифференциального уравнения, удовлетворяющего дополнительным условиям на концах интервала, на котором ищется решения
задача Дирихле
Условие устойчивости явной разностной схемы для одномерного нестационарного уравнения теплопроводности имеет вид
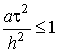
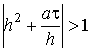
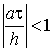
При постановке задачи аппроксимации в качестве аппроксимирующей функции чаще всего используют
ряды Фурье
ряды Гаусса
многочлены
Верны ли утверждения? А) Неявная схема для решения одномерного нестационарного уравнения теплопроводности для расчета использует простую формулу В) Явная схема для решения одномерного нестационарного уравнения теплопроводности всегда устойчива Подберите правильный ответ
А - нет, В - да
А - да, В - нет
А - да, В да
А - нет, В - нет
Укажите соответствие между названиями этапов решения задачи и их содержанием
разработка численного метода решения
математическое описание процесса уравнениями и граничными условиями
постановка задачи
формулировка физической модели процесса
создание математической модели
построение приближенного метода и алгоритма его реализации для решения задачи
При решении систем нелинейных уравнений можно использовать следующий метод
итераций
Ньютона
Гаусса
Расположите табличные функции в порядке возрастания определяемой ими величины 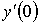 при помощи односторонней правой разности
при помощи односторонней правой разности
x 0 0,2 0,4 y 1 1,4 2,1
x 0 0,2 0,4 y 1 1,9 2,8
x 0 0,2 0,4 y 1 1,5 2,5
Сходимость метода Зейделя обеспечена для следующих систем линейных уравнений
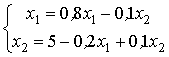
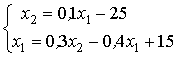
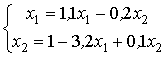
Для величин 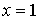 и
и 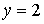 известны абсолютные погрешности
известны абсолютные погрешности 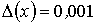 и
и 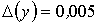 . Абсолютная погрешность произведения
. Абсолютная погрешность произведения 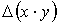 с точностью до 0,001 равна
с точностью до 0,001 равна
Верны ли следующие утверждения? А) Относительная погрешность произведения двух чисел равна сумме относительных погрешностей этих чисел В) Относительная погрешность частного двух чисел равна сумме относительных погрешностей этих чисел Подберите правильный ответ
А – да, В – да
А – да, В – нет
А – нет, В – да
А – нет, В – нет
Для таблично заданной функции вычислите значение 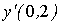 по формуле для центральных разностей (укажите только целую часть) x 0 0,2 0,4 y 1 1,3 1,8
по формуле для центральных разностей (укажите только целую часть) x 0 0,2 0,4 y 1 1,3 1,8
Дифференциальное уравнение 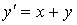 решаем методом Эйлера при
решаем методом Эйлера при 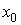 =1 и
=1 и 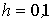 . Сопоставьте каждому начальному приближению
. Сопоставьте каждому начальному приближению 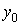 получаемый результат следующего приближения
получаемый результат следующего приближения 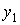
Для обыкновенных дифференциальных уравнений возможны следующие задачи
Коши
Лапласа
краевая
Найти значение 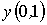 при помощи линейной интерполяции для таблично заданной x 0 0,3 0,6 y 2 2,6 3,8 функции (указать одну цифру после запятой)
при помощи линейной интерполяции для таблично заданной x 0 0,3 0,6 y 2 2,6 3,8 функции (указать одну цифру после запятой)
Найти значение 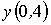 при помощи линейной интерполяции для таблично заданной функции x 0 0,3 0,6 y 2 2,6 3,8 (указать одну цифру после запятой)
при помощи линейной интерполяции для таблично заданной функции x 0 0,3 0,6 y 2 2,6 3,8 (указать одну цифру после запятой)
Отделить корни при решении нелинейного уравнения 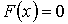 - это значит
- это значит
отделить положительные корни от отрицательных
для каждого корня указать интервал, в котором он будет единственным
расставить корни в порядке их возрастания
для каждого корня указать область притяжения
Задано нелинейное уравнение вида 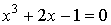 и отрезок
и отрезок 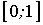 , на котором находится корень. Один шаг метода половинного деления дает отрезок
, на котором находится корень. Один шаг метода половинного деления дает отрезок
Рассматривается задача Коши для системы дифференциальных уравнений 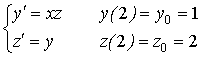 . Сделать один шаг методом Эйлера с
. Сделать один шаг методом Эйлера с 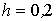
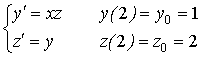 . Сделать один шаг методом Эйлера с
. Сделать один шаг методом Эйлера с Абсолютные погрешности величин x и y равны 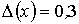 и
и 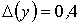 . Абсолютная погрешность разности
. Абсолютная погрешность разности 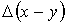 будет равна
будет равна
0,12
0,7
0,1
0,3
Заданы абсолютные погрешности величин x и y, равные 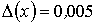 и
и 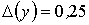 . Верны ли высказывания? А) Абсолютная погрешность разности
. Верны ли высказывания? А) Абсолютная погрешность разности 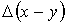 будет равна 0,255 В) Абсолютная погрешность суммы
будет равна 0,255 В) Абсолютная погрешность суммы 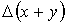 будет равна 0,255 Подберите правильный ответ
будет равна 0,255 Подберите правильный ответ
А – нет, В – нет
А – да, В – да
А – нет, В – да
А – да, В – нет
Симметричная матрица имеет собственные значения
комплексно-сопряженные числа
часть комплексных, часть действительных
все действительные
не имеет собственных значений
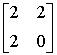
Найти произведение собственных значений матрицы 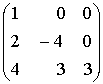 (указать целое число)
(указать целое число)
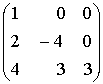 (указать целое число)
(указать целое число)Разностные методы, вычисляющие значение функции в очередной точке при решении задачи Коши для обыкновенного дифференциального уравнения
двухшаговый метод
неявный метод
многошаговый метод
одношаговый метод
Верны ли следующие утверждения? А) Метод Ньютона для решения нелинейного уравнения сходится всегда В) При наличии корня на отрезке метод половинного деления для решения нелинейного уравнения для непрерывной функции сходится всегда Подберите правильный ответ
А- нет, В- нет
А - нет, В - да
А - да, В- да
А - да, В - нет
Расположите системы линейных уравнений в порядке возрастания величины решения 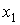 , используя обратный ход метода Гаусса
, используя обратный ход метода Гаусса
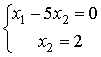
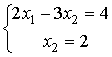
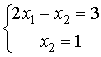
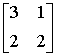
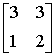
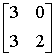
Какие из матриц удовлетворяют условиям диагонального преобладания
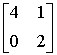
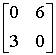
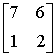
Установить соответствие между определителем матрицы и результатом его вычисления
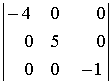
1
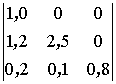
2
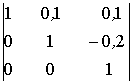
20
Расположите по порядку этапы решения системы линейных уравнений методом итераций
вычисление очередной итерации
проверка условия окончания итерационного процесса
запись системы в виде, удобном для итераций
выбор начального приближения
Система линейных уравнений задана в виде: 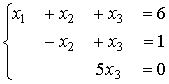 . Сумма решений системы
. Сумма решений системы 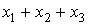 равна (целое число)
равна (целое число)
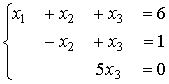 . Сумма решений системы
. Сумма решений системы Функция u(x,y) задана таблицей. Найти значение частной производной 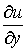 , вычисленное
, вычисленное 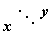 1 1,2 1,4 0,5 1,1 1,4 1,7 0,6 1,3 1,5 2,1 0,7 1,8 1,7 2,0 при помощи левой разности, в точке x = 0,6; y = 1,4 (укажите один знак после запятой)
1 1,2 1,4 0,5 1,1 1,4 1,7 0,6 1,3 1,5 2,1 0,7 1,8 1,7 2,0 при помощи левой разности, в точке x = 0,6; y = 1,4 (укажите один знак после запятой)
Верны ли следующие утверждения при решении систем линейных уравнений? А) Метод простой итерации сходится при выполнении условий Фурье В) Метод верхней релаксации ускоряет сходимость метода Зейделя Подберите правильный ответ
А - нет, В - нет
А - нет, В - да
А - да, В - нет
А - да, В - да
Найти значение 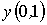 при помощи линейной интерполяции для таблично заданной функции x 0 0,3 0,6 y 2 2,6 3,8 (указать один знак после запятой)
при помощи линейной интерполяции для таблично заданной функции x 0 0,3 0,6 y 2 2,6 3,8 (указать один знак после запятой)
Для решения одного нелинейного уравнения существуют следующие итерационные методы
хорд
Ньютона
сектора
простой итерации
Верны ли следующие утверждения при решении систем линейных уравнений? А) Метод простой итерации требует конечного количества операций В) Метод Зейделя сходится при выполнении условий диагонального преобладания Подберите правильный ответ
А - нет, В - да
А - да, В - да
А - да, В - нет
А - нет, В - нет
Порядок погрешности численного интегрирования
метода Симпсона на элементарном отрезке 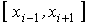
4
метода трапеций на всем отрезке
2
метода Симпсона на всем отрезке
5
Верны ли следующие утверждения при решении систем линейных уравнений? А) Метод Гаусса является прямым методом В) Метод Зейделя является прямым методом Подберите правильный ответ
А - да, В - да
А - да, В - нет
А - нет, В - нет
А - нет, В - да
Укажите соответствие между формулами интерполяции и их названиями
квадратичная по методу Ньютона
квадратичная по методу Лагранжа
линейная
Функция u(x,y) задана таблицей. Найдите значение частной производной 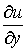 , вычисленное
, вычисленное 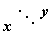 3 3,2 3,4 0,5 1,0 1,4 2,2 0,7 1,2 1,8 2,6 0,9 1,8 2,4 3,4 при помощи левой разности, в точке x = 0,9; y = 3,4 (укажите один знак после запятой)
3 3,2 3,4 0,5 1,0 1,4 2,2 0,7 1,2 1,8 2,6 0,9 1,8 2,4 3,4 при помощи левой разности, в точке x = 0,9; y = 3,4 (укажите один знак после запятой)
Для линейной системы уравнений 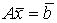 известно
известно 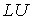 – разложение матрицы
– разложение матрицы 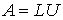 . Тогда количество систем уравнений с треугольными матрицами, к которым сводится решение исходной системы уравнений, будет равно (ответ дайте одной цифрой)
. Тогда количество систем уравнений с треугольными матрицами, к которым сводится решение исходной системы уравнений, будет равно (ответ дайте одной цифрой)
К эллиптическим уравнениям в частных производных относятся уравнения
волновое
Лапласа
Пуассона
К итерационным методам решения систем линейных уравнений относятся методы
Зейделя
простой итерации
Гаусса
Функция u(x,y) задана таблицей. Найдите значение частной производной 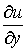 , вычисленное
, вычисленное 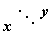 3,0 3,2 3,4 0,5 1,0 1,4 2,2 0,7 1,2 1,8 2,6 0,9 1,8 2,4 3,4 при помощи центральной разности, в точке x = 0,7; y = 3,2 (укажите один знак после запятой)
3,0 3,2 3,4 0,5 1,0 1,4 2,2 0,7 1,2 1,8 2,6 0,9 1,8 2,4 3,4 при помощи центральной разности, в точке x = 0,7; y = 3,2 (укажите один знак после запятой)
Найти значение 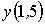 при помощи линейной интерполяции для таблично заданной функции (указать две цифры после запятой) x 0 1 2 y 1 1,9 3,8
при помощи линейной интерполяции для таблично заданной функции (указать две цифры после запятой) x 0 1 2 y 1 1,9 3,8
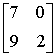
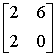
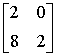
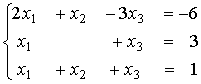
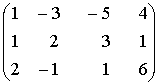
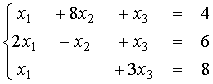

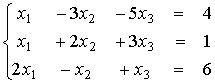

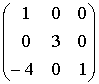 (указать целое число)
(указать целое число)