Основы теории алгоритмов

Множество простых чисел является

Функция, определяемая как число шагов в вычислении машиной Тьюринга, называется

Функция вычисляется по формуле

Если множество не является множеством значений никакой функции, то оно

Если и рекурсия проводится по , то функция равна

Установление соответствия между элементарными высказываниями формальной теории и содержательными высказываниями некоторой предметной области называется

Любая неразрешимая алгоритмическая проблема дает пример множества

Если , то функция в рекуррентной формуле равна

Функция является

Функция, равная единице тогда и только тогда, когда предикат истинен, называется

Множество номеров самоприменимых машин Тьюринга

Существует команд машины Тьюринга

Осмысленные конечные последовательности символов из алфавита L называются

Утверждение формально записывается как

Множество доказуемых утверждений формальной системы арифметики

Геделевский номер, равный , имеет функция

Множество, если оно является множеством значений некоторой вычислимой функции, называется

Если и рекурсия проводится по переменной , то функция равна

Пусть R - рекурсивность, а P - рекурсивная перечислимость. Тогда

Множество натуральных чисел является

Если A рекурсивно, а B - рекурсивно перечислимо, то _____ рекурсивно

w-непротиворечивая формальная система является

Выражением называется

Множество составных чисел является

Функция является примитивно рекурсивной, если она получается из набора исходных функций с помощью оператора: 1) рекурсии; 2) ограниченной минимизации; 3) подстановки - из перечисленного

Утверждение арифметики Пеано называется неразрешенным, если оно

Показал возможность существования универсальной вычислительной машины, способной выполнить любую эффективную процедуру

Частично вычислимая функция

Теория алгоритмов является частью

Выражение 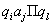является

Теорема Геделя о неполноте арифметики поколебала оптимистические надежды Гильберта на полное решение вопросов оснований математики с помощью

Каждая п.р.ф имеет число номеров

Всякая вычислимая функция является вычислимой по Тьюрингу согласно

Функция имеет гёделевский номер, равный

Если и рекурсия проводится по переменной , то функция равна

Машина Тьюринга есть совокупность компонент

В рекурсивно аксиоматизированной формальной системе, в которой все доказуемые утверждения истинны, существует истинное утверждение s, так что: 1) s недоказуемо; 2) Øs доказуемо - из перечисленного

Если и рекурсия проводится по , то функция равна

Если множество рекурсивно, то оно является ______ всюду определенной вычислимой функции

Если и рекурсия проводится по , то функция равна

Множество номеров несамоприменимых машин Тьюринга

Функция имеет гёделевский номер, равный

Если , то функция в рекуррентной формуле равна

Функция равна

Формализованный язык для однозначной записи алгоритмов называется

Множество, если его характеристический предикат является вычислимым, называется

Геделевский номер, равный 23, имеет функция

Усеченная разность равна

Теорема, связывающая рекурсивности множества с рекурсивной перечислимостью этого множества и его дополнения, называется теоремой