Линейная алгебра (курс 3)
По формулам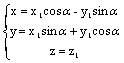 
производится преобразование координат
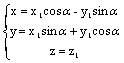производится преобразование координатпри параллельном сдвиге осей
при повороте вокруг оси Оz
при повороте вокруг оси Оу
при повороте вокруг оси Ох
В методе параллельных сечений рассматривают сечения данной поверхности
плоскостями вида x = h1, y = h2, z = h3 (hi - постоянные, i = 1, 2, 3)
плоскостями
только координатными плоскостями
параллельными плоскостями
Данная поверхность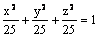 
является
являетсяэллипсоидом
сферой
конусом
эллиптическим цилиндром
Данная поверхность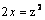 
является
являетсягиперболическим цилиндром
гиперболическим параболоидом
эллиптическим параболоидом
параболическим цилиндром
Вектор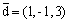 
является
являетсянаправляющим вектором прямой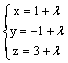 
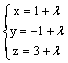
направляющим вектором прямой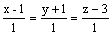 
нормальным вектором плоскости (x –1) – (y + 1) + (z – 3) = 0
нормальным вектором плоскости x - y + 3z - 2 = 0
Линейчатой поверхностью является
эллипсоид вращения
эллиптический параболоид
гиперболический параболоид
двухполостный гиперболоид
Данная поверхность 2х = у2 является
параболическим цилиндром
гиперболическим цилиндром
гиперболическим параболоидом
эллиптическим параболоидом
Данная поверхность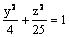 
является
являетсяэллипсоидом
конусом
гиперболическим цилиндром
эллиптическим цилиндром
Данная поверхность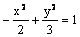 
является
являетсяоднополостным гиперболоидом
двухполостным гиперболоидом
эллиптическим цилиндром
гиперболическим цилиндром
Верны ли утверждения? А) Если вектор нормали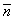 
плоскости a ортогонален направляющему вектору 
прямой L, то прямая L перпендикулярна плоскости a. В) Если уравнение плоскости имеет вид Ax + By + Cz = 0, то плоскость проходит через начало координат. Подберите правильный ответ
плоскости a ортогонален направляющему вектору 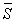прямой L, то прямая L перпендикулярна плоскости a. В) Если уравнение плоскости имеет вид Ax + By + Cz = 0, то плоскость проходит через начало координат. Подберите правильный ответА – да, В – да
А – да, В – нет
А – нет, В – да
А – нет, В – нет
Через точку (3, 3, 0) проходит
плоскость 3x + y + 5z + 13 = 0
прямая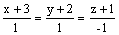 
прямая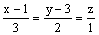 
плоскость x + y + z - 6 = 0
Вектор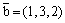 
является
являетсянаправляющим вектором прямой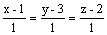 
нормальным вектором плоскости 4(x - 1) + 5(y - 3) - 7(z - 2) = 0
направляющим вектором прямой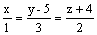 
нормальным вектором плоскости x + 3y + 2 = 0
Даны плоскости: а) 6x + 3y – 2z – 7 = 0; б) 2x + 6y – 3z + 21 = 0; в) 3x + 2y – 6z – 14 = 0.С увеличением расстояния от начала координат плоскости расположены в следующем порядке
б, в, а
а, б, в
а, в, б
в, б, а
Данная поверхность 2z =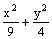 
является
являетсяэллиптическим цилиндром
Организующим
эллиптическим параболоидом
гиперболическим параболоидом
На плоскости Oxy уравнением прямой по точке M0(x0, y0) и направляющему вектору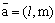 
является уравнение
является уравнение
l(x - x0) + m(y - y0) = 0
В пространстве Oxyz уравнением плоскости по точке M0(x0, y0, z0) и нормальному вектору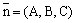 
является уравнение
является уравнениеA(x - x0) + B(y - y0) + C (z - z0) + D = 0
A(x - x0) + B(y - y0) + C (z - z0) = 0
Ax + By + Cz + D = 0
Уравнением 2x2 + y2 + 4z2 + 3 = 0 задается вырожденная поверхность второго порядка, представляющая собой
прямую
пустое множество
плоскость
точку
Вектор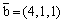 
является
являетсянормальным вектором плоскости 4x + y + 1 = 0
направляющим вектором прямой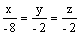 
направляющим вектором прямой 
нормальным вектором плоскости 2(x - 4) + 3(y - 1) + (z - 1) = 0
По формулам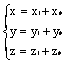 
производится преобразование координат
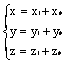производится преобразование координатпри повороте вокруг оси Оz
при повороте осей
при повороте вокруг оси Оу
при параллельном сдвиге осей
Вектор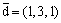 
является
являетсянаправляющим вектором прямой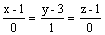 
нормальным вектором плоскости 2x + 6y + 2z = 0
направляющим вектором прямой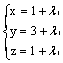 
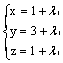
нормальным вектором плоскости x + 3y + 1 = 0
Данная поверхность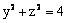 
является
являетсягиперболическим цилиндром
конусом
круговым цилиндром
эллипсоидом
Верны ли утверждения? А) Уравнение плоскости XOY имеет вид z = 0. В) Уравнение оси OX имеет вид x = a. Подберите правильный ответ
А – нет, В – да
А – да, В – нет
А – да, В – да
А – нет, В – нет
Уравнением x2 + y2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
прямую – ось OZ
точку
плоскость
пустое множество
Через точки М1(-2,0,0), М2(2,0,2) и М3(2,2,0) проходит плоскость
х-2у-z+1=0
х-3у-2z+1=0
х-2у-2z+2=0
х-2у-2z+4=0
Уравнением первой степени относительно x, y, z называется уравнение вида
Ax + By + Cz + D = 0
Ax + By + Cz + D = 0, A2 + B2 + C2 ¹ 0
Ax + By + Cz + D = 0, D ¹ 0
F(x, y, z) = 0
Вектор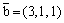 
параллелен прямой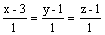 
перпендикулярен прямой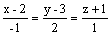 
перпендикулярен плоскости 7(x - 3) + 6(y - 1) + (z - 1) = 0
параллелен плоскости 6x + 2y + 2z -1 = 0
Вектор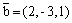 
перпендикулярен прямой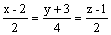 
перпендикулярен плоскости 4x - 6y + 2z - 1 = 0
параллелен прямой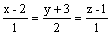 
параллелен плоскости 4(x - 2) + (y +3) + (z + 1) = 0
Вектор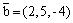 
является
являетсянормальным вектором плоскости 2x + 5y - 4 = 0
нормальным вектором плоскости (x - 2) + 3(y - 5) + 7(z + 4) = 0
направляющим вектором прямой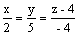 
направляющим вектором прямой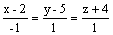 
Верны ли утверждения? А) Вектор 
, перпендикулярный данной прямой, называется направляющим вектором этой прямой. В) Если вектор нормали к плоскости a коллинеарен направляющему вектору прямой L, то плоскость a и прямая L параллельны. Подберите правильный ответ
, перпендикулярный данной прямой, называется направляющим вектором этой прямой. В) Если вектор нормали 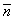к плоскости a коллинеарен направляющему вектору 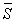прямой L, то плоскость a и прямая L параллельны. Подберите правильный ответА – нет, В – да
А – да, В – нет
А – нет, В – нет
А – да, В – да
Гиперболоид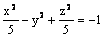 
является
являетсялинейчатой поверхностью
поверхностью вращения вокруг оси Ox
поверхностью вращения вокруг оси Oy
поверхностью вращения вокруг оси Oz
Прямая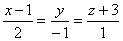 
и плоскость x + 2y + z+ 1 = 0 пересекаются в точке
и плоскость x + 2y + z+ 1 = 0 пересекаются в точкеМ(3, –1, –2)
М(2, –1, 1)
М(–1, 0, 3)
M(1, 0, –3)
Через точку (1, 4, 3) проходит
плоскость 4x - y - z = 0
плоскость 10y + z + 2= 0
прямая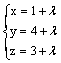 
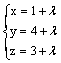
прямая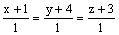 
Верны ли утверждения? А) Прямая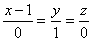 
перпендикулярна плоскости XOY. В) Прямая параллельна плоскости XOZ. Подберите правильный ответ
перпендикулярна плоскости XOY. В) Прямая 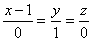параллельна плоскости XOZ. Подберите правильный ответА – нет, В – нет
А – нет, В – да
А – да, В – нет
А – да, В – да
На плоскости Oxy уравнение F(x, y) = 0 является уравнением данной линии, если
координаты (x, y) каждой точки, лежащей на линии, удовлетворяют этому уравнению
координаты каждой точки, не лежащей на линии, не удовлетворяют этому уравнению
x2 + y2 ¹ 0
координаты (x, y) каждой точки, лежащей на линии, удовлетворяют этому уравнению, а координаты (x, y) каждой точки, не лежащей на линии, этому уравнению не удовлетворяют
Верны ли утверждения? А) Пямая x = y = z перпендикулярна плоскости x + y + z = 3. В) Прямая x = y = z пересекает плоскость x + y + z = 3 в точке M(1, 1, 1). Подберите правильный ответ
А – нет, В – нет
А – нет, В – да
А – да, В – нет
А – да, В – да
В пространстве Oxyz прямая с направляющим вектором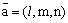 
, проходящая через точку M0(x0, y0, z0), задается следующим образом
, проходящая через точку M0(x0, y0, z0), задается следующим образомуравнением l(x - x0) + m(y - y0) + n (z - z0) = 0
уравнением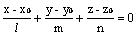 
каноническими уравнениями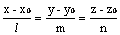 
параметрическими уравнениями 
Данная поверхность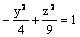 
является
являетсяэллиптическим цилиндром
однополостным гиперболоидом
гиперболическим цилиндром
двухполостным гиперболоидом
Данная поверхность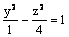 
является
являетсяэллиптическим цилиндром
гиперболическим цилиндром
двухполостным гиперболоидом
однополостным гиперболоидом
Данная поверхность 2у = х2 является
гиперболическим параболоидом
эллиптическим параболоидом
параболическим цилиндром
гиперболическим цилиндром
Уравнением y2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
точку
координатную плоскость Oxz
координатную плоскость Oyz
пустое множество
Уравнением z2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
координатную плоскость Oyz
координатную плоскость Oxy
пустое множество
точку