Геометрия (8 кл. БП)
В прямоугольном треугольнике ABC с прямым углом С и высотой CD: ВС = 6, АВ = 9. Найдите отрезки АD и DB 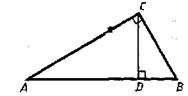

3
6
5
4
Примерами подобных фигур произвольной формы являются:
два прямоугольника, у которых две смежные стороны одного пропорциональны двум смежным сторонам другого
две фотографии одного и того же предмета, сделанные при разных увеличениях
два квадрата
две географические карты одного и того же района, выполненные в разных масштабах
В прямоугольном треугольнике ABC с прямым углом С и высотой CD: АС = 12, AD = 6. Найдите гипотенузу и другой катет 

18
2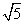
12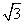
24
Высота прямоугольного треугольника, проведенная из вершины прямого угла:
есть среднее геометрическое для катетов
есть среднее пропорциональное для отрезков, на которые гипотенуза делится этой высотой
есть среднее арифметическое для катетов
делит гипотенузу на отрезки, пропорциональные прилегающим катетам
есть среднее арифметическое для отрезков, на которые гипотенуза делится этой высотой
Высота, проведенная из прямого угла С треугольника АВС, делит его гипотенузу на отрезки AD = 16 см и DВ = 4 см. Высота СD = _____ см 

Стороны треугольника АВС равны АВ = 8 см, ВС = 10 см и АС = 12 см, А1, В1, С1 – середины его сторон. Сторона А1С1 треугольника А1В1С1 равна _____ (число) см 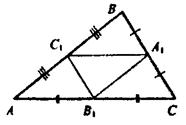

В прямоугольном треугольнике ABC с прямым углом С и высотой CD: AD = 25, DB = 16. Найдите катеты треугольника АВС 

4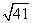
3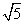
5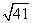
2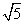
Высота, проведенная из прямого угла С треугольника АВС, делит его гипотенузу на отрезки AD = 18 см и DВ = 2 см. Высота СD = _____ см 

Верны ли определения? А) Середины сторон четырехугольника являются вершинами параллелограмма В) Четырехугольник есть ромб, если его вершинами являются середины сторон прямоугольника Подберите правильный ответ
А - да, В - да
А - нет, В - да
А - да, В - нет
А - нет, В - нет
Отрезок, соединяющий середины двух сторон треугольника, называется _____ линией треугольника