Математическая логика и теория алгоритмов
Совокупность исходных знаков, принятых за неделимые, и правил построения из них слов и словосочетаний без всякой связи с их возможной семантикой называется языком
формальным
программирования
логико-математическим
искусственным
Фразы, соединяемые функтором, называются
предложениями
аргументами
формульными
регулярными
Если 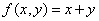 и рекурсия проводится по переменной
и рекурсия проводится по переменной 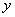 , то функция
, то функция 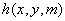 равна
равна
m+x
m+1
2+m
m+y
Не существует формальной системы арифметики, удовлетворяющей условиям полноты и противоречивости согласно
теории Гильберта
тезису Черча
теореме Поста
теореме Геделя
Множество всевозможных осмысленных утверждений языка является
рекурсивным
креативным
неперечислимым
рекурсивно перечислимым
Если множество неперечислимо, то оно _______ областью определения и ______ множеством значений всюду определенной вычислимой функции
не может быть, не может быть
может быть, не может быть
может быть, может быть
не может быть, может быть
Лента машины Тьюринга
считывается в обе стороны
должна быть только одномерной
может быть многомерной
не содержит результаты вычислений
Частично вычислимая функция
это частный случай вычислимой
вычисляется с ограниченной точностью
не везде совпадает с вычислимой
может быть продолжена до вычислимой
В рекурсивно аксиоматизированной формальной системе, в которой все доказуемые утверждения истинны, существует истинное утверждение s, так что: 1) s опровержимо; 2) Øs опровержимо
1
1 и 2
ни 1, ни 2
2
Ограничения, накладываемые на базовые термы лингвистической переменной
упорядоченность, полнота и согласованность, непрерывность, типичность, нормальность, ограниченность
нормальность, ограниченность
упорядоченность, полнота и согласованность, нормальность, ограниченность
полнота исогласованность, нормальность, ограниченность
Функция, равная единице тогда и только тогда, когда предикат истинен, называется
вычислимой
частично рекурсивной
характеристической
примитивно вычислимой
Функция, вычислимая по Тьюрингу, является
общерекурсивной
частично рекурсивной
примитивно рекурсивной
характеристической
Требование, предъявляемое к синтаксическому правилу (т. е. к любой фразе, построенной с использованием базовых термов и терминальных символов)
ограниченности
замкнутости
разомкнутости
упорядоченности
Атомарная формула или ее отрицание называется
конъюктом
предикатом
литерой
дизъюнктом
Если 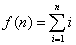 , то функция
, то функция 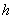 (n,m) в рекуррентной формуле равна
(n,m) в рекуррентной формуле равна
m+n+1
m+n-1
(m+n)/2
2m
Умозаключения - элементарные рассуждения, в которых из одного или нескольких суждений получается еще одно суждение, называемое
посылками
заключением
суждением
экспликацией
Примером семантического парадокса может(-гут) служить
парадокс лжеца
парадокс Рассела
парадоксы лжеца и Берри
парадокс Берри
Главное отличие аксиоматического подхода от конструктивного состоит в том, что аксиоматический подход опирается
только на структуру модели
только на формализм знаков
в меньшей степени на формализм знаков, чем на структуру модели
в большей степени на формализм знаков, чем на структуру модели
Если невозможно дать какие-либо количественные оценки, но имеются некоторые эталонные объекты, описывать другие объекты предполагается с помощью
нечисловой лингвистической переменной
числовой лингвистической переменной
числовой лингвистической постоянной
нечисловой лингвистической постоянной
Наиболее часто на практике используется опрос экспертов
индивидуальный прямой
групповой прямой
индивидуальный косвенный
групповой косвенный
Формализованный язык для однозначной записи алгоритмов называется
алгоритмическим языком
метаязыком языком
автоматным языком
регулярным языком
Если множество нерекурсивно, то оно _______ областью определения и ______ множеством значений всюду определенной вычислимой функции
может быть, не может быть
не может быть, может быть
не может быть, не может быть
может быть, может быть
Концептуальное отличие нечеткой логики от классической заключается в том, что она оперирует
не только значениями "истина" и "ложь", но и промежуточными значениями
только значениями "ложь"
только значениями "истина" и "ложь"
только промежуточными значениями
В любой рекурсивно аксиоматизированной формальной системе множество доказуемых утверждений
нерекурсивно
неперечислимо
рекурсивно перечислимо
разрешимо
Любая неразрешимая алгоритмическая проблема дает пример множества
несчетного
неперечислимого
невычислимого
неразрешимого
Множество, если его характеристический предикат является вычислимым, называется
рекурсивно перечислимым
эффективным
вычислимым
рекурсивным
Логика, содержащая понятия необходимости, возможности или родственные этим понятия, называется
высказываний
модальной
Буля
математической
Логическая связка 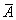 , где А - высказывание, обозначает
, где А - высказывание, обозначает
конъюнкцию
импликацию
отрицание
дополнение
В логических парадоксах используются только понятия теории
множеств
парадоксов
аксиоматической
дедуктивной
Аксиоматическая теория возникла в связи со стремлением уточнить методы теории множеств таким образом, чтобы избежать парадоксов
логических
любых
семантических
эпистемологических
Если множество рекурсивно, то оно является ______ всюду определенной вычислимой функции
ни множеством значений, ни областью определения
только множеством значений
только областью определения
множеством значений и областью определения
Язык, на котором описывается другой язык, называется
автоматным языком
формальной системой
формулой языка Ъ
метаязыком
Множество истинных утверждений
носит название системы аксиом
не выводится из системы аксиом
перечисляет все системы аксиом
выводится из системы аксиом
Дополнение к области определения некоторой вычислимой функции _________ рекурсивно перечислимым
должно быть
может не быть
не может быть
разъединено с
Язык логики предикатов является расширением языка
логики высказываний
формальной логики
математической логики
нечеткой логики
Машина Тьюринга есть совокупность компонент
трех
двух
пяти
четырех
Каждый язык первого порядка задается своим набором из
двух множества = (Сnst, Fn), где Cnst - множество констант, Fn - множество функциональных символов
одного множества = (Сnst) , где Cnst - множество констант
трех множеств = (Сnst, Fn, Pr), где Cnst - множество констант, Fn - множество функциональных символов, Pr - множество предикатных символов
двух множеств = (Fn, Pr), где Fn - множество функциональных символов, Pr - множество предикатных символов
Логическая связка дизъюнкция высказываний А и В обозначается как
А 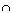 В
В
А 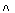 В
В
А 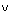 В
В
А 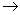 В
В
Функция, определяемая как число шагов в вычислении машиной Тьюринга, называется
характеристической
временным ресурсом
длиной программы
геделевским номером
Если A и B - рекурсивные множества, то рекурсивны также множества I.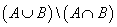 II.
II.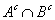 III.
III.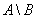
только I и II
I, II и III
только I и III
только II