Элементы комбинаторики. Теория графов и сетей. Теория кодирования. Конечные автоматы. Теория алгоритмов и вычислимых функций
В коде алфавита {a: 001, b: 01, c: 10} кодом сообщения сасb служит
010011001
100011001
100101001
101000101
Число слов длины 2 в алфавите {a, b, c, d, e} равно
32
25
20
120
Вычисление попарных расстояний Хэмминга для кодовых слов алфавита V = {a, b, c} a: 10100, b: 11001, c: 01101 b: 11011, c: 01101 a: 10111 (второй ряд записан под первым для удобства вычислений) показывает, что кодовое расстояние данного кода равно
2
3
5
4
Степени вершин в графе переходов (без склеивания дуг) автомата с входным алфавитом {a, b, c, d, e, f}, выходным алфавитом {a, d, е, g, h} и 4 состояниями равны
4
5
6
24
Число ребер в остове полного двудольного графа К6, 9 равно _____ .
Максимальное число абонентов, которых можно обеспечить 4-значными телефонными номерами, составляет
10000
256
24
16
В графе G последовательность ребер представляет собой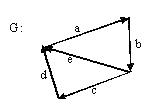 
[d c b]
контур
[d a b]
путь
[c d a b]
цепь
Цикломатическое число графа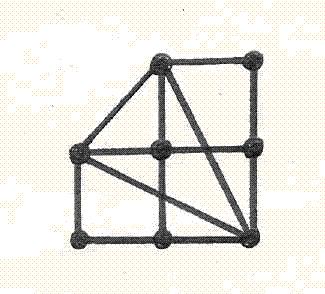 
8
6
12
10
Число ребер в полном двудольном графе К3,5 равно _____ .
В графе G последовательность ребер представляет собой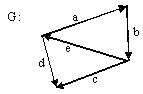 
[b e a]
путь
[d a b]
цепь
[b e d]
контур
Префиксными кодами являются
{a: 01, b: 101, c: 110}
{a: 001, b: 01, c: 101, d: 10}
{a: 001, b: 10, c: 110, d: 111}
{a: 01, b: 011, c: 1010, d: 11}
Число слов длины 3 в алфавите {a, b, c, d, e} равно
60
120
243
125
Укажите соответствие между сообщениями в алфавите {А, В, С} и их кодами при побуквенном кодировании [А: 0, В: 10, С: 11]
BСА
01011
CАВ
11010
AВС
10110
Матрица 
представляет собой матрицу соседства вершин неориентированного графа
представляет собой матрицу соседства вершин неориентированного графа
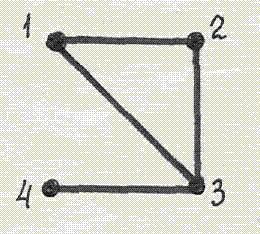
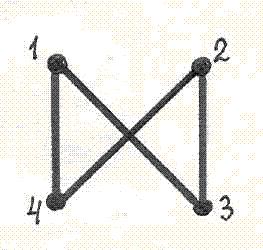
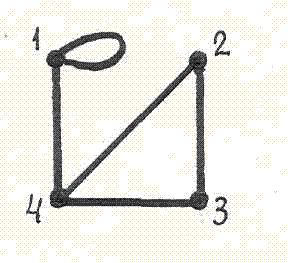
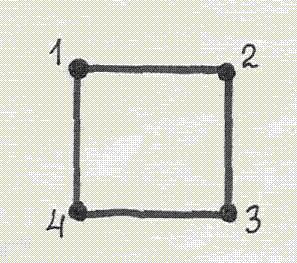
Число слов длины 4 в алфавите {a, b, c, d, e} вычисляется по формуле
4554C54
C45
Число различных 4-значных чисел, которые можно составить из всех цифр числа 9471, равно
64
24
16
256
В коде алфавита {a: 011, b: 01, c: 10} последовательность 100110101 служит кодом сообщения
cabb
cbaa
baca
cacb
Расстояние между вершинами А и В в графе с заданными длинами ребер равно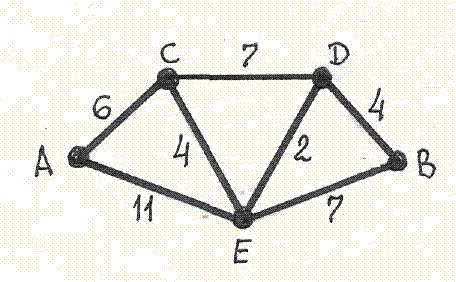 
4
16
18
2
Без разделителей можно использовать код алфавита
{a: 01, b: 10, c: 100}
{a: 01, b: 11, c: 101}
{a: 0, b: 100, c: 110}
{a: 00, b: 01, c: 010}
Число вершин в графе переходов автомата с входным алфавитом {a, b, c}, выходным алфавитом {a, c, d} и 5 состояниями равно
5
15
45
9
При передаче сообщения 0011001 произошла ошибка вида L ® 0 между 4-м и 5-м разрядами. На приемнике получено сообщение ___________.
В данной сети из полюса α в полюс δ ведут ___ различных элементарных путей (ответ – целое число).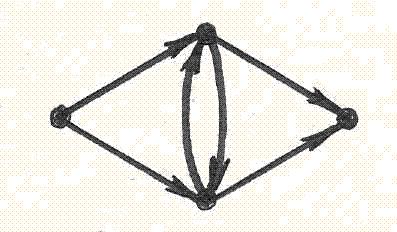 
Цикломатическое число графа равно _____ .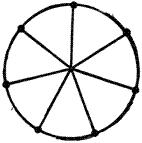 
Укажите соответствие между комбинаторными конфигурациями и формулами для их пересчета:
четырехэлементные подмножества множества из 9 элементов
49слова длины 3 из всех букв алфавита {a, b, c}
Р3
слова длины 9 в алфавите {a, b, c, d}
С94
Требуется кодировать равномерным двоичным кодом 280 различных объектов. Код должен иметь длину не менее _____ .
Число ребер в полном графе K7 равно _____ .
При передаче сообщения 00110111 произошла ошибка типа {1 ® 0, 0 ® 1} во 5-м и 6-м разрядах. На приемнике получено сообщение _________.
Число различных 4-значных нечетных чисел, которые можно составить из всех цифр числа 6534, равно
12
18
6
24
Число различных 4-значных нечетных чисел, которые можно составить из всех цифр числа 4638, вычисляется по формуле
3 ∙ 3!
3!
4! / 3
4!
Цикломатическое число графа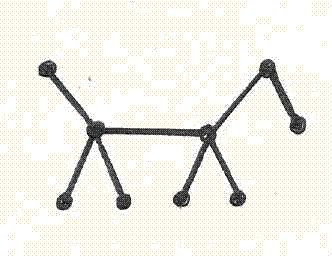 
2
0
7
8
Число слов длины 3 в алфавите {a, b, c, d} вычисляется по формуле
A43
C43
Укажите соответствие между графами и их цикломатическими числами:
0
2
1
Стоимость S кода алфавита с заданными частотами букв a: 01 0.5 b: 1010 0.3 c: 110 0.2 равна
3.0
2.8
1.0
3.2
Кодовый замок имеет 10 клавиш с цифрами 0, 1, 2,..., 9. Для открывания двери нужно одновременно нажать 3 клавиши. Число всевозможных кодов такого замка равно
310
100
120
720
При передаче сообщения 1010101 произошла ошибка вида 0 ® L в 6-ом разряде. На приемнике получено сообщение _________.
Число различных элементарных цепей [a, d] в данной сети равно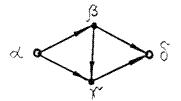 
2
4
5
3
Число различных 4-значных четных чисел, которые можно составить из всех цифр числа 6853, вычисляется по формуле
2 ∙ 3!
3 ∙ 3!
4!
3!
Кратчайший путь [a, b] в сети имеет длину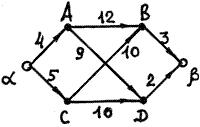 
15
19
17
18
При правильной раскраске полного графа К6 минимальное число красок равно
15
5
2
6
Число различных 4-значных нечетных чисел, которые можно составить из всех цифр числа 6853, вычисляется по формуле
3 ∙ 3!
3!
4!
2 ∙ 3!
Значение суперпозиции I1 (N(6), Z(4)) исходных п/р функций и констант 6, 4 равно ____ .
Значение суперпозиции N(I1 (3, Z(3))) исходных п/р функций и констант 3, 3 равно ____ .
При правильной раскраске полного графа К5 минимальное число красок равно
10
2
5
6
Число различных 4-значных нечетных чисел, которые можно составить из всех цифр числа 4836, вычисляется по формуле
Р4
3!
А43
А33
При правильной раскраске графа (т. е. соседние вершины – разного цвета)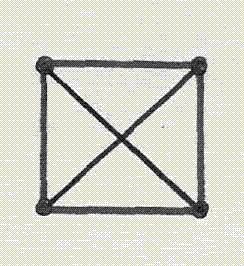 
минимальное число красок равно
минимальное число красок равно4
1
3
2
В данной сети из полюса α в полюс γ ведут ___ различных элементарных цепей (ответ – целое число).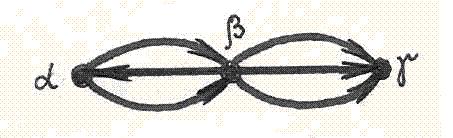 
Число различных 6-значных чисел, которые можно составить из всех цифр числа 285419, вычисляется по формуле
А66
6!
В графе Е3 (трехмерном единичном кубе) ___ различных элементарных цепей длины 3 связывают вершины (0 0 0) и (1 1 1) (ответ – целое число).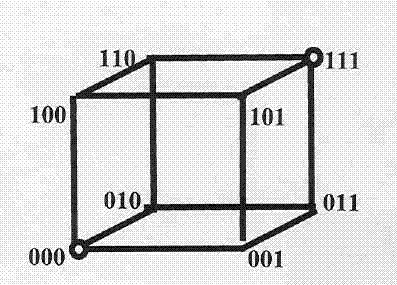 
Число размещений с повторениями из 4 элементов по 2 равно _____ .
Укажите соответствие между сообщениями в алфавите {А, В, С} и их кодами при побуквенном кодировании [А: 0, В: 10, С: 11]
CВА
10011
AСВ
01110
BАС
11100