Математическая логика и теория алгоритмов
Осмысленные конечные последовательности символов из алфавита L называются
программой
словарем
командами
утверждениями
________- это раздел математики, объектом изучения которого являются математические абстракции программ, выполненных на определенных алгоритмических языках и обладающих определенной информационной и логической структурой
математическое программирование
неевклидова геометрия
теоретическое программирование
математический анализ
Логика высказываний и логика предикатов базируются уже на
аксиоматическом подходе
отношении эквивалентности
отношении эквивалентности и отношении порядка
отношении порядка
При аксиоматическом подходе, как методе доказательства, осуществляется движение мысли от
общего к частному
общего к общему
частного к общему
частного к частному
Символы _____________ входят в алфавит формального логического языка
Функция, вычислимая по Тьюрингу, является
частично рекурсивной
примитивно рекурсивной
характеристической
общерекурсивной
Логика интересуется в первую очередь
умозаключением
содержанием доводов
формой
рассуждением
Язык логики предикатов является расширением языка
нечеткой логики
формальной логики
логики высказываний
математической логики
Система, в которой знаки не функционируют независимо друг от друга, а образуют систему, правила которой определяют закономерности их построения, осмысления и употребления, называется
языковая
формальная
знаковая
языковая, знаковая
Построить любую правильную цепочку символов позволяет формальная грамматика, которая называется грамматикой
нормальной
порождающей
регулярной
автоматной
Запись _________ означает: выражение «множество А содержится в множестве В»
А Ì В
А / В
А 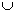 В
В
А 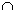 В
В
Функция 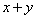 является: 1) частично вычислимой; 2) примитивно рекурсивной; 3) частично рекурсивной
является: 1) частично вычислимой; 2) примитивно рекурсивной; 3) частично рекурсивной
1 и 2
1
1 и 3
2 и 3
Всякая непротиворечивая система арифметики с рекурсивной системой аксиом
является замкнутой
совпадает с системой Пеано
не может быть полной
должна быть полной
Нечеткое множество, высота которого равна 1, называется
нормальным
субнормальным
единичным
одиночным
Множество всевозможных осмысленных утверждений языка является
креативным
неперечислимым
рекурсивно перечислимым
рекурсивным
Функция 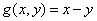 является
является
вычислимой
общерекурсивной
частично вычислимой
рекурсивной
Базовая единица языка, обладающая определенной для данного языка синтаксической и смысловой законченностью и выражающая утверждение, называется
слово
подмножество
предложение
выражение
Множество всех истинных утверждений языка L является
неразрешимым и неперечислимым
неразрешимым, но перечислимым
разрешимым и перечислимым
разрешимым, но неперечислимым
Всякое непустое ______ множество является _________ некоторой всюду определенной вычислимой функции
рекурсивное, областью определения
рекурсивно перечислимое, множеством значений
продуктивное, множеством значений
креативное, областью определения
Истинная при всех интерпретациях формула называется
общезначимой
неразрешимой
разрешимой
выводимой
Внутренним алфавитом машины Тьюринга называется
символы, записанные на ленте
множество команд машины
множество конфигураций машины
множеством состояний машины
Запись __________ обозначает пересечение множеств А и В
А 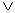 В
В
А Ç В
А 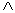 В
В
А È В
Если множество является множеством значений некоторой вычислимой функции, то оно называется
вычислимым
эффективным
рекурсивно перечислимым
разрешимым
Выражение 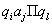 является
является
командой
исходной ситуацией
машиной Тьюринга
элементом алфавита
В рекурсивно аксиоматизированной формальной системе, в которой все доказуемые утверждения истинны, существует истинное утверждение s, так что: 1) s недоказуемо; 2) Øs доказуемо - из перечисленного
1 и 2
1
ни 1, ни 2
2
Множество номеров самоприменимых машин Тьюринга
рекурсивно перечислимо и разрешимо
рекурсивно перечислимо, но не разрешимо
ни перечислимо, ни разрешимо
неперечислимо, но разрешимо
В XIX столетии оживился интерес к логике под влиянием открытия
теории абстрактных множеств
математического анализа
неевклидовых геометрий
теории парадоксов
Метод парных сравнений, лежит в основе метода анализа иерархий, предложенного
М. Саати
Кантором
Бурали-Форти
Расселом
Множество номеров несамоприменимых машин Тьюринга
неперечислимо
неразрешимо
рекурсивно перечислимо
рекурсивно
Законченная последовательность знаков определенной длины, воспринимаемая как элемент обработки с определенным семантическим содержанием, называется
язык
слово
выражение
предложение
Если характеристический предикат множества является вычислимым, такое множество называется
рекурсивным
рекурсивно перечислимым
вычислимым
эффективным
Требование _________предъявляется к термам лингвистической переменной
не отрицательности
не противоречивости
истинности
упорядоченности
Термин «некоторые х» или «существует хотя бы одно значение х» обозначается через
А х
Е х
__________ называется выражением
исходная ситуация
набор команд
конечная последовательность символов
внутреннее состояние
Запись ______________ обозначает логическую связку эквивалентность
В ~ А
А 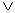 В
В
Единственным неопределимым отношением в системе Пеано является выражение
Каждый язык первого порядка задается своим набором из
двух множества = (Сnst, Fn), где Cnst - множество констант, Fn - множество функциональных символов
двух множеств = (Fn, Pr), где Fn - множество функциональных символов, Pr - множество предикатных символов
одного множества = (Сnst) , где Cnst - множество констант
трех множеств = (Сnst, Fn, Pr), где Cnst - множество констант, Fn - множество функциональных символов, Pr - множество предикатных символов
Когда 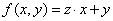 и рекурсия проводится по переменной
и рекурсия проводится по переменной 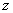 , функция
, функция 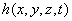 равна
равна
ty
t+x+y+z
Аксиоматическая теория возникла в связи со стремлением уточнить методы теории множеств таким образом, чтобы избежать парадоксов
логических
любых
эпистемологических
семантических