Математика (курс 10)
Интерполяционный многочлен второй степени вида 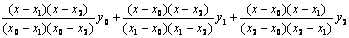 называется интерполяционным многочленом
называется интерполяционным многочленом
Чебышева
Ньютона
Лагранжа
Гаусса
Погрешность метода трапеций на всем отрезке интегрирования имеет порядок k , равный
1
2
3
1,5
Заданы уравнения: 1) 2sin x = cos2 x ; 2) lnx = x ; 3) x = e-x ; 4) x2 = cosx +1 ; 5) ex + x = x . Вид удобный для итераций, имеют уравнения
2, 3 и 5
1 и 2
3, 4 и 5
2, 4 и 5
Дана система 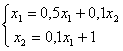 и задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение
и задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение
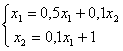 и задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение
и задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение(0,6 ; 1)
(0,1 ; 1,06)
(0,6 ; 1,1)
(0,6 ; 1,06)
Даны уравнения: 1) x = 2sin x ; 2) x = sin 0,5x ; 3) x = 5cos x ; 4) x = 3cos 0,1x Метод простой итерации будет сходиться для уравнений
2 и3
1, 3 и 4
2 и 4
1 и 2
Метод Зейделя для системы линейных уравнений 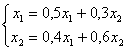
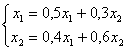
сходится при x1 = 0 , x2 = 0
сходится при любом начальном приближении
расходится при любом начальном приближении
приведет к зацикливанию
В таблично заданной функции производная в точке 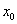 вычислена с использованием шагов h и 2h . Получены величины
вычислена с использованием шагов h и 2h . Получены величины 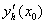 = 0,8 и
= 0,8 и 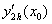 = 0,65. Погрешность формулы для вычисления производных имеет порядок
= 0,65. Погрешность формулы для вычисления производных имеет порядок 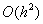 . Тогда уточненное значение производной
. Тогда уточненное значение производной 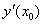 по методу Рунге равно
по методу Рунге равно
0,75
0,87
0,7
0,805
Порядок сходимости метода простой итераций для одного нелинейного уравнения в общем случае равен
0
2
1
0,5
Выбор начального приближения на сходимость или расходимость метода Зейделя при решении систем линейных уравнений
не влияет
влияет, если матрица не является верхней треугольной
влияет всегда
влияет, если матрица не симметричная
Сплайн - интерполяция - это:
кусочно-постоянная функция
интерполяция, использующая тригонометрические функции
кусочно-многочленная интерполяция
интерполяция, использующая показательные функции
Дано уравнение x = sinx + 1 и начальное приближение x0 = π ⁄ 2 . Первое приближение x1 метода простой итераций равно
2
1
π
0
Достаточным условием сходимости метода Ньютона для уравнения F( x ) = 0 будет выполнение условия
Прямой ход метода Гаусса сводит линейную систему уравнений к виду:
с верхней треугольной матрицей
с трехдиагональной матрицей
с симметричной матрицей
с диагональной матрицей
Квадратурная формула метода трапеций на всем интервале интегрирования имеет порядок погрешности
1
0
2
3
Матрица A= 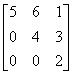 называется
называется
 называется
называетсяверхней треугольной
ленточной
трехдиагональной
треугольной
Один шаг метода половинного деления для уравнения x2 − 2 = 0 для начального отрезка [0; 2] дает следующий отрезок
[0,5 ; 1]
[0; 1]
[1,5 ; 2]
[1; 2]
Формула метода трапеций для вычисления определенного интеграла по сравнению с формулой метода Симпсона
имеет одинаковую точность
имеет для гладких функций меньшую точность
имеет для гладких функций большую точность
имеет для любых функций большую точность
Аппроксимация называется точечной, если:
аппроксимирующая функция φ(x) вычисляется по значениям функции и ее производных в одной точке
аппроксимирующая функция φ(x) строится на дискретном множестве точек
значения аппроксимирующей и аппроксимируемой функции совпадают в граничных точках отрезка
для построения аппроксимирующей функции φ(x) используются точки, выбранные случайным образом
Задано нелинейное уравнение F( x ) = 0 , для которого известно, что 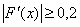 . Тогда точность вычисления корня
. Тогда точность вычисления корня 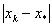 на k - ой итерации ( x* − точное значение корня) будет меньше, чем
на k - ой итерации ( x* − точное значение корня) будет меньше, чем
0,2 F′(xk)
0,2 F( xk )
( 0,2 )k
Для таблично заданной функции 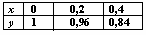 Результат линейной интерполяции при x=0.1 дает значение
Результат линейной интерполяции при x=0.1 дает значение
1,02
0,98
0,95
0,97
Условие сходимости метода итераций для нелинейного уравнения x = φ( x ) заключается в том, что
Подынтегральная функция y = f(x) задана таблично 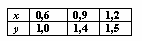 Вычисление интеграла
Вычисление интеграла 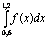 методом Симпсона при h = 0,3 дает значение равное:
методом Симпсона при h = 0,3 дает значение равное:
0,81
0,793333
0,7
0,84
Даны линейные системы 1)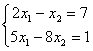 2)
2)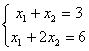 3)
3)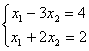 4)
4)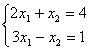 Свойством диагонального преобладания обладают системы
Свойством диагонального преобладания обладают системы
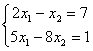 2)
2)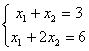 3)
3)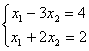 4)
4)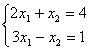 Свойством диагонального преобладания обладают системы
Свойством диагонального преобладания обладают системы1, 3 и 4
3 и 4
1 и 4
1 и 2
Отделить корни при решении нелинейного уравнения F( x ) = 0 это значит:
расставить корни в порядке их возрастания
отделить положительные корни от отрицательных
для каждого корня указать область притяжения
для каждого корня указать интервал, в котором он будет единственным
Задано нелинейное уравнение вида x3 + 2x - 1 =0 и отрезок [ 0 ; 1 ] , на котором находится корень . Один шаг метода половинного деления дает отрезок
[ 0,25 ; 0,75 ]
[ 0 ; 0,5 ]
[ 0,25 ; 1 ]
[ 0,5 ; 1 ]
Задана табличная функция y = f(x) 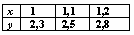 Первая производная на левом конце
Первая производная на левом конце 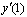 с погрешностью
с погрешностью 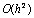 равна
равна
2,5
2
1,5
1,7
Задана линейная система 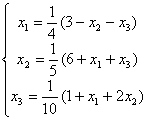 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 , один шаг метода Зейделя { x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 , один шаг метода Зейделя { x1(1), x2(1), x3(1)} будет равен
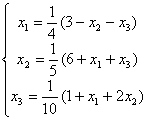 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 , один шаг метода Зейделя { x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 , один шаг метода Зейделя { x1(1), x2(1), x3(1)} будет равен{0,75 ; 1,2; 0,445 }
{0,75 ; 1,2; 0,1 }
{0,75 ; 1,35 ; 0,05 }
{ 0,75 ; 1,35 ; 0,445 }
Число 125,7 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление
0,1257∙103
125,7
0,01257∙104
1,257∙102
Подынтегральная функция y = f(x) задана таблично 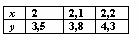 Вычисление интеграла
Вычисление интеграла 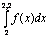 методом трапеций при h = 0,2 дает значение равное:
методом трапеций при h = 0,2 дает значение равное:
1,02
0,79
0,78
0,68
Дано уравнение x3 - x = 0 и начальное приближение x0 = 1. Результат одного шага метода Ньютона равен
x1 = −1
x1 = 1
x1 = 2
x1 = 0,5
Заданы системы линейных уравнений 1) 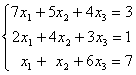 2)
2) 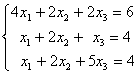 3)
3) 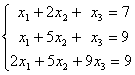 Свойством диагонального преобладания обладают матрицы систем
Свойством диагонального преобладания обладают матрицы систем
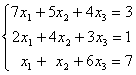 2)
2) 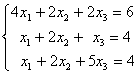 3)
3) 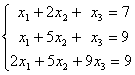 Свойством диагонального преобладания обладают матрицы систем
Свойством диагонального преобладания обладают матрицы систем1
2 и 3
1 и 2
2
Алгоритм называется неустойчивым, если
большие изменения в исходных данных не изменяют окончательный результат
малые изменения исходных данных не изменяют окончательный результат
большие изменения в исходных данных приводят к малому изменению результата
малые изменения исходных данных и погрешности округления приводят к значительному изменению окончательных результатов
Матрица линейной системы 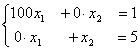 является
является
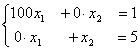 является
являетсядиагональной
единичной
треугольной
трехдиагональной
Задана табличная функция y = f(x) 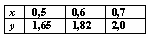 Первая производная на правом конце
Первая производная на правом конце 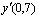 с погрешностью
с погрешностью 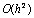 равна
равна
1,85
2
1,8
1,92
Задана система уравнений 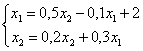 Для заданного начального приближения x1(0) = 0 ;x2(0) = 1, первый шаг метода Зейделя дает следующие значения первого приближения { x1(1) , x2(1) }
Для заданного начального приближения x1(0) = 0 ;x2(0) = 1, первый шаг метода Зейделя дает следующие значения первого приближения { x1(1) , x2(1) }
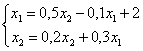 Для заданного начального приближения x1(0) = 0 ;x2(0) = 1, первый шаг метода Зейделя дает следующие значения первого приближения { x1(1) , x2(1) }
Для заданного начального приближения x1(0) = 0 ;x2(0) = 1, первый шаг метода Зейделя дает следующие значения первого приближения { x1(1) , x2(1) }{ 1,5 ; 0,2 }
{ 2,5 ; 0,95 }
{ 2 ; 0 }
{ 2,5 ; 0,2 }
Приближенное значение интеграла, вычисленные методом трапеций с шагами h и h∕2 равны 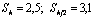 . Погрешность метода имеет вид
. Погрешность метода имеет вид 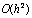 . Уточненное значение интеграла по методу Рунге равно:
. Уточненное значение интеграла по методу Рунге равно:
3,3
3,5
2,9
3,15
Результат вычисления интеграла 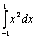 методом трапеций с разбиением на два интервала (h = 1) равен
методом трапеций с разбиением на два интервала (h = 1) равен
1
0,25
0,666667
0,6
Даны линейные системы 1)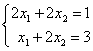 2)
2)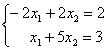 3)
3)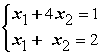 )
)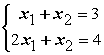 Свойством диагонального преобладания обладают системы
Свойством диагонального преобладания обладают системы
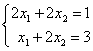 2)
2)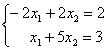 3)
3)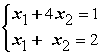 )
)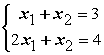 Свойством диагонального преобладания обладают системы
Свойством диагонального преобладания обладают системы1, 4
2, 3, 4
2, 4
1, 2
Если на отрезке [ a , b ] функция F( x ) непрерывна, F( a ) ∙ F( b ) < 0, то метод половинного деления для уравнения F( x ) = 0 сходится
если F( x ) ∙ F′( x ) > 0
всегда
при 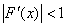
при F′( x )> 0
Подынтегральная функция y = f(x) задана таблично 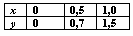 Вычисление интеграла
Вычисление интеграла 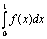 методом трапеций при h = 0,5 дает значение равное:
методом трапеций при h = 0,5 дает значение равное:
0,725
0,7
0,815
0,75
Для обратного хода метода Гаусса подготовлены следующие системы уравнений 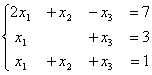
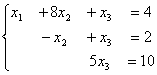
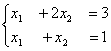
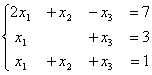
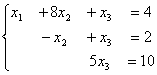
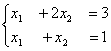
3
никакая
1 и 2
2
Дана система 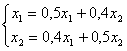 Первое приближение для метода Зейделя с начальным приближением ( 0,1 ; 0,2 ) будет равно
Первое приближение для метода Зейделя с начальным приближением ( 0,1 ; 0,2 ) будет равно
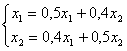 Первое приближение для метода Зейделя с начальным приближением ( 0,1 ; 0,2 ) будет равно
Первое приближение для метода Зейделя с начальным приближением ( 0,1 ; 0,2 ) будет равно( 0,14 ; 0,13 )
( 0,5 ; 0,4 )
( 0,13 ; 0,152 )
( 0,9 ; 0,9 )