Алгебра и начала анализа (11 класс)
Верны ли утверждения? А) Если при прямолинейном движении путь s, пройденный точкой, есть функция от времени t, т.е. s = f(t), то скорость точки есть производная от пути по времени, т.е. v(t)=f ’(t) В) Если в точке х0 к графику функции y = f(x) проведена касательная, то число f '(x0) есть тангенс угла α между этой касательной и положительным направлением оси Ох, т.е. f '(x0)= tgα Подберите правильный ответ
А - да, В - да
А - нет, В - да
А - нет, В - нет
А - да, В - нет
Верны ли утверждения? А) Если функции u(x) и v(x) имеют производные в точке x, то их произведение f(x) = u(x) × v(x) также имеет в этой точке производную, равную f ’(x)=u'(x)×v(x)+u(x)×v'(x) В) Если функции u(x) и v(x) имеют в точке x производные, то их разность f(x) = u(x) - v(x) также имеет в этой точке производную, равную f '(x) = u'(x) - v' (x) Подберите правильный ответ
А - нет, В - да
А - нет, В - нет
А - да, В - нет
А - да, В - да
Установите соответствие
(cos x)’
cos x
(tg x)’
(ctg x)’
(sin x)’
-sin x
Четная функция - функция y = f(x) с областью определения X, для которой для любого х Î Х число (-x) Î Х и справедливо равенство
f(-x) = -4f(x)
f(-x) = f(x)
f(-x) = -f(x)
f(-x) = -2f(x)
Пусть на промежутке I с концами а и b функция f(x) непрерывна вместе со своими первой и второй производными и х0 - единственная ее критическая точка на интервале (а; b). Тогда если f'(х0) = 0 и f"(x0)>0, то точка х0 есть точка ___________ на промежутке I
Вторая производная функции: f(x) = sin x равна f "(x) = ____________
cos x
sin x
-sin x
-cos x
Установите соответствие
(sin x)‘
-cos x
(sin x)(4)
-sin x
(sin x)‘‘
sin x
(sin x)‘‘‘
cos x
Третья производная функции: f(x) = sin x равна f ‘’’(x) = ____________
-cos x
sin x
cos x
-sin x
Верны ли утверждения? А) Если функция F(x) есть какая-либо первообразная функции f(x) на интервале (а; b), то всевозможные первообразные функции f(x) на этом интервале выражаются формулой F(x) + С, где вместо С можно подставить любое число В) Неопределенным интегралом от непрерывной на интервале (а; b) функции f(x) называют любую ее первообразную функцию Подберите правильный ответ
А - да, В - нет
А - нет, В - нет
А - нет, В - да
А - да, В - да
Тангенс угла наклона касательной к графику функции f(x) = 0,5х2-2х + 4 в точке с абсциссой x = 0 равен ______
4
3
2
-2
Разность значений функции в точках x+Dх и x называют приращением ____________
независимой переменной
производной
аргумента
функции
Максимум функции f(x) = |x – 2| на интервале (0; 6) _______
= 4
= 2
= 0
не существует
Вертикальная асимптота - асимптота, имеющая уравнение ______________
x = а, где а Î R
y = -x
y = x
y = а, где а Î R
________ производная функции f(x) - производная функции f ’(x) (если она существует)
_______________ функции f на отрезке [а; b] – операция, при помощи которой по данной функции y = f(x), заданной на отрезке [а; b], определяется число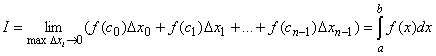 
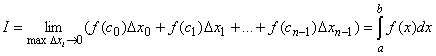
Пусть функция y = f(x) непрерывна на промежутке I и имеет производную f ’(x) в каждой точке внутри промежутка I. Тогда если f ’(x) = 0 для всех x внутри промежутка I, то функция y = f(x) ___________ на промежутке I
возрастает
убывает
есть постоянная (константа)
имеет значение, равное 0
Для любого действительного x ≠ pk, kÎZ, справедлива формула: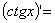 
________
________
Производная функции f(x) = 3x4 + 2x2 + c в любой точке x равна ___
12х3 + 4x + с
12х3 + 4x
7х3 + 4x
12x3
Производная функции f(x) = sin x в точке с абсциссой x =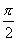 
равна ___
равна ___0,5
1
0
-1
______________ функции - операция нахождения предела отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю
Неопределенный интеграл от функции f(x) обозначают так: _____________
Верны ли утверждения? А) При а > 0 и а ≠ 1, для любого xÎR справедлива формула: (ах)' = ах-1 lg а В) (ех)' =ех Подберите правильный ответ
А - нет, В - да
А - нет, В - нет
А - да, В - нет
А - да, В - да
Пусть функция f(x) непрерывна на отрезке [а; b] и пусть F(x) есть какая-либо ее первообразная. Тогда справедливо равенство _________________
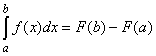
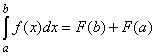
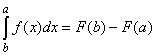
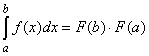
Производная функции f(x) = x2 + 4x в точке с абсциссой x = 1 равна ___
6
1
5
2
Верны ли утверждения? А) Наибольшее значение функции на отрезке [а; b] называют максимумом функции на отрезке [а; b] В) Наименьшее значение функции на отрезке [а; b] называют минимумом функции на отрезке [а; b] Подберите правильный ответ
А - да, В - нет
А - нет, В - да
А - нет, В - нет
А - да, В - да
(u - v)' =________, где u = u(x), v = v(x)
u'-v'
2u + 2v
u'+v' - u'v'
u - v
Производная функции f(x) = cos x в точке с абсциссой x = 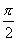равна ___
равна ___-1
0
1
0,5
Производная функции f(x) = sin x в точке с абсциссой x = 0 равна ___
1
0
-1
0,5
Производная функции f(x) = ax2 + bx + c в любой точке x равна ___
0,5x + b
2ax + b + с
2a+с
2ax + b
Если функции u(x) и v(x) имеют производные в точке x и v(x)≠0, то их частное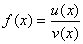 
также имеет в этой точке производную, равную: 
__________________
также имеет в этой точке производную, равную: __________________
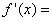Пусть функция y = f(x) непрерывна на интервале (а; b) и имеет в точке х0 Î (а; b) производную. Тогда график этой функции имеет в точке (х0; f(x0)) касательную, уравнение которой ___________, где y0 = f(x0), k=f '(x0)
y - у0= k (x - х0)
y - у0= kх0
y - у0= kx
y - у0= k (x + х0)
Предел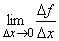 
(если он существует) в точке x, когда рассматривается только Dх>0, называют ___________ производной функции f в точке x
(если он существует) в точке x, когда рассматривается только Dх>0, называют ___________ производной функции f в точке xправой
верхней
левой
нижней
Верны ли утверждения? А) Минимум функции f(x) на интервале (0; 6) достигается в точке x = 2 В) Максимум функции f(x) на интервале (0; 6) равен 4 Подберите правильный ответ
А - нет, В - да
А - да, В - да
А - да, В - нет
А - нет, В - нет
Вторую производную функции f(x) обозначают так: _______
f '(2x)
f2 ‘(x)
f "(x)
2f ‘(x)
Пусть функция y = f(x) имеет производную в точке х0 и требуется найти приближенно значение этой функции в достаточно близкой к точке х0 точке x = х0+ Dх. Тогда применяется приближенное равенство: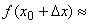 
________________
________________
Верны ли утверждения? А) Для любого действительного x≠pk, kÎZ справедлива формула: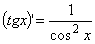 
В) Для любого действительного 
, 
, справедлива формула: 
Подберите правильный ответ
В) Для любого действительного 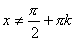, , 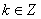справедлива формула: 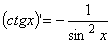Подберите правильный ответА - нет, В - да
А - да, В - да
А - нет, В - нет
А - да, В - нет
______.
Пусть а > 0 и а ≠ 1, тогда для любого x > 0 справедлива формула: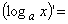 
__________
__________
Верны ли утверждения? А) Если функция y = f(x) непрерывна на отрезке [а; b], то существует точка этого отрезка, в которой функция принимает свое наибольшее значение В) Если функция y = f(x) непрерывна на отрезке [а; b], то существует точка этого отрезка, в которой функция принимает свое наименьшее значение Подберите правильный ответ
А - нет, В - да
А - да, В - нет
А - нет, В - нет
А - да, В - да
Пусть на промежутке I с концами а и b функция f(x) непрерывна вместе со своими первой и второй производными и х0 - единственная ее критическая точка на интервале (а; b). Тогда если f'(x0) = 0 и f"(x0) < 0, то точка х0 есть точка __________ на промежутке I
Пусть функция y = f(x) непрерывна на интервале (М; +∞), где М - некоторое число. Если при x®+∞ расстояние (в направлении оси Оу) от точки А(x; f(x)) кривой Г до точки В(x; kx + b) прямой L стремится к нулю, то прямую L называют _________ кривой Г (при x®+∞)
Пусть функция y = f(x) непрерывна на промежутке I и имеет производную f ’(x) в каждой точке внутри промежутка I. Тогда если f '(x) ________ внутри промежутка I, то функция f убывает на промежутке I
<0
>0
=0
£1
Верны ли утверждения? А) При отыскании максимума функции на отрезке надо найти критические точки, лежащие внутри этого отрезка, и сравнить значения функции на концах отрезка и в критических точках В) При отыскании минимума функции на отрезке надо найти критические точки, лежащие внутри этого отрезка, и сравнить значения функции на концах отрезка и в критических точках Подберите правильный ответ
А - да, В - нет
А - нет, В - нет
А - да, В - да
А - нет, В - да
Минимум функции f(x) = |x - 2| на отрезке [0; 6] равен ________
1
0
-2
4
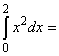