Алгебра и начала анализа (11 класс)
Если функция y = f(x) имеет производную в точке х0, являющейся точкой ее локального экстремума, то производная в этой точке равна _____
+¥
-1
1
0
Если каждая из функций u1(x), u2(x), ... , un(x) имеет в точке x производную и А1, А2, ... , Аn - данные числа, то справедливо равенство: (A1u1 + A2u2 +…+ Anun)' = ______________
A1'u1' + A2'u2' +…+ An'un'
A1'u1 + A2'u2 +…+ An'un
A1u1' + A2u2' +…+ Anun'
A1 + A2 +…+ An
Точку отрезка [а; b], в которой функция достигает максимума на этом отрезке, называют ______________
наибольшим значением аргумента
максимумом функции
максимумом аргумента
точкой максимума
Для любого xÎR и любого натурального n³2 справедлива формула: (хn)' = ____________
x'×n'
(n-1)×хn
nхn-1
Если при Dх ®0 отношение 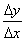 стремится к конечному пределу, то график функции y(x) имеет в точке А касательную, тангенс угла наклона которой с положительным направлением оси Ох равен этому пределу, а именно _____________
стремится к конечному пределу, то график функции y(x) имеет в точке А касательную, тангенс угла наклона которой с положительным направлением оси Ох равен этому пределу, а именно _____________
Если функции u(x) и v(x) имеют производные в точке x, то их произведение f(x) = u(x) × v(x) также имеет в этой точке производную, равную f ’(x) = _________________
u'(x) + v'(x)
u'(x) - v'(x)
u'(x) × v(x) + u(x) × v'(x)
u'(x)v'(x)
Верны ли утверждения? А) Для любого xÎR и любого натурального n³2 справедлива формула: (хn)' = nхn-1 В) Для любого xÎR, кроме x = 0, и любого натурального n справедлива формула: (х-n)' = -nх-n-1 Подберите правильный ответ
А - нет, В - да
А - нет, В - нет
А - да, В - нет
А - да, В - да
Верны ли утверждения? А) Точкой локального максимума функции f(х) называют точку х0 отрезка [а; b], для которой существует отрезок [х0 - d; х0 + d] (d>0), целиком принадлежащий отрезку [а; b], на котором х0 является точкой максимума В) Точкой локального минимума функции f(x) называют точку х0 отрезка [а; b] , для которой существует отрезок [х0 - d; х0 + d] (d>0), целиком принадлежащий отрезку [а; b], на котором х0 является точкой минимума Подберите правильный ответ
А - да, В - нет
А - да, В - да
А - нет, В - да
А - нет, В - нет
Если функции u(x) и v(x) имеют в точке x производные, то их сумма f(x) = u(x) + v(x) также имеет в этой точке производную, равную f ’(x) = _____________
u'(x) + v'(x)
u'(x) + v'(x) - u'(x)v'(x)
u'(x)v'(x)
u'(x) + v'(x) - 2u'(x)v'(x)
Уравнение касательной к графику функции f(x) = -х2+ 6х - 7, параллельной прямой y = 4х + 5 имеет вид y + 2=4(x - 1), т.е. y = ___________
6х - 7
4х
4х + 2
4х - 6
Для любого xÎR справедлива формула: (cosx)' = ____________
-sinx
-cosx
x sinx
-x sinx
Верны ли утверждения? А) Точки локального экстремума принадлежат интервалу (а; b) или совпадают с границами а и b отрезка [a; b] В) Если функция y = f(x) имеет производную в точке х0, являющейся точкой ее локального экстремума, то производная в этой точке равна нулю Подберите правильный ответ
А - да, В - нет
А - нет, В - да
А - да, В - да
А - нет, В - нет
Точку отрезка [а; b], в которой функция достигает минимума на этом отрезке, называют ______________
минимумом аргумента
наименьшим значением аргумента
минимумом функции
точкой минимума
______________ функция - функция y = f(x) с областью определения X, для которой для любого х Î Х число (-x) Î Х и справедливо равенство f(-x) = f(x)
_____________ скоростью движущейся точки в момент времени t называют предел (если он существует) отношения приращения пути к приращению времени, когда последнее стремится к нулю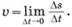
В механике ___________ движением называют движение, ускорение которого постоянно
Верны ли утверждения? А) Если функции u(x) и v(x) имеют производные в точке x, то их произведение f(x) = u(x) × v(x) также имеет в этой точке производную, равную f ’(x)=u'(x)×v(x)-u(x)×v'(x) В) Если функции u(x) и v(x) имеют производные в точке x и v(x)≠0, то их частное 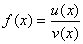 также имеет в этой точке производную, равную:
также имеет в этой точке производную, равную: 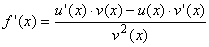 Подберите правильный ответ
Подберите правильный ответ
А - да, В - нет
А - нет, В - нет
А - да, В - да
А - нет, В - да
Производная функции f(x) = C, где С = const в любой точке x равна ____
0
1
C
x
Приращение функции y = f(x) в точке x равно: ___________________
Dx
f(x+Dx) - f(x)
f(x)
Внутреннюю точку х0 промежутка I, т.е. точку, принадлежащую интервалу (а; b), называют критической точкой функции f(x), если производная f ’(x) в этой точке ___________ (два варианта)
равна 1
равна нулю
равна -1
не существует
Производная функции f(x) = 0,2x5 + 2x3 + c в любой точке x равна ___
0,2x4 + 2x2
х4 + 6x2
0,2x4
5,2х4 + 12x + с
Уравнение касательной к графику функции f(x) = x2, проходящей через точку графика с абсциссой х0 = -2 имеет вид: y = _____________
2х - 2
-4х2 - 4
2х
-4х – 4
Верны ли утверждения? А) Постоянное число С, рассматриваемое как функция от x, имеет производную, равную нулю для всех x В) Если про функцию известно, что ее производная равна нулю для всех x, то она есть постоянная Подберите правильный ответ
А - нет, В - да
А - да, В - нет
А - да, В - да
А - нет, В - нет
Функция f(x) = х3 - 3х2 на отрезке [-1; 4] достигает максимума в точке x = _____
4
1
2
-1
Нечетная функция - функция y = f(x) с областью определения X, для которой для любого xÎ X число (-x) Î X и справедливо равенство
f(-x) = -f(x)
f(-x) = -(2n+1)f(x), nÎZ
f(-x) = -3f(x)
f(-x) = f(x)
______________ трапецией называется фигура, ограниченная кривой - графиком функции y = f(x), осью Ох, прямыми x = а, x = b
___________________ интегралом от непрерывной на интервале (а; b) функции f(x) называют любую ее первообразную функцию
Верны ли утверждения? А) 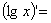
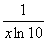 В)
В) 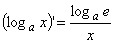 Подберите правильный ответ
Подберите правильный ответ
А - да, В - нет
А - нет, В - нет
А - да, В - да
А - нет, В - да
Угол ____________ касательной - угол между этой касательной и положительным направлением оси Ох
наклона
поворота
схождения
параллелизма
Точкой __________ максимума функции f(х) называют точку х0 отрезка [а; b], для которой существует отрезок [х0 - d; х0 + d] (d>0), целиком принадлежащий отрезку [а; b], на котором х0 является точкой максимума
Для любого xÎR справедлива формула: (sinx)' = ____________
cosx
-cosx
x sinx
-x sinx
Верны ли утверждения? А) Для любого действительного 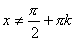 ,
, 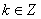 справедлива формула:
справедлива формула: 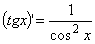 В) Для любого действительного x≠pk, kÎZ, справедлива формула:
В) Для любого действительного x≠pk, kÎZ, справедлива формула: 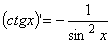 Подберите правильный ответ
Подберите правильный ответ
А - да, В - да
А - да, В - нет
А - нет, В - нет
А - нет, В - да
Производная функции f(x) = tg x в точке с абсциссой x = 0 ___________
= 1
= 0
не существует
=-1
Предел 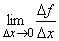 (если он существует) в точке x, когда рассматривается только Dх>0, называют ___________ производной функции f в точке x
(если он существует) в точке x, когда рассматривается только Dх>0, называют ___________ производной функции f в точке x
Производная функции f(x) = kx + b, где k и b - данные числа, в любой точке x равна ___
0
1
b
k
Производная функции f(x) = 2x3 + c в любой точке x равна ___
6х2+с
5x2
12x
6х2
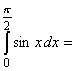 ______
______