Алгебра и начала анализа (11 класс)
для любого x > 0 равна __________
Производная функции f(x) = x5 + x3 + 4 в точке с абсциссой x = 0 равна ___
12
4
0
1
___________________ интегралом от непрерывной на интервале (а; b) функции f(x) называют любую ее первообразную функцию
Неопределенным
Первообразным
Определенным
Криволинейным
Вторая производная функции: f(x) = cos x равна f "(x) = ____________
-cos x
cos x
sin x
-sin x
Пусть на промежутке I с концами а и b функция f(x) непрерывна вместе со своей производной f ’(x) и х0 - единственная ее критическая точка на интервале (а; b). Тогда если на интервале (а; b) найдутся точки х1 и х2, такие, что х1< х0< х2 и f'(x1)< 0, f'(x2)> 0, то в точке х0 функция f достигает своего _______________ на промежутке I
Производная функции f(x) = -cos x в точке с абсциссой x = 0 равна ___
0
0,5
-1
1
(sin(kx + b))’ = _____________
ksin (2×(kx + b))
0,5×ksin (2×(kx + b))
ksin(kx + b)
kcos(kx + b)
______Верны ли утверждения? А) Если функция f(x) непрерывна на промежутке I и имеет внутри промежутка производную f ’(x) и если f '(x) > 0 внутри промежутка I, то функция f возрастает на промежутке I В) Если функция f(x) непрерывна на промежутке I и имеет внутри промежутка производную f ’(x) и если f ’(x) < 0 внутри промежутка I, то функция f убывает на промежутке I Подберите правильный ответ
А - да, В - нет
А - да, В - да
А - нет, В - да
А - нет, В - нет
Наибольшее значение функции на отрезке [а; b] называют ___________ функции на отрезке [а; b]
Тангенс угла наклона касательной к графику функции f(x) = 2х2 - 2х + 10 в точке с абсциссой x = 2 равен ______
8
14
6
4
______Четвертая производная функции: f(x) = sin x равна f (4)(x) = ____________
sin x
cos x
-sin x
-cos x
Функция f(x) = х3 - 3х2 на отрезке [-1; 4] достигает минимума (y = ______) в двух точках: x = -1 и x = 2
4
-4
-1
0
Широко употребляются следующие обозначения производной: ____________
x(y)
y’
y’x
df(x’)
Точки, в которых производная функции равна нулю или не существует, называют ________________ точками этой функции
Точкой _______________ минимума функции f(x) называют точку х0 отрезка [а; b] , для которой существует отрезок [х0 - d; х0 + d] (d>0), целиком принадлежащий отрезку [а; b], на котором х0 является точкой минимума
отрезочного
точечного
локального
глобального
Максимум функции f(x) = |x - 2| на отрезке [0; 6] равен ________
4
0
2
6
Верны ли утверждения? А) Если функция F(x) есть некоторая первообразная для функции f(x) на интервале (а; b), то неопределенный интеграл от функции f на этом интервале равен 
, где С - любая постоянная В) Если f1(x) и f2(x) - непрерывные на интервале (а; b) функции и А1 и А2 - постоянные, то имеет место равенство, выражающее основное свойство неопределенного интеграла: 
, где С - любая постоянная Подберите правильный ответ
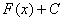, где С - любая постоянная В) Если f1(x) и f2(x) - непрерывные на интервале (а; b) функции и А1 и А2 - постоянные, то имеет место равенство, выражающее основное свойство неопределенного интеграла: 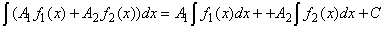, где С - любая постоянная Подберите правильный ответА- да, В- нет
А- нет, В- да
А- нет, В- нет
А- да, В- да
Приращение функции f(x) = 3х + 2 в любой точке x, соответствующее приращению Dх аргумента, равно ___________
3Dх+2
3Dх
Dх
5
Вторая производная функции: f(x) = х4 + х3 + х2 + x + 1 равна f "(x) = ____________
4х3 + 3х2 + 2х+1
х2 + x + 1
12х2 + 6х + 2
4х2 + 3х + 1
Пусть на промежутке I с концами а и b функция f(x) непрерывна, а ее производная f ’(x) существует, непрерывна и отлична от нуля во всех точках интервала, кроме точки х0, в которой производная не существует. Тогда если на интервале (а; b) найдутся точки х1 и х2, такие, что х102 и f'(x1)<0, f'(x2)>0, то в точке х0 функция f достигает своего ________________ на промежутке I
Равенство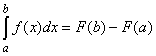 
называют формулой _____________
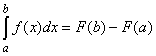называют формулой _____________Эйлера
Ньютона - Лейбница
Ньютона - Эйлера
Декарта
(u + v)'=________, где u = u(x), v = v(x)
u'+v' - 2 u'v'
u'v + v'u
u'+v'
2u + 2v
_____________ являются основателями дифференциального и интегрального исчислений
Ньютон
Лейбниц
Декарт
Фурье
_________
Постоянное число С, рассматриваемое как функция от x, имеет производную, равную ____________ для всех x
+∞
1
-С
0
Производная функции sin3x2 равна __________
2x sin3x2 cos x2
3x sin2x2 cos x2
6x sin2x2 cos x2
sin2x2
Производную функции f(x) обозначают ____________
f(x’)
ff(x)
x(f)
f ’(x)
Верны ли утверждения? А) Если f(x)³0 на отрезке [а; b], то определенный интеграл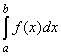 
равен площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b В) Если f(x)£0 на отрезке [а; b], то определенный интеграл 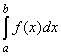равен взятой со знаком «минус» площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b Подберите правильный ответ
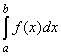равен площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b В) Если f(x)£0 на отрезке [а; b], то определенный интеграл 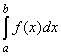равен взятой со знаком «минус» площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b Подберите правильный ответА - да, В - да
А - нет, В - да
А - да, В - нет
А - нет, В - нет
Производная функции f(x) = -sin x в точке с абсциссой x =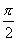 
равна ___
равна ___-1
0
1
2
Пусть на промежутке I с концами а и b функция f(x) непрерывна вместе со своей производной f ’(x) и х0 — единственная ее критическая точка на интервале (а; b). Тогда если на интервале (а; b) найдутся точки х1 и х2, такие, что х1< х0< х2 и f'(x1)> 0, f'(х2) <0, то в точке х0 функция f достигает своего ____________ на промежутке I
___________ функции y = f(x) - множество тех и только тех точек координатной плоскости хОу, координаты x и y которых удовлетворяют условию y = f(x)
График
Отрезок
Промежуток
Интервал
Если функции u(x) и v(x) имеют в точке x производные, то их разность f(x) = u(x) - v(x) также имеет в этой точке производную, равную f '(x) = ________________
u'(x) + v' (x)
u'(x) - v' (x)
u'(x)v(x)- v'(x)u(x)
u'(x)×v' (x) - u(x)×v(x)
Верны ли утверждения? А) Значение функции в точке максимума на отрезке [a; b] и есть максимум функции на этом отрезке В) Значение функции в точке минимума на отрезке [a; b] и есть минимум функции на этом отрезке Подберите правильный ответ
А - да, В - да
А - да, В - нет
А - нет, В - да
А - нет, В - нет
Верны ли утверждения? А) Минимум функции на интервале или полуинтервале может не достигаться В) Максимум функции на интервале или полуинтервале может не достигаться Подберите правильный ответ
А - да, В - да
А - нет, В - да
А - да, В - нет
А - нет, В - нет
Верны ли утверждения? А) Максимум функции f(x) = |x - 2| на отрезке [0; 6] равен 4 В) Минимум функции f(x) = |x - 2| на отрезке [0; 6] не существует Подберите правильный ответ
А - нет, В - нет
А - да, В - нет
А - да, В - да
А - нет, В - да
Если производная на всем интервале сохраняет один и тот же знак, то функция f возрастает на промежутке I, если f ’(x)>0, или убывает на промежутке I, если f ’(x)<0, т.е. функция f ________ монотонна на промежутке I
_____________ (а; b) - множество всех действительных чисел x, удовлетворяющих двойному неравенству: а<>
Интервал
Вектор
Полуинтервал
Отрезок
_____________ функция - функция y = f(x) с областью определения X, для которой для любого xÎ X число (-x) Î X и справедливо равенство f(-x) = -f(x)
Наименьшее значение функции на отрезке [а; b] называют ___________ функции на отрезке [а; b]
Верны ли утверждения? А) Максимум функции на отрезке [а; b] и обозначают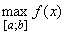 
В) Минимум функции на отрезке [а; b] и обозначают 
Подберите правильный ответ
В) Минимум функции на отрезке [а; b] и обозначают 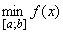Подберите правильный ответА - да, В - нет
А - нет, В - нет
А - нет, В - да
А - да, В - да
=________
Тангенс угла наклона касательной к графику функции f(x) = 3х2 - 5х + 7 в точке с абсциссой x = 1 равен ______
1
-2
5
8
Верны ли утверждения? А) Точку отрезка [а; b], в которой функция достигает максимума на этом отрезке, называют точкой максимума В) Точку отрезка [а; b], в которой функция достигает минимума на этом отрезке, называют минимумом функции Подберите правильный ответ
А - да, В - нет
А - нет, В - нет
А - нет, В - да
А - да, В - да
____________ функции - функции возрастающие, убывающие, невозрастающие и неубывающие
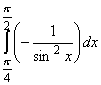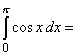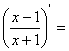