Алгебра и начала анализа (11 класс)
Производная функции f(x) = x3 + 4 в точке с абсциссой x = 2 равна ___
8
24
4
12
__________________ функции y = f(x), заданной на некотором интервале (а; b), в точке x этого интервала называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю
Областью определения функции
Производной
Первообразной
Аргументом
Расположите по порядку действия необходимые для вычисления максимума и минимума функции f(x) на отрезке [a; b]
нахождение производной f ’(x)
нахождение наибольшего и наименьшего из чисел f(a), f(b), f(x1), f(x2) …f(xn)
вычисление значения функции в точках, где f ’(x) = 0: x1, x2 … xn.
приравнивание решение уравнения f ’(x) = 0
Четвертая производная функции: f(x) = cos x равна f (4)(x) = ____________
sin x
-sin x
cos x
-cos x
Производная функции f(x) при данном x из интервала (а; b) (если она в этой точке x существует) есть __________
функция
промежуток
число
интервал
Основные свойства определенного интеграла выражаются формулами
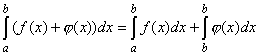
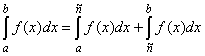
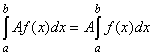, где А - данная постоянная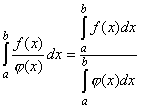
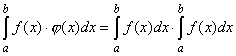
Число Dх называют _______________
приращением функции
приращением зависимой переменной
приращением аргумента
производной
, 
справедлива формула: 
________
Если вычислить приближенно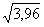 
, то получится » ___________
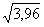, то получится » ___________1,99
1,29
0,49
1,09
Если при прямолинейном движении путь s, пройденный точкой, есть функция от времени t, т.е. s = f(t), то скорость точки есть производная от пути по времени, т.е. v(t) = f ’(t). Этот факт выражает ______________ смысл производной
механический
математический
геометрический
алгебраический
______________ функции - функции, которые задаются формулой: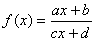 
, где а, b, с, d - данные числа, причем с≠0 и ad – bс ≠ 0
, где а, b, с, d - данные числа, причем с≠0 и ad – bс ≠ 0Дробно-линейные
Иррациональные
Линейные
Дробные
Если точка движется по закону s = f(t), то механический смысл второй производной заключается в том, что вторая производная определяет ______________ этой точки
ускорение
скорость
время движения
путь
Две прямые ____________ являются асимптотами графика функции y =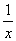
y = -1
x = 1
x = 0
y = 0
Точку отрезка [а; b], в которой функция достигает максимума на этом отрезке, называют точкой ______________
Приращение функции y = f(x) в точке x обозначают: _______________ (два обозначения)
Df
Dу
Dx
Если функция u(x) имеет в точке x производную и А - данное число, то функция f(x) = A × u(x) также имеет в этой точке производную, равную f ’(x) = A × u'(x)
A
u(x)
A × u(x)
A × u'(x)
________________ асимптота – асимптота, в уравнении y = kx + b которой k = 0
Верны ли утверждения? А) Минимум функции f(x) на интервале (0; 6) достигается в точке x = 6 В) Максимум функции f(x) на интервале (0; 6) не существует Подберите правильный ответ
А - нет, В - да
А - да, В - нет
А - нет, В - нет
А - да, В - да
Геометрический смысл определенного интеграла заключается в том, что: ______________
если f(x)£0 на отрезке [а; b], то определенный интеграл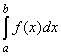 
равен взятой со знаком «минус» площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b
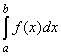равен взятой со знаком «минус» площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = bесли f(x)£0 на отрезке [а; b], то определенный интеграл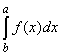 
равен взятой со знаком «минус» площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b
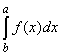равен взятой со знаком «минус» площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = bесли f(x)³0 на отрезке [а; b], то определенный интеграл 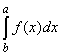равен площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b
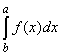равен площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = bесли f(x)³0 на отрезке [а; b], то определенный интеграл 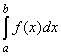равен площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b
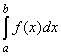равен площади криволинейной трапеции, ограниченной линиями y = f(x), y = 0, x = а, x = b
для любого x > 0 равна __________
Функция f(x) = х3 является возрастающей ______________
только на интервале [0; + 1]
на всем интервале (-∞; + ∞)
только на полуинтервале [-∞; 0)
только на полуинтервале [0; + ∞)
Установите соответствие
(arccos x)’
-
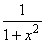
(arctg x)’
(arcsin x)’
(arcctg x)’
______Верны ли утверждения? А) Если функции u(x) и v(x) имеют в точке x производные, то их сумма f(x) = u(x) + v(x) также имеет в этой точке производную, равную f ’(x) = u'(x) + v'(x) В) Если функция u(x) имеет в точке x производную и А - данное число, то функция f(x) = A × u(x) также имеет в этой точке производную, равную f ’(x) = A × u'(x) Подберите правильный ответ
А - нет, В - нет
А - нет, В - да
А - да, В - да
А - да, В - нет
Минимум функции f(x) = |x – 2| на интервале (0; 6) достигается в точке x = _______
0
2
6
4
Верны ли утверждения? А) При Dх, близких к нулю, справедливо приближенное равенство: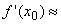 
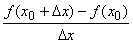, которое выполняется тем точнее, чем ближе значение Dх к нулю В) Если функция f(x) непрерывна на промежутке I и имеет внутри промежутка производную f ’(x), то по знаку производной можно заключить, возрастает или убывает она на промежутке I Подберите правильный ответ
, которое выполняется тем точнее, чем ближе значение Dх к нулю В) Если функция f(x) непрерывна на промежутке I и имеет внутри промежутка производную f ’(x), то по знаку производной можно заключить, возрастает или убывает она на промежутке I Подберите правильный ответА - да, В - нет
А - нет, В - нет
А - да, В - да
А - нет, В - да
Точкой _______________ минимума функции f(x) называют точку х0 отрезка [а; b] , для которой существует отрезок [х0 - d; х0 + d] (d>0), целиком принадлежащий отрезку [а; b], на котором х0 является точкой минимума
Если в точке х0 к графику функции y = f(x) проведена касательная, то число f '(x0) есть тангенс угла α между этой касательной и ________________
отрицательным направлением оси Оy
отрицательным направлением оси Ох
положительным направлением оси Ох
положительным направлением оси Оy
Верны ли утверждения? А) Точки локального экстремума есть внутренние точки отрезка [а; b], т.е. они принадлежат интервалу (а; b) В) Если функция y = f(x) имеет производную в точке х0, являющейся точкой ее локального экстремума, то производная в этой точке равна единице Подберите правильный ответ
А - нет, В - да
А - да, В - нет
А - нет, В - нет
А - да, В - да
При Dх, близких к нулю, справедливо приближенное равенство: 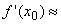__________, которое выполняется тем точнее, чем ближе значение Dх к нулю
__________, которое выполняется тем точнее, чем ближе значение Dх к нулю
Если в точке х0 к графику функции y = f(x) проведена касательная, то число f '(x0) есть ____________ угла α между этой касательной и положительным направлением оси Ох
синус
тангенс
котангенс
косинус
____________ интегралом от функции f на отрезке [а; b] называют предел интегральной суммы, когда длина максимального частичного отрезка разбиения стремится к нулю
_____________Если точка движется по прямой по квадратичному закону: s = at2 + bt + c, где a, b и с — данные числа и а ≠ 0, то это движение ______________, так как его скорость s' = 2at + b зависит от времени
Пусть на промежутке I с концами а и b функция f(x) непрерывна, а ее производная f ’(x) существует, непрерывна и отлична от нуля во всех точках интервала, кроме точки х0, в которой производная не существует. Тогда если на интервале (а; b) найдутся точки х1 и х2, такие, что х102 и f'(х1)>0, f'(x2)<0, то в точке х0 функция f достигает своего __________ на промежутке I
Если вычислить приближенно значение функции f(x) = х10 в точке x = 1,01, то получится f(1,01) » ___________
1,2
0,9
1,1
1,01
Если в точке х0 производная меняет знак с «-» на «+», то х0 — точка локального ________________
Мгновенная скорость движущейся точки в момент времени t равна ______________
Точки локального максимума и локального минимума функции y = f(x) называют точками ___________ этой функции
локального экстремума
локальной вершины
локального мини-максимума
локального макси-минимума
Прямые, к которым неограниченно приближаются точки графика функции при удалении в бесконечность называют ______________ графика функции
биссектрисами
медианами
высотами
асимптотами
Если точка движется по прямой по линейному закону: s = at + b, где а и b — данные числа и а ≠ 0, то это движение ________
Установите соответствие
точка отрезка [а; b], в которой функция достигает минимума на этом отрезке
минимум функции на отрезке [а; b]
наибольшее значение функции на отрезке [а; b]
точка максимума
точка отрезка [а; b], в которой функция достигает максимума на этом отрезке
максимум функции на отрезке [а; b]
наименьшее значение функции на отрезке [а; b]
точка минимума
Точкой __________ максимума функции f(х) называют точку х0 отрезка [а; b], для которой существует отрезок [х0 - d; х0 + d] (d>0), целиком принадлежащий отрезку [а; b], на котором х0 является точкой максимума
глобального
локального
отрезочного
точечного
______Для любого xÎR справедливы формулы: ____________
(sinx)' = cosx
(cosx)' = -sinx
(-sinx)' = cos(-x)
(-cosx)' = sin(-x)
Разность значений функции в точках x+Dх и x называют приращением ____________
Предел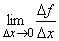 
(если он существует) в точке x, когда рассматривается только Dх<0, называют ___________ производной функции f в точке x
(если он существует) в точке x, когда рассматривается только Dх<0, называют ___________ производной функции f в точке xлевой
нижней
правой
верхней
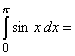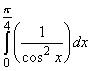