Алгебра и начала анализа (11 класс)
______В механике ___________ движением называют движение, скорость которого постоянна
Пусть функция y = f(x) непрерывна на промежутке I и имеет производную f ’(x) в каждой точке внутри промежутка I. Установите соответствие
если f ’(x) = 0 для всех x внутри промежутка I
функция y = f(x) убывает на промежутке I
если f ’(x)>0 для всех x внутри промежутка I
функция y = f(x) возрастает на промежутке I
если f ’(x)<0 для всех x внутри промежутка I
функция y = f(x) есть постоянная (константа) на промежутке I
Верны ли утверждения? А) Производная интеграла (как функции верхнего предела) равна подынтегральной функции взятой со знаком «-» В)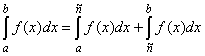 
Подберите правильный ответ
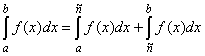Подберите правильный ответА - нет, В - нет
А - да, В - да
А - нет, В - да
А - да, В - нет
Минимум функции f(x) = |x – 2| на интервале (0; 6) _______
= 2
= 4
не существует
= 0
Верны ли утверждения? А) Про функцию f(x), заданную на отрезке [а; b], принято говорить, что она имеет производную на этом отрезке, если она имеет производную в любой точке интервала (а; b) и, кроме того, правую производную в точке а и левую - в точке b В) Предел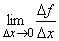 
(если он существует) в точке x, когда рассматривается только Dх>0, называют левой производной функции f в точке x Подберите правильный ответ
(если он существует) в точке x, когда рассматривается только Dх>0, называют левой производной функции f в точке x Подберите правильный ответА - да, В - да
А - нет, В - нет
А - да, В - нет
А - нет, В - да
___________ функции y = f(x) - множество тех и только тех точек координатной плоскости хОу, координаты x и y которых удовлетворяют условию y = f(x)
Если функция y = f(x) непрерывна на интервале (а; b) и ес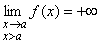ли 
или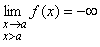 
, то говорят, что прямая x = а является ____________ асимптотой графика функции y = f(x)
или , то говорят, что прямая x = а является ____________ асимптотой графика функции y = f(x)Если при прямолинейном движении путь s, пройденный точкой, есть функция от времени t, т.е. s = f(t), то скорость точки есть производная от пути по времени, т.е. v(t) = ________
2f’(t)
t’(s)
t’
f’(t)
Третья производная функции: f(x) = cos x равна f ‘’’(x) = ____________
cos x
sin x
-cos x
-sin x
Пусть а > 0 и а ≠ 1, тогда для любого xÎR справедлива формула: (ах)' = __________
ах ln а
xах lg а
(x-1)ах
xах-1
________________ асимптота – асимптота, в уравнении y = kx + b которой k ≠ 0
Верны ли утверждения? А) Пусть а > 0 и а ≠ 1, тогда для любого x > 0 справедлива формула: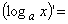 
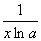В) 
Подберите правильный ответ
В) 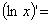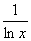Подберите правильный ответА - нет, В - да
А - нет, В - нет
А - да, В - нет
А - да, В - да
Для любого xÎR, кроме x = 0, и любого натурального n справедлива формула: (х-n)' = ___
-nх-n-1
nх-n-1
х-n-1
-х-n-1
Результат выполнения дифференцирования функции называют _______________
Предел 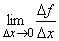(если он существует) в точке x, когда рассматривается только Dх<0, называют ___________ производной функции f в точке x
(если он существует) в точке x, когда рассматривается только Dх<0, называют ___________ производной функции f в точке xЕсли в точке х0 производная меняет знак с «+» на «-», то х0 — точка локального _______________
Если функция F(x) есть некоторая первообразная для функции f(x) на интервале (а; b), то неопределенный интеграл от функции f на этом интервале равен 
_____________
_____________
, где С - любая постоянная
Функция f(x) = х3 является ____________ на всем интервале (-∞; + ∞)
невозрастающей
возрастающей
неопределенной
убывающей
Пусть функция y = f(x) непрерывна на промежутке I и имеет производную f ’(x) в каждой точке внутри промежутка I. Тогда если f '(x) ________ внутри промежутка I, то функция f возрастает на промежутке I
>0
=0
<0
£1
Производная функции f(x) = сtg x в точке с абсциссой x =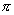 
_____________
_____________=-1
= 0
= 1
не существует
Производная функции f(x) = tg x в точке с абсциссой x =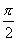 
___________
___________= 1
=-1
не существует
= 0
Функция f(x) = х3 - 3х2 на отрезке [-1; 4] достигает максимума (y =_____) в точке x = 4
-2
16
4
-16
Если производная функции f(x) существует при каждом значении x из интервала (а; b), то производная есть __________ от x, определенная на интервале (а; b)
Пусть функция f непрерывна на промежутке I, имеет производную внутри его и критическая точка х0 лежит внутри I. Верны ли в таком случае утверждения? А) Если в точке х0 производная меняет знак с «+» на «-», то х0 — точка локального максимума В) Если в точке х0 производная меняет знак с «-» на «+», то х0 — точка локального минимума Подберите правильный ответ
А - да, В - нет
А - нет, В - да
А - да, В - да
А - нет, В - нет
______ + CОперация нахождения предела отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю называется ________________ функции
Интегрированием
Исследованием
Разложением
Дифференцированием
Установите соответстви
(cos x)‘‘
cos x
(cos x)‘
sin x
(cos x)‘‘‘
-sin x
(cos x)(4)
-cos x
_______________ [а; b] - множество всех действительных чисел x, удовлетворяющих двойному неравенству а £ x £ b, или множество точек оси x, состоящее из точек а и b и всех точек, находящихся между ними
Вектор
Полуинтервал
Отрезок
Интервал
_______
______________ для функции f(x) на интервале (а; b) - функция F(x), производная которой на этом интервале равна f: F ’(x) = f(x)
Производная функции f(x) = -cos x в точке с абсциссой x = 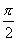равна ___
равна ___0
1
-1
0,5
Производная функции f(x) = сtg x в точке с абсциссой x = _____________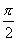
_____________=-1
не существует
= 0
= 1
Верны ли утверждения? А) Для любого xÎR справедлива формула: (sinx)' = cosx В) Для любого xÎR справедлива формула: (cosx)' = sinx Подберите правильный ответ
А - нет, В - да
А - нет, В - нет
А - да, В - нет
А - да, В - да
Производная функции f(x) = x2 в любой точке x равна ___
0,5x
2
2х
x
Точку отрезка [а; b], в которой функция достигает минимума на этом отрезке, называют точкой ______________
Если в точке х0 к графику функции y = f(x) проведена касательная, то число f '(x0) есть тангенс угла α между этой касательной и положительным направлением оси Ох, т.е. f '(x0) = tgα. Данный факт выражает __________________ смысл производной
механический
геометрический
вероятностный
алгебраический
Верны ли утверждения? А) Минимум функции f(x) на интервале (0; 6) равен 0 В) Максимум функции f(x) на интервале (0; 6) не существует Подберите правильный ответ
А - нет, В - нет
А - да, В - да
А - нет, В - да
А - да, В - нет
Приращение функции f(x) = х2 в любой точке x, соответствующее приращению Dх аргумента, равно ___________
Dх
(2x+Dх)Dх
Dх2
Dх+2
Верны ли утверждения? А) Функция f(x) = х3 - 3х2 на отрезке [-1; 4] достигает максимума в двух точках В) Функция f(x) = х3 - 3х2 на отрезке [-1; 4] достигает минимума в двух точках Подберите правильный ответ
А - да, В - да
А - нет, В - нет
А - да, В - нет
А - нет, В - да
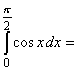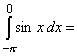