Основы математического анализа, часть II
Область определения функции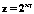 
есть множество
есть множество{(x, y) :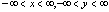 
}
}{(x, y) :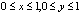 
}
}{(x, y) :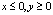 
}
}{(x, y) :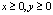 
}
}Корни дифференциального уравнения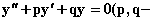 
постоянные) вещественные и различные 
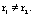Тогда общее решение этого уравнения имеет вид
постоянные) вещественные и различные Тогда общее решение этого уравнения имеет вид
функции 
равна
.
Частное решение разностного уравнения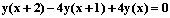 
, удовлетворяющее начальному условию 
, равно
, удовлетворяющее начальному условию 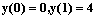, равно
Полный дифференциал функции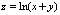 
равен
равенxdx - ydy
(dx - dy)(dx +dy)dx + dy
Общее решение дифференциального уравнения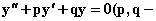 
постоянные) в случае равных корней характеристического уравнения 
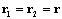имеет вид
постоянные) в случае равных корней характеристического уравнения имеет вид
ищется в виде
Полным дифференциалом функции z =f(x, y) называется выражение
f(x, y)dxdy
Полный дифференциал функции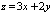 
в точке 
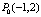равен
в точке равенdx + dy
3dx + 2dy
5(dx + dy)
2dx + 3dy
в точке 
функции 
равнаФормула для приближенного вычисления полного приращения функции z = f(x, y) в точке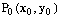 
имеет вид
имеет вид
Полный дифференциал функции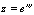 
равен
равенxdy + ydx
(dx dy)
(dx +dy)(ydx +xdy)
равно
Область определения функции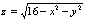 
есть множество
есть множествоO(0, 0)
{(x, y):-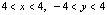
}
}{(x, y):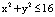 
}
}{(x, y):-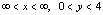
}
}Частное решение дифференциального уравнения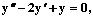 
удовлетворяющее начальным условиям y(0)=1, 
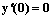равно
удовлетворяющее начальным условиям y(0)=1, равно
2x
Если в точке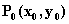 
функция f(x, y) имеет экстремум, то
функция f(x, y) имеет экстремум, точастные производные функции f(x, y) в точке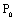 
не существуют
не существуютчастные производные функции f(x, y) в точке 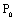равны нулю или не существуют
равны нулю или не существуютчастные производные функции f(x, y) в точке 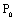равны бесконечности
равны бесконечностивторые частные производные по переменной x в точке 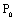равны нулю
равны нулюСтационарная точка для функции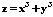 
имеет координаты
имеет координаты(-1, -1)
(1, 0)
(0, 1)
(0, 0)
Полный дифференциал функции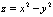 
в точке 
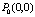равен
в точке равенdx - dy
2dx - 2dy
2dx + 2dy
0
Характеристическое уравнение для дифференциального уравнения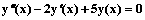 
имеет корни
имеет корни1, i
1-i, 1+i
2i, -2i
1+2i, 1-2i
функции 
в точке 
(1, 1, 1) равен
равно
Характеристическое уравнение для дифференциального уравнения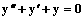 
имеет корни
имеет корни
имеет вид
равен
имеет вид
Полный дифференциал функции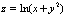 
равен
равен(x +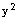 
)dx + dy
)dx + dy
(dx + dy)(dx + ydy)dx + 
dy
равен.
Область определения функции z = 2 ln xy есть множество
{(x, y) : x < 0, y < 0}
{(x, y) : x > 0, y > 0}
{(x, y) : xy > 1 }
{(x, y) : xy >0}
в точке 
Следующее условие достаточно для наличия максимума в стационарной точке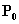 
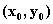для функции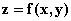 
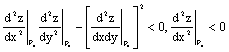
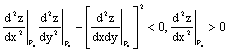
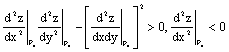
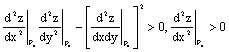
для функции 
Полный дифференциал функции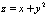 
в точке 
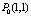равен
в точке равен2dx + 2dy
dx + 2dy
2dx + dy
dx + dy
равно
равно
Область определения функции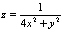 
есть множество
есть множествовся плоскость
O(0, 0)
{(x, y): x > 0, y>0}
вся плоскость X0Y, кроме точки O(0, 0)
Стационарная точка для функции 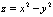имеет координаты
имеет координаты(1, 1)
(0, 1)
(-1,1)
(0, 0)
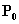
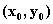Если точка является точкой экстремума дифференцируемой функции, то касательная плоскость к поверхноcти z = f(P) в точке 
является точкой экстремума дифференцируемой функции, то касательная плоскость к поверхноcти z = f(P) в точке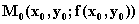 перпендикулярна плоскости Oxy
не существует
перпендикулярна плоскости xOz
параллельна плоскости Oxy
Линии уровня для функции z = ln(x2 - y2) имеют вид
ln(x2 - y2) = 1
x2 - y2 ³ 1
x2 - y2 = C, C > 0
x2 - y2 £ 1
Градиентом функции z = f(x, y) в точке 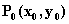называется
называетсявектор, равный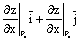 
число, равное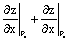 
число, равное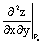 
вектор, равный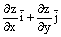 
Полный дифференциал функции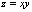 
в точке 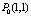равен
в точке равен2dx + 2dy
(x + y)dx + 2dy
dxdy
dx + dy
Линией уровня функции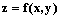 
называется совокупность всех точек плоскости, удовлетворяющих уравнению
называется совокупность всех точек плоскости, удовлетворяющих уравнениюf(x, y) = сonst
df(x, y) = 1
f(x, y) = 0
Полный дифференциал функции 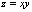равен
равен(x + y)dx + (y + x)dy
xydx dy
ydx +xdy
xdx + ydy
равно
Характеристическое уравнение для дифференциального уравнения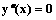 
имеет вид
имеет вид2r=0
r = 0
Поверхностью уровня для функции u = f(x, y, z) называется поверхность, определяемая уравнением
(x, y, z) = 0
= Cf(x, y, z) +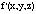 
= 1
= 1f(x, y, z) = C
