Линейная алгебра (курс 3)
Гиперболоид 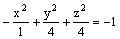 является
является
поверхностью вращения вокруг оси Ox
поверхностью вращения вокруг оси Oy
поверхностью вращения вокруг оси Oz
линейчатой поверхностью
Уравнением (x + 1)(x - 1) = 0 задается вырожденная поверхность второго порядка, представляющая собой
точку
пустое множество
две параллельные плоскости
прямую
Данная поверхность 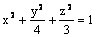 является
является
эллиптическим цилиндром
однополостным гиперболоидом
эллипсоидом
эллиптическим параболоидом
Уравнением x(x - z) = 0 задается вырожденная поверхность второго порядка, представляющая собой
две параллельные прямые
прямую
две пересекающиеся плоскости
пустое множество
Через точки М1(3,0,3), М2(-1,0,0) и М3(2,2,0) проходит плоскость
х-у-2z+5=0
х-2у-2z+2=0
х-2у-z+1=0
6х-9у-8z+6=0
Данная поверхность 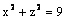 является
является
эллипсоидом
круговым цилиндром
гиперболическим цилиндром
конусом
Вектор 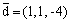 является
является
направляющим вектором прямой 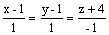
направляющим вектором прямой 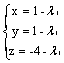
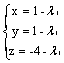
нормальным вектором плоскости (x - 1) + (y - 1) - 4z = 0
нормальным вектором плоскости x + y - 4 = 0
Уравнением x2 + y2 + z2 = -1 задается вырожденная поверхность второго порядка, представляющая собой
точку
плоскость
пустое множество
прямую
Уравнением x2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
точку
пустое множество
координатную плоскость Oyz
координатную плоскость Oxz
Данная поверхность 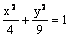 является
является
конусом
эллипсоидом
гиперболическим цилиндром
эллиптическим цилиндром
В пространстве Oxyz уравнение F(x, y, z) = 0 является уравнением данной поверхности, если
координаты (x, y, z) любой точки этой поверхности удовлетворяют этому уравнению
x2 + y2 + z2 ¹ 0
координаты (x, y, z) каждой точки этой поверхности удовлетворяют этому уравнению, а координаты любой точки, не лежащей на поверхности, этому уравнению не удовлетворяют
координаты любой точки (x, y, z) этой поверхности данному уравнению не удовлетворяют
Вектор 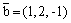
параллелен плоскости x + z + 5 = 0
перпендикулярен плоскости x - 1 + 2(y - 2) + (z + 1) = 0
перпендикулярен прямой 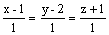
параллелен прямой 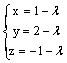
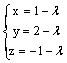
Данная поверхность 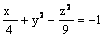 является
является
эллипсоидом
однополостным гиперболоидом
гиперболическим цилиндром
двухполостным гиперболоидом
Данная поверхность 2z = 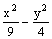 является
является
конусом
эллиптическим параболоидом
гиперболическим цилиндром
гиперболическим параболоидом
Уравнением первой степени относительно x, y называется уравнение вида
Ax + By + C = 0
F(x, y) = 0
Ax + By + C = 0, C ¹ 0
Ax + By + C = 0, A2 + B2 ¹ 0
Данная поверхность 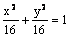 является
является
гиперболическим цилиндром
конусом
эллипсоидом
круговым цилиндром
Линейчатой поверхностью является
однополостный гиперболоид
эллипсоид вращения
эллиптический параболоид
двухполостный гиперболоид
Через точки М1(1,1,0), М2(1,0,1) и М3(-1,0,0) проходит плоскость
х-2у-2z+3=0
х-2у-z+1=0
х-у-2z+1=0
х-2у-2z+1=0
Верны ли утверждения? А) Каноническое уравнение оси OY имеет вид 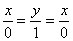 . В) Параметрическое уравнение оси OY имеет вид y = 0. Подберите правильный ответ
. В) Параметрическое уравнение оси OY имеет вид y = 0. Подберите правильный ответ
А – да, В – да
А – нет, В – да
А – нет, В – нет
А – да, В – нет
Через точку (1, 2, 4) проходит
прямая 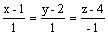
плоскость 4(x - 2) + 5(z - 1) = 0
прямая 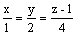
плоскость 2x + z = 0
Верны ли утверждения? А) Плоскость x + y + x – 6 = 0 параллельна плоскости XOY. В) Плоскость x + y +z – 6 = 0 перспекндикулярна оси OX. Подберите правильный ответ
А – да, В – нет
А – нет, В – нет
А – нет, В – да
А – да, В – да
Данная поверхность 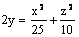 является
является
эллиптическим цилиндром
конусом
гиперболическим параболоидом
эллиптическим параболоидом
Данная поверхность 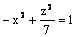 является
является
двухполостным гиперболоидом
однополостным гиперболоидом
гиперболическим цилиндром
эллиптическим цилиндром
Данная поверхность 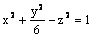 является
является
эллипсоидом
однополостным гиперболоидом
двухполостным гиперболоидом
гиперболическим цилиндром
Параболоид 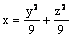 является
является
поверхностью вращения вокруг оси Oy
поверхностью вращения вокруг оси Oz
поверхностью вращения вокруг оси Ox
линейчатой поверхностью
Данная поверхность 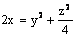 является
является
гиперболическим цилиндром
эллиптическим параболоидом
гиперболическим параболоидом
эллиптическим цилиндром
Через точку (1, 1, 2) проходит
прямая 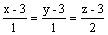
плоскость y + z + 2 = 0
плоскость x + y + 2z = 0
прямая 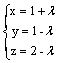
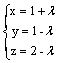
Верны ли утверждения? А) Ненулевой вектор 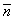 , перпендикулярный к плоскости a, называется вектором нормали этой плоскости. В) Две плоскости параллельны, если их векторы нормали коллинеарны. Подберите правильный ответ
, перпендикулярный к плоскости a, называется вектором нормали этой плоскости. В) Две плоскости параллельны, если их векторы нормали коллинеарны. Подберите правильный ответ
А – нет, В – да
А – да, В – да
А – да, В – нет
А – нет, В – нет
Данная поверхность 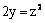 является
является
гиперболическим цилиндром
эллиптическим параболоидом
гиперболическим параболоидом
параболическим цилиндром
Параболоид 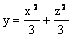 является
является
линейчатой поверхностью
поверхностью вращения вокруг оси Ox
поверхностью вращения вокруг оси Oy
поверхностью вращения вокруг оси Oz
Данная поверхность 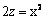 является
является
эллиптическим параболоидом
гиперболическим цилиндром
гиперболическим параболоидом
параболическим цилиндром
Прямая 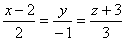 пересекает плоскость YOZ в точке
пересекает плоскость YOZ в точке
M(2, –1, 3)
M(2, 0, –3)
M(0, 1, –6)
M(–2, 0, 3)
Уравнением x2 + z2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
точку
пустое множество
прямую – ось ОУ
плоскость
Данная поверхность 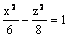 является
является
двухполостным гиперболоидом
однополостным гиперболоидом
гиперболическим цилиндром
эллиптическим цилиндром
Данная поверхность 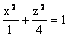 является
является
конусом
эллипсоидом
эллиптическим цилиндром
гиперболическим цилиндром
Параболоид 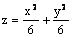 является
является
поверхностью вращения вокруг оси Ox
линейчатой поверхностью
поверхностью вращения вокруг оси Oz
поверхностью вращения вокруг оси Oy
Данная поверхность 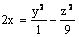 является
является
конусом
гиперболическим цилиндром
эллиптическим параболоидом
гиперболическим параболоидом
Данная поверхность 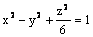 является
является
эллипсоидом
гиперболическим цилиндром
однополостным гиперболоидом
двухполостным гиперболоидом
Через точку (-3, 1, 5) проходит
прямая 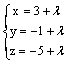
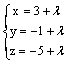
прямая 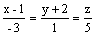
плоскость -3x + y + 5z + 1 = 0
плоскость x + 3y + z - 5 = 0
Через точку (0, 2, 1) проходит
прямая 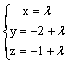
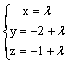
прямая 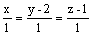
плоскость 2y + z = 0
плоскость 4(y + 2) + 5(z + 1) = 0
Данная поверхность 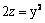 является
является
параболическим цилиндром
гиперболическим параболоидом
эллиптическим параболоидом
гиперболическим цилиндром
Данная поверхность 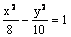 является
является
гиперболическим цилиндром
двухполостным гиперболоидом
однополостным гиперболоидом
эллиптическим цилиндром
Вектор 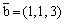
перпендикулярен прямой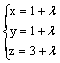
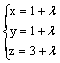
параллелен прямой 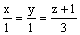
параллелен плоскости x + y + 3z -1 = 0
перпендикулярен плоскости 2(x - 1) + 4(y - 1) + (z - 3) = 0
На плоскости Oxy уравнением прямой по точке M0(x0, y0) и нормальному вектору 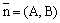 является уравнение
является уравнение
A(x - x0) + B(y - y0) = 0
Гиперболоид 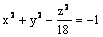 является
является
линейчатой поверхностью
поверхностью вращения вокруг оси Ox
поверхностью вращения вокруг оси Oy
поверхностью вращения вокруг оси Oz
Уравнением (z + 2)(z - 3) = 0 задается вырожденная поверхность второго порядка, представляющая собой
пустое множество
точку
прямую
две параллельные плоскости
Данная поверхность 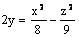 является
является
эллиптическим параболоидом
конусом
гиперболическим параболоидом
гиперболическим цилиндром
Данная поверхность 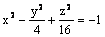 является
является
гиперболическим цилиндром
двухполостным гиперболоидом
эллипсоидом
однополостным гиперболоидом