Математическая логика и теория алгоритмов
Автомат, однократно считывающий входную строку слева направо, называется
конечным
дискретным
элементарным
МП-автоматом
В своей самой первой работе по нечетким множествам Л. Заде предложил два нечетких множества
операторы максимума для пересечения объединения
оператор минимума для объединения и оператор максимума для пересечения
оператор минимума для пересечения и оператор максимума для объединения
операторы минимума для пересечения объединения
Множество всех истинных утверждений языка L является
неразрешимым, но перечислимым
разрешимым и перечислимым
разрешимым, но неперечислимым
неразрешимым и неперечислимым
Примером логического парадокса может служить
парадокс Рассела
парадоксы лжеца и Берри
парадокс лжеца
парадокс Берри
Логическая связка конъюнкция высказываний А и В обозначается как
В 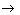 А
А
А 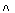 В
В
А 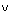 В
В
А 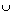 В
В
Логику можно разделить на формальную и
математическую
логику высказываний
логику Буля
логику предикатов
Если 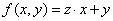 и рекурсия проводится по переменной
и рекурсия проводится по переменной 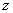 , то функция
, то функция 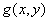 равна
равна
Символы, которые машина Тьюринга читает и пишет на ленте, образуют
выражения
алфавит
конфигурацию
команды
Нечеткая логика - это надмножество
модальной логики
логики высказываний
математической логики
логики Буля
Последовательное применение ряда формул теории, такое, что любая формула этого ряда есть либо аксиома этой теории, либо непосредственное следствие из применения предыдущих формул, называется
выводом
выражением
парадоксом
отношением
Система теоретико-множественных операций над высказываниями, которые являются элементами множества, называется
логика высказываний
система высказываний
алгебра высказываний
теория высказываний
Существуют три основных класса фраз: имена, предложения и
кванторы
предикаты
дизъюнкты
функторы
Семантические парадоксы еще называют
эпистемологическими
порадоксами теории множеств
порадоксами Рассела
логическими
Формула в теории, для которой существует механизм вывода в рамках этой теории, называется
разрешимая
выводимая
неразрешимая
не выводимая
Нечеткое отношение - это заданное определенным образом
произведение
отображение
высказывание
отношение
К термам лингвистической переменной предъявляется лишь требование
истинности
упорядоченности
не противоречивости
не отрицательности
Раздел математики, объектом изучения которого являются математические абстракции программ, выполненных на определенных алгоритмических языках и обладающих определенной информационной и логической структурой, называется
математический анализ
неевклидова геометрия
теоретическое программирование
математическое программирование
Если A рекурсивно, а B - рекурсивно перечислимо, то _____ рекурсивно
Декартово произведение - это операция над
нечеткими множествами
лингвистическими переменными
нечеткими высказываниями
множествами
Множество А есть подмножество В в том и только в том случае, если каждый элемент множества А является также
элементом множества
является другим множеством
является элементом другого множества
не является элементом множества
Базовая единица языка, обладающая определенной для данного языка синтаксической и смысловой законченностью и выражающая утверждение, называется
предложение
подмножество
слово
выражение
Выражение «множество А содержится в множестве В» записывается как
А / В
А Ì В
А 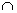 В
В
А 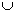 В
В
Всякое непустое ______ множество является _________ некоторой всюду определенной вычислимой функции
рекурсивное, областью определения
продуктивное, множеством значений
креативное, областью определения
рекурсивно перечислимое, множеством значений
Формальная грамматика, позволяющая построить любую правильную цепочку символов, называется грамматикой
автоматной
порождающей
регулярной
нормальной
Установление соответствия между элементарными высказываниями формальной теории и содержательными высказываниями некоторой предметной области называется
интерпретацией теории
эффективной процедурой
порождающей грамматикой
классом функторов
Выражением называется
внутреннее состояние
конечная последовательность символов
исходная ситуация
набор команд
Создателем формальной логики был
Кантор
Аристотель
Евклид
Лейбниц
Часть логики, в которой для решения логических задач используется язык математических и логических знаков, - это
логика предикатов
логика высказываний
логика Буля
математическая логика
Функция 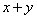 является: 1) частично вычислимой; 2) примитивно рекурсивной; 3) частично рекурсивной
является: 1) частично вычислимой; 2) примитивно рекурсивной; 3) частично рекурсивной
1
1 и 2
1 и 3
2 и 3
Не сохраняет примитивную рекурсивность оператор
подстановки
сдвига
рекурсии
минимизации
Множество натуральных чисел является
только рекурсивным
только перечислимым
простейшим
рекурсивным и перечислимым
Интуитивное представление о «вычислительной процедуре» существовало давно, и за этими процедурами был закреплен специальный термин
алгоритм
множество
высказывание
парадокс
Способ выбора подкласса истинных высказываний, принадлежащих классу элементарных высказываний, - это
теория
предложение
выражение
теорема
Науки, в которых преобладают дедуктивные рассуждения, принято называть
гуманитарными
техническими
естественно-научными
точными
Конечному автомату соответствует грамматика, порождающая
словарь машины
язык программирования
регулярный язык
машину Тьюринга
Высказывания и высказывательные формы называются
отношениями
формулами
выводами
выражениями
В логике принято делить рассуждения на
индуктивные и предикативные
дедуктивные и предикативные
индуктивные и дедуктивные
дедуктивные и информационные
Каждая п.р.ф имеет число номеров
индивидуальное
бесконечное
небольшое
ограниченное
Команда машины Тьюринга состоит из элементарных действий
любого числа
трех
конечного числа
двух
Теория, содержащая два вида правил, называемых правилами образования и правилами преобразования, называется
аксиоматическая теория
теория множеств
теория парадоксов
дедуктивная теория
Конечное множество команд, имеющих попарно различные начальные пары символов, называется
алгоритмом
конфигурацией
машиной Тьюринга
программой