Временные ряды и динамические процессы
Спектральная плотность связана с интенсивностью согласно формуле
Процесс АР(2) имеет автокорреляционную функцию, которая
имеет бесконечную протяженность
не меняется после 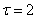
обращается в ноль после некоторой точки
имеет максимум в точке 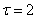
Сглаживание временного ряда означает устранение
функции тренда
сезонной компоненты
циклической компоненты
случайных остатков
О наличии данной частоты в спектре временного ряда свидетельствует ________ спектральной плотности
минимум
пик на графике
обращение в ноль
быстрые осцилляции
В критерии серий, основанном на медиане, временному ряду 2, 5, 4, 6, 3 соответствует последовательность
Для выполнения теста Чоу используется распределение
Фишера
Стьюдента
Гаусса
Пуассона
В методе скользящего среднего веса определяется с помощью ______
критерия серий, основанного на медиане
метода последовательных разностей
МНК
критерия восходящих и нисходящих серий
Идентификация модели СС(2) сводится к решению системы двух ______ уравнений
тригонометрических
дифференциальных
нелинейных
линейных
Модель Кейгана - модель, описывающая гиперинфляцию с помощью модели
скользящего среднего
адаптивных ожиданий
частичного приспособления
потребления
Для конечного процесса авторегрессии порядка 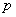 величина e
величина e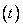 может быть представлена как ____ сумма предшествующих
может быть представлена как ____ сумма предшествующих 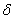
бесконечная
расходящаяся
конечная
ограниченная
Если элементы набора данных не являются статистически независимыми, то речь идет о
случайной выборке
временном ряде
стационарном временном ряде
генеральной совокупности
Лаговая структура Койка описывает простую экономическую ситуацию, когда влияние 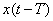 на
на 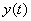 с увеличением
с увеличением 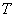
проходит через максимум
равномерно уменьшается
проходит через минимум
не изменяется
Критерий восходящих и нисходящих серий позволяет
выявить неслучайную составляющую
найти доверительный интервал прогноза
определить среднеквадратичное отклонение
найти минимальные и максимальные значения
Порядок модели Бокса - Дженкинса подбирается c помощью анализа поведения функции
спектральной плотности 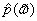
дисперсии 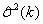
интенсивности 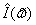
автоковариации 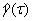
Если неслучайная составляющая временного ряда 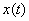 имеет линейный вид
имеет линейный вид  , то
, то 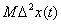 равно
равно
Обычно прогнозы, получаемые с помощью моделей Бокса - Дженкинса, оказываются на практике _______________ прогнозов, построенных по макроэкономическим моделям
не лучше
значительно лучше
значительно хуже
не хуже
Для идентификации АР и СС моделей сначала делают оценки
частной автокорреляции
автокорреляционной функции
спектральной плотности
автоковариационной функции
Коэффициент автокорреляции 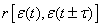 случайных остатков в модели АР(1) равен
случайных остатков в модели АР(1) равен
Неслучайная составляющая аппроксимируется полиномом степени p, если функция 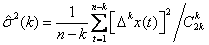
не меняется после 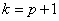
перестает возрастать после 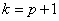
обращается в ноль в точке 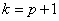
имеет пик в точке 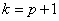
В критерии восходящих и нисходящих серий временному ряду 6, 2, 4, 6, 4 соответствует последовательность
Если временной ряд является стационарным в узком смысле, то
Процесс СС(2) имеет автокорреляционную функцию, которая
имеет бесконечную протяженность
имеет максимум в точке 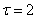
обращается в ноль после некоторой точки
не меняется после 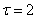
Коэффициент Тейла служит критерием
успешности сделанного прогноза
применимости статистических методов
стационарности временного ряда
сходимости временного ряда
В критерии серий, основанном на медиане, протяженность самой длинной серии временного ряда 5, 1, 4, 2 равна
4
1
3
2
Если коэффициент Тейла равен нулю, то
следует провести повторные измерения
в данном случае он неприменим
прогноз сделан неудачно
прогноз сделан успешно
Функция спектральной плотности позволяет установить
успешность сделанного прогноза
стационарность временного ряда
дисперсию временного ряда
частоты колебаний
В критерии серий, основанном на медиане, общее число серий временного ряда 1, 3, 5, 4, 2 равно
4
5
3
2
Для стационарных временных рядов при 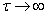 величина
величина 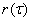
не определена
стремится к единице
осциллирует
стремится к нулю
Зависимость объемов введенных основных фондов от капитальных вложений описывается
регрессионной моделью с распределенными лагами
авторегрессионной моделью 2-го порядка
моделью скользящего среднего 2-го порядка
моделью Бокса - Дженкинса
На больших временах ________факторы описываются монотонной функцией
долговременные
случайные
сезонные
циклические
Целевая переменная в модели частичного приспособления имеет вид
Если неслучайная составляющая временного ряда 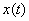 имеет вид полинома 3-й степени, то
имеет вид полинома 3-й степени, то 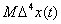 равно
равно
Критерий серий, основанный на медиане, позволяет
найти доверительный интервал предсказания
определить успешность прогноза
определить выборочное среднее
выявить неслучайную составляющую
Для весовых коэффициентов в методе скользящего среднего справедлива формула
Спектральная плотность временного ряда определяется через
частную автокорреляционную функцию 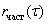
автоковариационную функцию 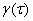
автокорреляционную функцию 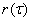
автоковариационную функцию, взятую в нуле 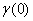
Ряд 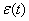 , сгенерированный моделью СС(1), может быть представлен также в виде модели авторегрессии _________ порядка
, сгенерированный моделью СС(1), может быть представлен также в виде модели авторегрессии _________ порядка
бесконечного
нулевого
второго
первого