Временные ряды и динамические процессы
Коэффициент Тейла лежит в пределах
от 0 до 1
от 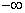 до
до 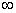
от 0 до 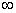
от -1 до 1
Если в ряде содержится скрытая гармоника частоты 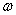 , то в нем присутствуют также периодические члены с частотой
, то в нем присутствуют также периодические члены с частотой
Аналитические методы выделения неслучайной составляющей основаны на допущении, что
дисперсия случайных остатков равна нулю
известен общий вид неслучайной составляющей
известны полиномиальные коэффициенты неслучайной составляющей
временной ряд является стационарным
Если неслучайная составляющая 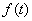 описывается полиномом степени
описывается полиномом степени 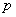 , то в методе МНК возникает ___ уравнений
, то в методе МНК возникает ___ уравнений
p - 1
p+1
p
2p
Условие стационарности ряда случайных остатков в модели АР(1) имеет вид
Исследование соотношения между спросом на реальные денежные остатки и ожидаемым изменением уровня цен описывается моделью
Алмон
Кейгана
Койка
Линтнера
Когда делается предсказание на момент времени 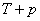 , предполагается, что известна величина
, предполагается, что известна величина
Автокорреляционная функция принимает значения в пределах
от 0 до 1
от -1 до 1
от 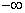 до
до 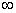
от 0 до 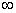
В модели Линтнера реальный объем дивидендов подвергается корректировке
В критерии восходящих и нисходящих серий проверяется гипотеза
Если элементы набора данных не являются одинаково распределенными, то речь идет о
временном ряде
генеральной совокупности
стационарном временном ряде
случайной выборке
Подбор порядка аппроксимирующего полинома производится при помощи
метода наименьших квадратов
метода последовательных разностей
анализа графика спектральной плотности