Основные понятия математической статистики
Дан вариационный ряд выборки объема n = 7: -5, -3, 0, 1, 1, 4, 16. Выборочная медиана d и выборочное среднее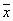 
для этого ряда равны
для этого ряда равныd = 1;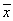 
= 2
= 2d = 5; 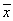= 2
= 2d = 2,5; 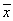= 1
= 1d = 1; 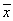= 1
= 1Доверительный интервал для среднего считается по следующей формуле:
Распределение выборки рабочих по времени, затраченному на обработку одной детали, приведено в таблице: 
Эмпирическое среднее времени, затрачиваемого на обработку одной детали, эмпирическая дисперсия и среднеквадратическое отклонение равны
Эмпирическое среднее времени, затрачиваемого на обработку одной детали, эмпирическая дисперсия и среднеквадратическое отклонение равны7,5; 4,56; 2,14
7,1; 4,08; 2,02
7,442; 4,12; 2,03
7,4; 4,24; 2,06
Дано статистическое распределение выборки с числом вариантов m. Центральный момент k-ого порядка находится по формуле:
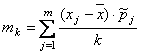
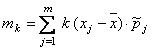
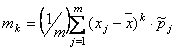
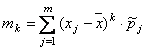
Величина x имеет распределение N(a, s). Вероятность p{x < a - 2s} равна
0,954
0,977
0,046
0,023
Величина x имеет распределение N(a, s). Вероятность p{|x - a| < 2s} равна
0,977
0,997
0,023
0,954
В таблице статистического распределения, построенного по выборке, на одно число попала клякса. 
Это число:
Это число:х = 0,4
х = 0,2
х = 0,5
х = 0,3
Случайная величина X распределена «нормально с параметрами 0,1» - N[0,1]. Вероятность для нее попасть внутрь интервала [-3,3] равна
0.8
0.68
0.95
0.9973
Доверительный интервал для вероятности успеха в схеме Бернулли для выборки с возвратом считается по следующей формуле:
, где 
, где 
, где 
, где Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема nх = 42 и ny = 20 с такими характеристиками: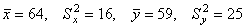 
. При уровне значимости a=0.05 проверяется гипотеза о равенстве генеральных средних mx=my (конкурирующая гипотеза mx≠my). Опытное значение статистики Т, применяемой для проверки гипотезы Н0, равно
. При уровне значимости a=0.05 проверяется гипотеза о равенстве генеральных средних mx=my (конкурирующая гипотеза mx≠my). Опытное значение статистики Т, применяемой для проверки гипотезы Н0, равно3.85
4.5
5.0
4.16
Дан вариационный ряд выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12. Выборочная медиана для этого ряда -d равна
4
5
3
4,5
Для нахождения по плотности вероятности f(x) вероятности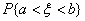 
попаданий случайной величины x в интервал (а, b) формула имеет следующий вид:
попаданий случайной величины x в интервал (а, b) формула имеет следующий вид:
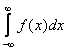
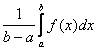
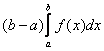
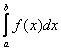
Из генеральной совокупности извлечена выборка и составлена таблица эмпирического распределения: 
Точечная оценка генеральной средней составит
Точечная оценка генеральной средней составит3
2
4
5
Вероятность выиграть, играя в рулетку, 1/37. Сделав ставку 100 раз, мы ни разу не выиграли. Заподозрив, что игра ведется нечестно, мы решили проверить свою гипотезу, построив 95%-ый доверительный интервал. Определите, по какой формуле строится интервал и что дала проверка в нашем случае
, игра нечестная
, игра честная, игра нечестная
, игра честнаяДана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее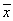
возрастет в 5 раз и выборочная дисперсия S2 возрастет в 5 раз
возрастет в 5 раз, а выборочная дисперсия S2 увеличится в 25 раз
возрастет в 5 раз, а выборочная дисперсия не изменится
возрастет в 25 раз, а выборочная дисперсия S2 увеличится в 5 раз
Дан вариационный ряд выборки объема n = 10: -2, 0, 3, 3, 4, 5, 9, 11, 12, 15. Выборочная медиана для этого ряда -d равна
4
6
4,5
5
Монету бросали 100 раз. 62 раза выпал орел; для проверки гипотезы о симметричности монеты строим 95%-ый доверительный интервал для р и проверяем, попали ли мы в него. Определите, по какой формуле строится доверительный интервал и что даст проверка в нашем конкретном случае
, симметричная
, не симметричная, симметричная
, не симметричнаяПо выборке построена статистическая таблица распределения.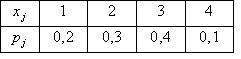 
Значение выборочной медианы
Значение выборочной медианыd = 1,5
d = 3,5
для ее определения не хватает данных
d = 2,5
В итоге четырех измерений некоторой физической величины одним прибором получены следующие результаты: 8, 9, 11, 12. Выборочная средняя результатов измерений, выборочная и исправленная дисперсии ошибок прибора равны
9; 2,5; 3,(3)
10; 25; 5
9; 25; 5
10; 2,5; 3,(3)
Для упрощения счета из всех значений выборки вычли 1280. Эмпирическая дисперсия при этом
уменьшится в 1280 раз
не изменится
уменьшится на 1280
увеличится в 1280 раз
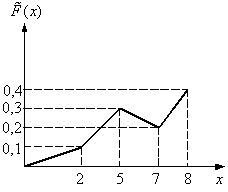
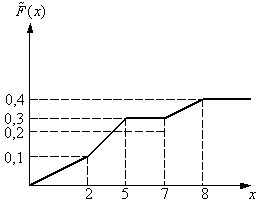
Дано статистическое распределение выборки: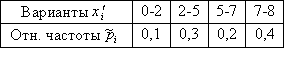 
График кумуляты для этой выборки имеет вид:
График кумуляты для этой выборки имеет вид: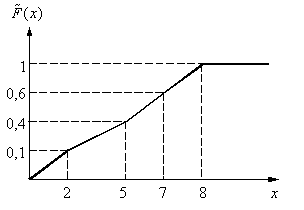
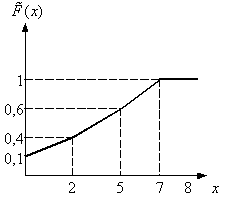
Производится выборка объема n = 100 из генеральной совокупности, имеющей распределение N(20,4). По выборке строится выборочное среднее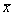 
. Эта случайная величина имеет распределение
. Эта случайная величина имеет распределениеN(20; 4)
N(20; 0,04)
N(20; 0,4)
N(0,2; 0,04)
В таблице статистического распределения, построенного по выборке, одна цифра написана неразборчиво. 
Это цифра:
Это цифра:х = 3
х = 2
х = 5
х = 4
Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема nх = 42 и ny = 20 с такими характеристиками: 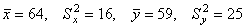. При уровне значимости a = 0.05 проверяется гипотеза о равенстве генеральных средних mx=my (конкурирующая гипотеза mx≠my). Область принятия гипотезы Н0, равна
. При уровне значимости a = 0.05 проверяется гипотеза о равенстве генеральных средних mx=my (конкурирующая гипотеза mx≠my). Область принятия гипотезы Н0, равна(-2, 2)
(-1.8, 1.8)
(-3, 3)
(-2.5, 2.5)
Дана выборка объема n = 10. Статистическое распределение этой выборки имеет вид: 
Тогда выборочное среднее 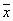для этой выборки равно
Тогда выборочное среднее для этой выборки равно=3,3=3,0=4,0=3,4Правильным является следующее соотношение:
M(X - Y) = M(X) - M(Y)
M(X - Y) = M(X) + M(Y)
По выборке построен доверительный интервал для генерального среднего. Оказалась, что генеральное среднее по такому объему выборки определяется с точностью 0,2. Чтобы повысить точность вдвое, объем выборки надо
увеличить в 4 раза
увеличить в 8 раз
уменьшить в 2 раза
увеличить в 2 раза
Случайная величина распределена равномерно на отрезке [0, 2]. Ее математическое ожидание и дисперсия равны
1; 1/3
0; 1/3
0,5; 1/12
1; 1/12
Дана выборка объема n: х1, х2, …, хn. Статистический (или эмпирический) начальный момент k-го порядка находится по следующей формуле:
ak =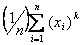 
ak =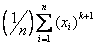 
ak =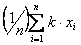 
ak =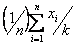 
По выборке объема n из нормального распределения с неизвестной дисперсией строится доверительный интервал для математического ожидания. Объем выборки увеличиваем в 16 раз. В предположении, что величины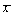 
и S2 при этом изменятся мало, длина доверительного интервала примерно
и S2 при этом изменятся мало, длина доверительного интервала примерноуменьшится в 4 раза
увеличится в 4 раза
увеличится в 16 раз
уменьшится в 16 раз
Формула M(X + Y) = M(X) + M(Y) верна
только для положительных Х и Y
всегда
только для отрицательных Х и Y
только для независимых X и Y
Дана выборка объема n: х1, х2, …, хn. Выборочная средняя равна 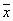. Тогда статистический центральный момент k-го порядка находится по следующей формуле:
. Тогда статистический центральный момент k-го порядка находится по следующей формуле:
Правильным является следующее соотношение:
D(-2X) = 4D(X)
D(-2X) = 2D(X)
D(-2X) = -4D(X)
D(-2X) = -2D(X)
Дано статистическое распределение выборки: 
Выборочное среднее 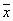и выборочная дисперсия S2 равны
Выборочное среднее и выборочная дисперсия S2 равны= 2, S2 = 17,6= 3, S2 = 53= 2, S2 = 4,4= 3, S2 = 6,5Выборочное распределение задано таблицей. 
Значение кумуляты в точке 170 и медиана, вычисленные по этой таблице, равны
Значение кумуляты в точке 170 и медиана, вычисленные по этой таблице, равны0,65; 168;
0,9; 170;
0,5; 166;
0,8; 166;
Дана выборка объема n = 10: 0, 2, 3, 5, 5, 6, 6, 7, 8, 9. Выборочное среднее равно
Дана выборка объема n = 5: 2, 3, 5, 7, 8. Выборочное среднее 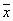и выборочная дисперсия S2 равны
и выборочная дисперсия S2 равны
Для того, чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить в ___ раз(а)
4
2
8
16
Дан вариационный ряд выборки объема n = 8: -2, 0, 3, 4, 6, 9, 12, 16. Выборочная медиана d и выборочное среднее 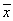для этого ряда равны
для этого ряда равныd = 5; 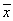= 5
= 5d = 4; 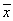= 5
= 5d = 6; 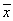= 6
= 6d = 5; 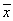= 6
= 6Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения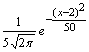 
, равны
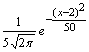, равны2; 5
2; 1
0; 5
2; 25