Математика (курс 10)
Если функция 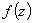 удовлетворяет соотношениям
удовлетворяет соотношениям 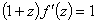 и
и 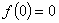 , то в окрестности точки z = 0 она разлагается в ряд
, то в окрестности точки z = 0 она разлагается в ряд
Функция 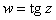 аналитична всюду в С, кроме точек
аналитична всюду в С, кроме точек
Функция 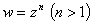 преобразует сектор
преобразует сектор 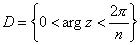 в
в
плоскость w
плоскость w с выброшенным отрезком 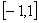
плоскость w с выброшенной положительной полуосью
верхнюю полуплоскость
Дробно-линейное отображение, переводящее единичный круг в единичный круг и отличное от тождественного, имеет вид
Если функция 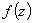 - четная те
- четная те 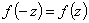 и точка
и точка 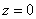 является изолированной особой точкой этой функции то
является изолированной особой точкой этой функции то  равен
равен
-1
0
1
Пусть координаты стереографической проекции точки z = x + iy есть 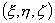 ; тогда координаты стереографической проекции точки
; тогда координаты стереографической проекции точки 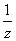 есть
есть
Функция 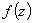 называется аналитической в точке
называется аналитической в точке 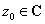 , если она дифференцируема в смысле
, если она дифференцируема в смысле
С в некоторой окрестности этой точки
С в этой точке
Если 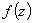 и
и 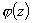 - функции аналитические в точках замкнутой кусочно-гладкой кривой
- функции аналитические в точках замкнутой кусочно-гладкой кривой 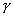 и внутри нее и если в точках этой кривой
и внутри нее и если в точках этой кривой 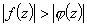 , то внутри
, то внутри 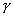 число нулей функции
число нулей функции 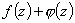 равно
равно
числу нулей функции 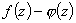
числу нулей функции 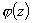
нулю
числу нулей функции 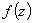
Для функции 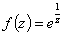 точка
точка 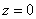 является
является
полюсом
устранимой
существенной особой точкой
неизолированной особой точкой
Какая из нижеперечисленных функций дифференцируема в смысле С
Для коэффициентов ряда Тейлора функции 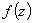 справедлива оценка (
справедлива оценка (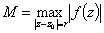
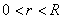 R - радиус сходимости ряда):
R - радиус сходимости ряда):
Для однолистности отображения 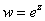 в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек
в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек 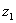 и
и 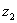 , связанных соотношением
, связанных соотношением
Если функция 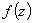 удовлетворяет соотношениям
удовлетворяет соотношениям 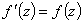 и
и 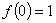 , то в окрестности точки z = 0 она разлагается в ряд
, то в окрестности точки z = 0 она разлагается в ряд
Если функция 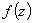 в окрестности полюса а первого порядка представима в виде
в окрестности полюса а первого порядка представима в виде 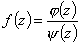 где
где 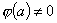 и
и 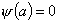
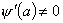 , то ее вычет в точке а вычисляется по формуле
, то ее вычет в точке а вычисляется по формуле
Для функции 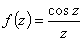 точка
точка 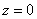 является
является
устранимой
существенной особой точкой
полюсом
неизолированной особой точкой
Для того чтобы функция 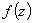 определенная в окрестности точки
определенная в окрестности точки 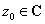 имела в этой точке производную необходимо и достаточно чтобы
имела в этой точке производную необходимо и достаточно чтобы
Мероморфная функция с полюсом в бесконечности является
рациональной
постоянной
полиномом
ограниченной
Согласно теореме о полной сумме вычетов имеет место равенство (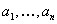 - конечные изолированные особые точки функции
- конечные изолированные особые точки функции 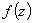 ):
):
Для однолистности отображения 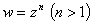 в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек
в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек 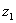 и
и 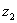 , связанных соотношением
, связанных соотношением
Для однолистности отображения 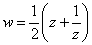 в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек
в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек 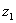 и
и 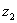 , связанных соотношением
, связанных соотношением
Дробно-линейное отображение, переводящее верхнюю полуплоскость 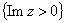 в единичный круг
в единичный круг 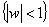 имеет вид
имеет вид
Сопряженным с комплексным числом x + iy называется число вида
x + iy
y - ix
x - iy
y + ix
Пусть координаты стереографической проекции точки z = x + iy есть 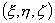 ; тогда координаты стереографической проекции точки - z есть
; тогда координаты стереографической проекции точки - z есть
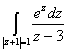 равен
равен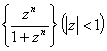 равен
равен