Предел и непрерыв-ность функции одной переменной
Переменная величина 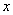 является бесконечно большой (б.б.), если
является бесконечно большой (б.б.), если
для 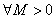 , начиная с некоторого момента в изменении
, начиная с некоторого момента в изменении 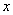 выполняется неравенство
выполняется неравенство 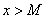
Во всех точках некоторого интервала 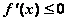 . Тогда
. Тогда 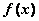 на этом интервале
на этом интервале
убывает
не убывает
не возрастает
монотонно убывает
Вертикальной асимптотой графика функции 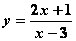 является прямая
является прямая
Последовательность может иметь
два различных предела
только один предел
любое количество пределов
не больше двух разных пределов
Если 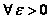
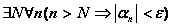 , то
, то 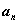
бесконечно большая
меньшего порядка малости 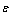
бесконечно малая
стремится к 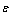
Переменная величина 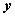 есть функция переменной величины
есть функция переменной величины 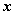 , если
, если
между значениями величин 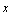 и
и 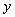 установлено взаимно однозначное соответствие
установлено взаимно однозначное соответствие
каждому значению 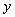 отвечает определенное значение
отвечает определенное значение 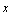
каждому значению 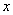 по некоторому правилу поставлено в соответствие определенное значение
по некоторому правилу поставлено в соответствие определенное значение 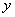
каждому значению 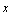 отвечает определенное значение
отвечает определенное значение 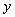 и каждому значению
и каждому значению 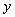 отвечает некоторое определенное значение
отвечает некоторое определенное значение 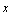
Число p изображается десятичной дробью
бесконечной
периодической
бесконечной непериодической
конечной
Взаимно однозначное соответствие между точками числовой оси и действительными числами означает, что
все действительные числа лежат на оси
положительные и отрицательные целые числа являются координатами точек оси
все рациональные числа изображаются точками оси
каждая точка оси изображается действительным числом - своей координатой и каждое действительное число оказывается координатой определенной точки
Необходимым условием существования экстремума функции 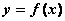 в точке
в точке 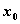 является условие
является условие
порядок 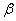 выше
выше
Теорема Лагранжа верна, если функция 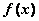
непрерывна и дифференцируема на 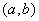
непрерывна на 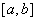 и дифференцируема по крайней мере на
и дифференцируема по крайней мере на 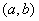
непрерывна на 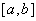
дифференцируема на 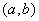
Даны определения: 1) всякая монотонная ограниченная последовательность имеет предел; 2) последовательность 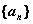 называется монотонной, если она является убывающей; 3) последовательность
называется монотонной, если она является убывающей; 3) последовательность 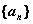 называется невозрастающей, если
называется невозрастающей, если 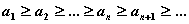 ; 4) последовательность
; 4) последовательность 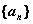 является возрастающей, если
является возрастающей, если 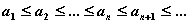
1
3, 4
2, 3
1, 3
Последовательность  является б.м. потому, что
является б.м. потому, что
Последовательность 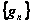 , при
, при  является
является
ограниченной
бесконечно большой
бесконечно малой
неограниченной
для любого 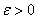 найдется такое
найдется такое 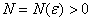 , что при
, что при 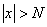 имеет место неравенство
имеет место неравенство 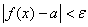 , т.е. при любом
, т.е. при любом 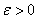 можно найти такое
можно найти такое 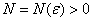 , что при
, что при 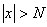 значения
значения 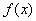 попадают в
попадают в 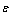 -полосу, построенную вокруг прямой
-полосу, построенную вокруг прямой 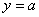
при некотором 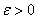 значения
значения 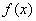 находятся в
находятся в 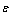 -полосе вокруг прямой
-полосе вокруг прямой 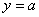
при 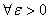 выполняется неравенство
выполняется неравенство 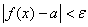
значения 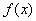 находятся в
находятся в 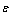 -полосе вокруг прямой
-полосе вокруг прямой 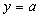
Положение точки 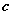 , о которой говорится в теоремах Лагранжа, Ролля, Коши, находится
, о которой говорится в теоремах Лагранжа, Ролля, Коши, находится
в точке 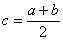
в одном из концов интервала
где-то между 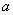 и
и 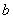 :
: 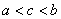
на середине отрезка 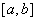
бесконечно малая высшего порядка в сравнении с 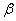
является бесконечно малой
Функция 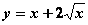 на интервале (0, 4)
на интервале (0, 4)
имеет минимум
монотонно убывает
имеет максимум
монотонно возрастает
Для функции 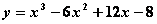 точка М(2, 0) является точкой
точка М(2, 0) является точкой
максимума
минимума
перегиба
разрыва
Стационарной точкой функции 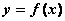 является точка
является точка 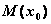 в которой
в которой
Интервалами монотонности функции 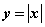 будут:
будут:
один интервал 
График функции 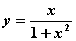
асимптот (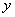 ) не имеет, так как знаменатель не обращается в нуль
) не имеет, так как знаменатель не обращается в нуль
имеет единственную асимптоту: 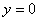
имеет асимптоту: 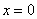
не имеет точек разрыва и асимптот
Свойство инвариантности формы записи дифференциала функции 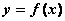 означает, что
означает, что
дифференциал 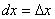
форма записи дифференциала 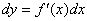 не зависит от того, будет ли
не зависит от того, будет ли 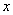 независимой переменной или функцией
независимой переменной или функцией 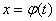 от другой переменной
от другой переменной
форма записи дифференциала 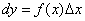 сохраняется, когда
сохраняется, когда 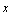 перестает быть независимой переменной
перестает быть независимой переменной
во всех случаях дифференциал является главной частью приращения функции
С помощью логических символов определение предела последовательности 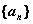 выражается так
выражается так
при 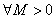 будет
будет 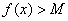
значения 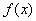 очень велики
очень велики
для любого 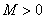 найдется
найдется 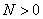 такое, что при
такое, что при 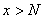 выполняется неравенство
выполняется неравенство 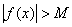 ; иначе говоря
; иначе говоря 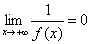
для 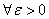
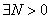 такое, что при
такое, что при 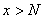 выполняется неравенство
выполняется неравенство 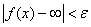
Число 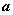 есть предел функции
есть предел функции 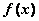 при
при 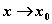 , если
, если
для 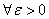
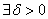 такое, что при всех
такое, что при всех 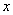 , попавших в
, попавших в 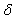 -окрестность точки
-окрестность точки 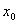 , выполняется неравенство
, выполняется неравенство 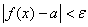
при 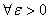 значение
значение 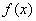 лежит в
лежит в 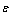 -окрестности числа
-окрестности числа 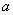
для 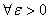 выполняется неравенство
выполняется неравенство 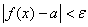
для любого 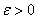 найдется
найдется 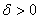 такое, что при всех
такое, что при всех 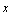 , попадающих в
, попадающих в 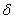 -окрестность точки
-окрестность точки 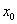 , кроме, быть может,
, кроме, быть может, 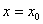 , выполняется неравенство
, выполняется неравенство 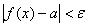
На интервале 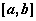 непрерывная функция
непрерывная функция 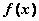 имеет единственную точку максимума
имеет единственную точку максимума 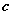 ,
, 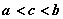 , и не имеет других точек экстремума. Ее наименьшее значение на
, и не имеет других точек экстремума. Ее наименьшее значение на 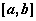 будет
будет
либо 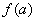 , либо
, либо 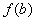
при 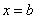
при 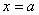
в критической точке
Число 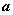 есть предел переменной величины
есть предел переменной величины 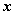 , если
, если
значения 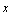 лежат в интервале
лежат в интервале 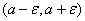
значения 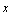 лежат в
лежат в 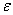 -окрестности
-окрестности 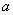
какое бы (сколь угодно малое) число 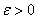 мы ни взяли, начиная с некоторого момента в изменении
мы ни взяли, начиная с некоторого момента в изменении 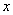 будет выполняться неравенство
будет выполняться неравенство 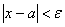
выполняется неравенство 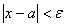
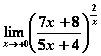 равен
равен