Математический анализ (курс 5)
Числовая ось - это прямая, на которой
установлено направление
отсчитываются длины
выбрано начало отсчета
выбрано начало отсчета, установлены направление и единица измерения длин
Действительные числа - это
числа, которые действительно существуют
целые числа
положительные числа
рациональные и иррациональные, положительные и отрицательные числа и число нуль
Для функции 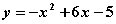 точка М (3, 4) является точкой
точка М (3, 4) является точкой
минимума
перегиба
максимума
разрыва
Переменная величина 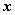 является бесконечно малой (б.м.), если
является бесконечно малой (б.м.), если
Точкой перегиба функции 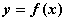 является точка
является точка 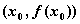 , при переходе через которую
, при переходе через которую
Любое действительное число может быть записано как десятичная дробь
конечная
периодическая
конечная и периодическая
конечная или бесконечная (периодическая или непериодическая)
Во всех точках некоторого интервала 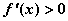 . Тогда
. Тогда 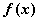 на этом интервале
на этом интервале
монотонно не убывает
возрастает
убывает
не убывает
Область значений функции 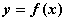 есть
есть
интервал оси 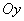
ось 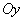
множество всех значений, принимаемых величиной 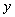
совокупность значений аргумента функции
Предел отношения приращения функции 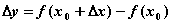 к приращению аргумента
к приращению аргумента 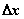 при стремлении
при стремлении 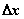 к нулю называется
к нулю называется
первообразной функцией 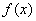
производной функции 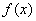
первым замечательным пределом
вторым замечательным пределом
Если 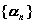 - бесконечно малая последовательность и
- бесконечно малая последовательность и 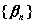 - бесконечно малая последовательность
- бесконечно малая последовательность 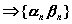 - последовательность
- последовательность
бесконечно большая
ограниченная
бесконечно малая
неограниченная
при некотором 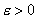 значения
значения 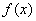 находятся в
находятся в 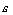 -полосе вокруг прямой
-полосе вокруг прямой 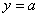
при 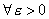 выполняется неравенство
выполняется неравенство 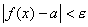
значения 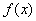 находятся в
находятся в 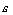 -полосе вокруг прямой
-полосе вокруг прямой 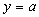
для любого 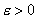 найдется такое
найдется такое 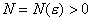 , что при
, что при 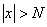 имеет место неравенство
имеет место неравенство 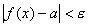 , т.е. при любом
, т.е. при любом 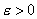 можно найти такое
можно найти такое 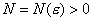 , что при
, что при 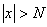 значения
значения 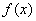 попадают в
попадают в 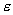 -полосу, построенную вокруг прямой
-полосу, построенную вокруг прямой 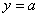
Число 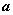 называется пределом последовательности
называется пределом последовательности 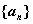 (
(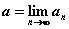 )
)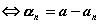 является
является
бесконечно большой
ограниченной
бесконечно малой
Функция 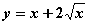 на интервале (0, 4)
на интервале (0, 4)
имеет максимум
монотонно убывает
имеет минимум
монотонно возрастает
Если 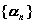 - бесконечно малая последовательность и
- бесконечно малая последовательность и 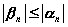 , при
, при 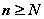
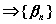 последовательность
последовательность
бесконечно малая
меньшего порядка малости
большего порядка малости
бесконечно большая
порядок 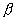 выше
выше
Для функции 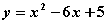 точка М (3, - 4) является точкой
точка М (3, - 4) является точкой
минимума
максимума
перегиба
разрыва
если функция 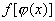 непрерывна
непрерывна
если в рассматриваемой точке 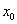 функция
функция 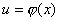 дифференцируема и функция
дифференцируема и функция 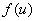 дифференцируема в точке
дифференцируема в точке 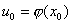
если 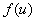 и
и 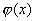 непрерывные функции
непрерывные функции
всегда
Переменная величина 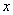 является бесконечно большой (б.б.), если
является бесконечно большой (б.б.), если
для 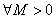 , начиная с некоторого момента в изменении
, начиная с некоторого момента в изменении 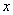 выполняется неравенство
выполняется неравенство 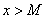
Функция 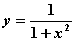 имеет интервалов монотонности -
имеет интервалов монотонности -
один
два
нет интервалов монотонности
три
Теорема Ролля верна, если функция 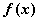
дифференцируема на 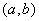 и
и 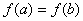
непрерывна на 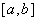 , дифференцируема на
, дифференцируема на 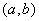 и
и 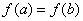
непрерывна на 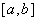 и дифференцируема по крайней мере на
и дифференцируема по крайней мере на 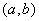
непрерывна на 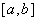 и
и 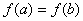
бесконечно малая высшего порядка в сравнении с 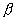
является бесконечно малой
Если 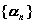 - бесконечно малая последовательность и постоянная
- бесконечно малая последовательность и постоянная 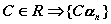 последовательность
последовательность
ограниченная
неограниченная
бесконечно малая
бесконечно большая
Число 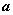 есть предел функции
есть предел функции 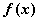 при
при 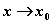 , если
, если
для 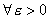 выполняется неравенство
выполняется неравенство 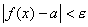
при 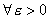 значение
значение 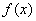 лежит в
лежит в 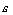 -окрестности числа
-окрестности числа 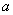
для любого 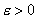 найдется
найдется 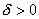 такое, что при всех
такое, что при всех 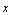 , попадающих в
, попадающих в 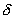 -окрестность точки
-окрестность точки 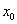 , кроме, быть может,
, кроме, быть может, 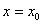 , выполняется неравенство
, выполняется неравенство 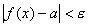
для 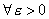
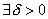 такое, что при всех
такое, что при всех 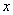 , попавших в
, попавших в 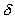 -окрестность точки
-окрестность точки 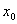 , выполняется неравенство
, выполняется неравенство 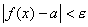
На интервале 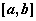 непрерывная функция
непрерывная функция 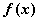 имеет единственную точку максимума
имеет единственную точку максимума 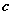 ,
, 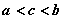 , и не имеет других точек экстремума. Ее наименьшее значение на
, и не имеет других точек экстремума. Ее наименьшее значение на 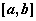 будет
будет
при 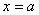
в критической точке
при 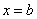
либо 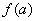 , либо
, либо 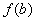
одного порядка
не сравнимы
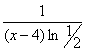
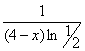
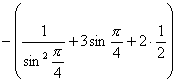
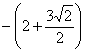
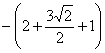
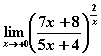 равен
равен