Вычислительная математика (курс 1)
Верны ли утверждения? Возможны следующие виды погрешностей: А) абсолютная В) округления
A – да, B – да
A – да, B – нет
A – нет, B – нет
A – нет, B – да
Метод Гаусса заключается в сведении исходной матрицы системы к эквивалентному виду, где матрица преобразованной системы является
верхней треугольной матрицей
симметричной матрицей
ленточной матрицей
диагональной матрицей
Верны ли утверждения? В виде, удобном для итераций, записаны системы линейных уравнений: А) 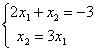 ; B)
; B) 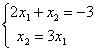 .
.
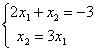 ; B)
; B) 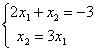 .
.A – да, B – да
A – нет, B – да
A – нет, B – нет
A – да, B – нет
Система линейных уравнений 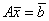 записана в виде, удобном для итераций, если она имеет вид
записана в виде, удобном для итераций, если она имеет вид
Верны ли утверждения? Возможны следующие виды матриц: А) единичная В) прямоугольная
A – нет, B – нет
A – да, B – да
A – нет, B – да
A – да, B – нет
Верны ли утверждения? Значительная потеря точности при выполнении арифметических операций на ЭВМ происходит: А) при умножении близких чисел B) при сложении близких чисел
A – да, B – нет
A – да, B – да
A – да, B – нет
A – нет, B – нет
Для линейной системы уравнений вычисления по итерационной формуле 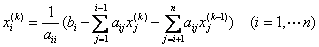 называют методом
называют методом
Зейделя
Гаусса
простой итерации
Ньютона
Дана система линейных уравнений 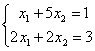 . Для сходящегося метода Зейделя ее надо записать в виде
. Для сходящегося метода Зейделя ее надо записать в виде
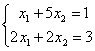 . Для сходящегося метода Зейделя ее надо записать в виде
. Для сходящегося метода Зейделя ее надо записать в виде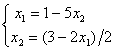
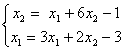
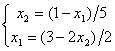
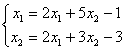
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: A) для хорошо обусловленных систем малые ошибки в задании правых частей и коэффициентов системы приводят к малым ошибкам в решении B) метод Гаусса является итерационным методом
A – нет, B – да
A – да, B – нет
A – да, B – да
A – нет, B – нет
Заданы системы линейных уравнений 1) 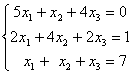 2)
2) 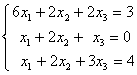 3)
3) 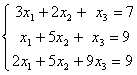 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем
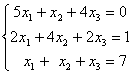 2)
2) 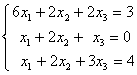 3)
3) 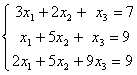 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы системтолько 3
2 и 3
только 2
1 и 2
Верны ли утверждения? Существуют следующие методы решения систем линейных уравнений А) ортогональные B) прямые
A – да, B – нет
A – нет, B – да
A – да, B – да
A – нет, B – нет
Для величин x и y заданы абсолютные погрешности Δ(x) = 0,01 и Δ(y) =1,5. Тогда абсолютная погрешность разности Δ(x−y) равна
−1,51
−1,49
1,51
1,49
Матрица A = 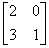 называется
называется
нижней треугольной
верхней треугольной
диагональной
верхней симметричной
Число 623 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление
6,23
0,623∙103
623
62,3
Прямой ход метода Гаусса сводит линейную систему уравнений к виду
с верхней треугольной матрицей
с трехдиагональной матрицей
с симметричной матрицей
с диагональной матрицей
Метод итераций для линейной системы 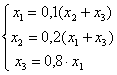
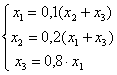
будет сходиться только при специальном выборе начального приближения
будет расходиться
будет сходиться при любом начальном приближении
приведет к зацикливанию
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: A) для плохо обусловленных систем малые ошибки в правых частях и коэффициентах приводят к большим погрешностям в решении системы B) метод Гаусса является прямым методом
A – да, B – нет
A – да, B – да
A – нет, B – нет
A – нет, B – да
Верны ли утверждения? Существуют следующие методы решения систем линейных уравнений: A) прямые B) итерационные
A – да, B – да
A – да, B – нет
A – нет, B – нет
A – нет, B – да
Верны ли утверждения? Заданы системы линейных уравнений 1) 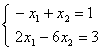 2)
2) 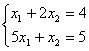 3)
3) 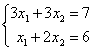 . Свойством диагонального преобладания обладают матрицы систем А) 1 B) 2 и 3
. Свойством диагонального преобладания обладают матрицы систем А) 1 B) 2 и 3
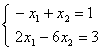 2)
2) 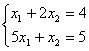 3)
3) 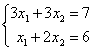 . Свойством диагонального преобладания обладают матрицы систем А) 1 B) 2 и 3
. Свойством диагонального преобладания обладают матрицы систем А) 1 B) 2 и 3A – да, B – да
A – да, B – нет
A – нет, B – нет
A – нет, B – да
Задана линейная система 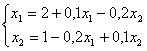 . Первое приближение метода простой итерации
. Первое приближение метода простой итерации 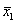 при начальном значении
при начальном значении 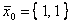 дает результат
дает результат
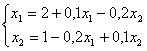 . Первое приближение метода простой итерации
. Первое приближение метода простой итерации {2; 2,7}
{2; 1}
{1,9; 0,9}
{1,9; 2,7}
Верны ли утверждения? Существуют следующие методы решения систем линейных уравнений: А) метод Гаусса В) итерационный метод Зейделя
A – да, B – нет
A – нет, B – нет
A – да, B – да
A – нет, B – да
Для величин x = 2 и y = 8 известны относительные погрешности δ(x)=0,01 и δ(y) = 0,02. Относительная погрешность суммы δ(x + y) равна
0,018
0,03
0,016
0,003
Погрешность математической модели является
возрастающей
регулируемой
вычислительной
неустранимой
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: А) метод итераций Зейделя сходится всегда B) метод простой итерации сходится, если все коэффициенты матрицы системы меньше единицы
A – да, B – нет
A – нет, B – да
A – да, B – да
A – нет, B – нет
Верны ли утверждения? Заданы системы линейных уравнений 1) 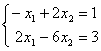 2)
2) 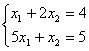 3)
3) 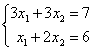 . Свойством диагонального преобладания обладают матрицы систем А) 1 и 2 B) 3
. Свойством диагонального преобладания обладают матрицы систем А) 1 и 2 B) 3
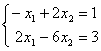 2)
2) 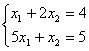 3)
3) 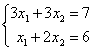 . Свойством диагонального преобладания обладают матрицы систем А) 1 и 2 B) 3
. Свойством диагонального преобладания обладают матрицы систем А) 1 и 2 B) 3A – да, B – нет
A – нет, B – да
A – нет, B – нет
A – да, B – да
Задана система линейных уравнений 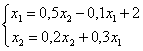 . Для заданного начального приближения x1(0) = 0; x2(0) = 1 первый шаг метода Зейделя дает следующие значения первого приближения {x1(1), x2(1)}
. Для заданного начального приближения x1(0) = 0; x2(0) = 1 первый шаг метода Зейделя дает следующие значения первого приближения {x1(1), x2(1)}
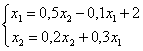 . Для заданного начального приближения x1(0) = 0; x2(0) = 1 первый шаг метода Зейделя дает следующие значения первого приближения {x1(1), x2(1)}
. Для заданного начального приближения x1(0) = 0; x2(0) = 1 первый шаг метода Зейделя дает следующие значения первого приближения {x1(1), x2(1)}{1,5; 0,2}
{2,5; 0,2}
{1,5; 0,8}
{2,5; 0,95}
Число 125,7 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление
0,1257∙103
125,7
0,01257∙104
1,257∙102
Задана система линейных уравнений 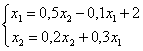 . Для заданного начального приближения x1(0) = 0; x2(0) = 1, первый шаг метода простой итерации дает следующие значения первого приближения {x1(1), x2(1)}
. Для заданного начального приближения x1(0) = 0; x2(0) = 1, первый шаг метода простой итерации дает следующие значения первого приближения {x1(1), x2(1)}
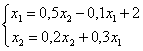 . Для заданного начального приближения x1(0) = 0; x2(0) = 1, первый шаг метода простой итерации дает следующие значения первого приближения {x1(1), x2(1)}
. Для заданного начального приближения x1(0) = 0; x2(0) = 1, первый шаг метода простой итерации дает следующие значения первого приближения {x1(1), x2(1)}{2,5; 0,5}
{2,5; 0,2}
{2,5; 0,9}
{2,5; 0,95}
Для линейной системы уравнений вычисления по итерационной формуле 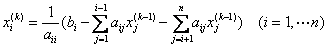 называют методом
называют методом
релаксации
простой итерации
Зейделя
Ньютона
Задана система линейных уравнений 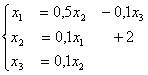 . Один шаг метода простой итерации с начальным приближением {0; 0; 0} дает следующее первое приближение
. Один шаг метода простой итерации с начальным приближением {0; 0; 0} дает следующее первое приближение
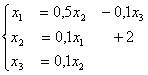 . Один шаг метода простой итерации с начальным приближением {0; 0; 0} дает следующее первое приближение
. Один шаг метода простой итерации с начальным приближением {0; 0; 0} дает следующее первое приближение{0,5; 2; 0,1}
{0; 0; 0}
{0,5; 2; 0}
{0; 2; 0}
Обобщенное решение переопределенных систем линейных уравнений (как совместных, так и несовместных) можно найти методом
интерполяции
наименьших квадратов
Зейделя
Ньютона
Заданы системы линейных уравнений 1) 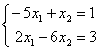 2)
2) 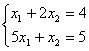 3)
3) 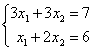 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем
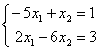 2)
2) 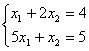 3)
3) 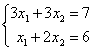 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы системтолько 2
только 3
2 и 3
1 и 3
Верны ли утверждения? В виде, удобном для итераций, записаны системы линейных уравнений А) 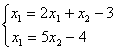 ; B)
; B) 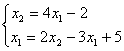 .
.
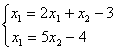 ; B)
; B) 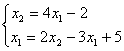 .
.A – нет, B – нет
A – да, B – да
A – да, B – нет
A – нет, B – да
Для величин x = 2 и y = 5 известны относительные погрешности δ(x)=0,005 и δ(y) = 0,002. Относительная погрешность частного δ(x ∕ y) равна
0,003
0,00001
0,0025
0,007
Заданы системы линейных уравнений 1) 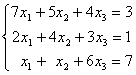 2)
2) 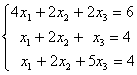 3)
3) 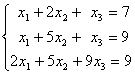 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем
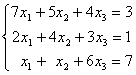 2)
2) 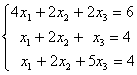 3)
3) 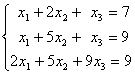 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем2
2 и 3
только 3
1 и 2
LU – разложение матрицы A представляет ее в виде
произведения верхней треугольной матрицы на диагональную матрицу
произведения симметричной матрицы на диагональную матрицу
суммы двух треугольных матриц
произведения нижней треугольной матрицы на верхнюю треугольную матрицу
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: A) итерационный метод Зейделя сходится всегда B) метод простой итерации сходится всегда
A – нет, B – нет
A – нет, B – да
A – да, B – нет
A – да, B – да
Верны ли утверждения? Возможны следующие виды матриц: А) трехдиагональная В) ленточная
A – нет, B – да
A – нет, B – нет
A – да, B – да
A – да, B – нет
Заданы системы линейных уравнений 1) 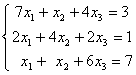 2)
2) 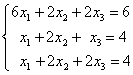 3)
3) 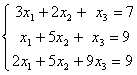 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы систем
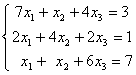 2)
2) 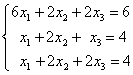 3)
3) 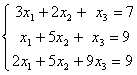 . Свойством диагонального преобладания обладают матрицы систем
. Свойством диагонального преобладания обладают матрицы системтолько 3
только 1
1 и 3
только 2
Система линейных уравнений называется переопределенной, если
правые части системы не заданы
количество уравнений системы меньше количества неизвестных
часть уравнений системы является линейными, а часть – нелинейными
коэффициенты системы заданы недостаточно точно
Дана система 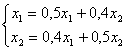 . Первое приближение для метода простой итерации с начальным приближением (0,1; 0,2) равно
. Первое приближение для метода простой итерации с начальным приближением (0,1; 0,2) равно
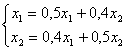 . Первое приближение для метода простой итерации с начальным приближением (0,1; 0,2) равно
. Первое приближение для метода простой итерации с начальным приближением (0,1; 0,2) равно(0,13; 0,14)
(0,9; 0,9)
(0,14; 0,13)
(0,5; 0,4)
Задана линейная система 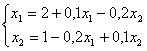 . Первое приближение метода Зейделя
. Первое приближение метода Зейделя 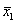 при начальном значении
при начальном значении 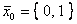 дает результат
дает результат
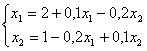 . Первое приближение метода Зейделя
. Первое приближение метода Зейделя {1,8; 0,74}
{2; 0,68}
{2; 0,74}
{1,8; 1,1}
Aбсолютные погрешности величин x и y равны Δ(x) = 0,1 и Δ(y) = 0,4. Абсолютная погрешность суммы Δ(x + y) равна
0,5
0,04
0,2
0,3
Задана система линейных уравнений 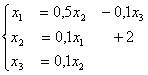 . Один шаг метода Зейделя с начальным приближением {0; 1; 0} дает следующее первое приближение:
. Один шаг метода Зейделя с начальным приближением {0; 1; 0} дает следующее первое приближение:
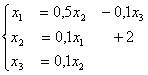 . Один шаг метода Зейделя с начальным приближением {0; 1; 0} дает следующее первое приближение:
. Один шаг метода Зейделя с начальным приближением {0; 1; 0} дает следующее первое приближение:{0,5; 2; 0,0205}
{0,3; 2,05; 2}
{0,5; 2; 0,1}
{0,5; 2,05; 0,205}
Aбсолютные погрешности величин x и y равны Δ(x) = 0,1 и Δ(y) = 0,4. Абсолютная погрешность разности Δ(x - y) равна
0,1
0,5
0,3
0,04
Для величин x = 10 и y = 20 известны относительные погрешности δ(x)=0,005 и δ(y) = 0,003. Относительная погрешность произведения δ(x ∙ y) равна
0,002
0,011
0,000015
0,008
Верны ли утверждения? Значительная потеря точности при выполнении арифметических операций на ЭВМ происходит А) при вычитании близких чисел В) при сложении близких чисел
A – да, B – да
A – нет, B – да
A – нет, B – нет
A – да, B – нет
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: А) метод итераций Зейделя сходится, если матрица системы обладает свойством диагонального преобладания B) метод простой итерации сходится, если все коэффициенты матрицы положительны
A – нет, B – да
A – да, B – да
A – нет, B – нет
A – да, B – нет
Для матрицы 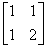 LU – разложение имеет вид
LU – разложение имеет вид
L = 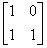 U =
U = 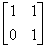
L = 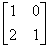 U =
U = 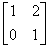
L = 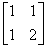 U =
U = 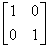
L =  U =
U =