Вычислительная математика (курс 1)
Верны ли утверждения? Даны линейные системы 1)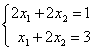 2)
2)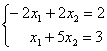 3)
3)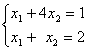 4)
4)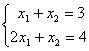 . Свойством диагонального преобладания обладают системы А) 1 и 2 В) 1 и 4
. Свойством диагонального преобладания обладают системы А) 1 и 2 В) 1 и 4
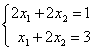 2)
2)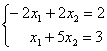 3)
3)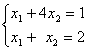 4)
4)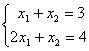 . Свойством диагонального преобладания обладают системы А) 1 и 2 В) 1 и 4
. Свойством диагонального преобладания обладают системы А) 1 и 2 В) 1 и 4A – нет, B – да
A – да, B – да
A – да, B – нет
A – нет, B – нет
Задана линейная система 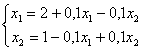 . Первое приближение метода Зейделя
. Первое приближение метода Зейделя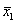 при начальном значении
при начальном значении 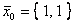 дает результат
дает результат
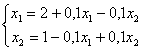 . Первое приближение метода Зейделя
. Первое приближение метода Зейделя{2; 1}
{1; 2}
{2; 0,9}
{2; 1,1}
Для матрицы A = 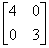 метод Зейделя x(k+1) = Ax(k) будет
метод Зейделя x(k+1) = Ax(k) будет
сходящимся
сходящимся при начальном векторе 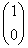
расходящимся
сходящимся при начальном векторе 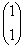
Верны ли утверждения? В виде, удобном для итераций, записаны системы линейных уравнений А) 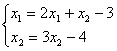 ; B)
; B) 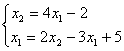 ;
;
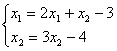 ; B)
; B) 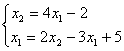 ;
;A – нет, B – нет
A – нет, B – да
A – да, B – да
A – да, B – нет
Для величин x = 2 и y = 1 известны относительные погрешности δ(x) = 0,001 и δ(y) = 0,002. Относительная погрешность разности δ(x – y) равна
0,004
0,0002
0,003
0,001
Матрица A= 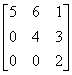 называется
называется
 называется
называетсятреугольной
верхней треугольной
трехдиагональной
ленточной
Верны ли утверждения? Возможны следующие виды матриц: А) продольная В) прямоугольная
A – нет, B – да
A – да, B – да
A – нет, B – нет
A – да, B – нет
Даны линейные системы 1) 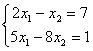 2)
2) 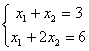 3)
3) 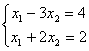 4)
4) 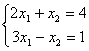 . Свойством диагонального преобладания обладают системы
. Свойством диагонального преобладания обладают системы
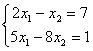 2)
2) 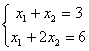 3)
3) 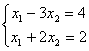 4)
4) 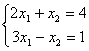 . Свойством диагонального преобладания обладают системы
. Свойством диагонального преобладания обладают системы1 и 4
3 и 4
1 и 2
1, 3 и 4
Для величин x = 2, y = 1, z = 2 заданы их относительные погрешности δ(x)=0,005; δ(y) = 0,001; δ(z) =0,002. Относительная погрешность произведения δ(x ∙ y ∙z) равна
0,0002
0,0000002
0,0001
0,008
Для линейной системы уравнений 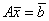 известно LU – разложение матрицы A = LU. Тогда количество систем уравнений с треугольными матрицами, к которым сводится решение исходной системы уравнений, равно
известно LU – разложение матрицы A = LU. Тогда количество систем уравнений с треугольными матрицами, к которым сводится решение исходной системы уравнений, равно
трем
четырем
единице
двум
Для величин x и z заданы их абсолютные погрешности ∆(x) = 0,02; ∆(z) = 0,07 . Тогда абсолютная погрешность величины ∆(x− z) будет равна
0,05
0,01
-0,05
0,09
Степень обусловленности линейной системы уравнений 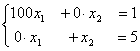 равна
равна
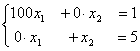 равна
равна10
50
0,01
100
Верны ли утверждения? Возможны следующие виды матриц: А) единичная B) нулевая
A – нет, B – да
A – да, B – да
A – нет, B – нет
A – да, B – нет
Система линейных уравнений называется недоопределенной, если
все коэффициенты системы являются иррациональными числами
не все коэффициенты системы заданы
количество уравнений меньше количества неизвестных
не заданы правые части системы
Для величин x = 5 и y = 1 известны абсолютные погрешности ∆(x) = 0,001 и ∆(y) = 0,0005. Абсолютная погрешность частного ∆(x/y) равна
0,0015
0,0035
0,0005
0,000005
Верны ли утверждения? Возможны следующие виды погрешностей: A) чередующиеся В) относительные
A – нет, B – нет
A – да, B – да
A – нет, B – да
A – да, B – нет
Задана линейная система 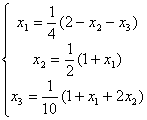 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен
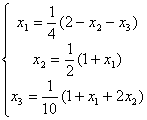 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен{0,5; 1,2; 0,1}
{0,5; 0,5; 0,1}
{0,5; 0,75; 0,3}
{0,75; 1,2; 0,1}
Задана линейная система уравнений с симметричной матрицей 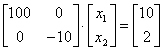 . Ее степень обусловленности равна
. Ее степень обусловленности равна
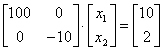 . Ее степень обусловленности равна
. Ее степень обусловленности равна5
1000
10
-10
Система линейных уравнений называется определенной, если
коэффициенты системы являются рациональными
правые части заданы с высокой точеностью
коэффициенты системы являются целыми числами
количество уравнений равно количеству неизвестных
Алгоритм называется неустойчивым, если
малые изменения исходных данных и погрешности округления приводят к значительному изменению окончательных результатов
большие изменения в исходных данных приводят к малому изменению результата
большие изменения в исходных данных не изменяют окончательный результат
малые изменения исходных данных не изменяют окончательный результат
Задана линейная система 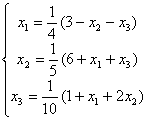 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен
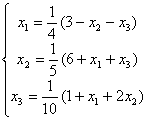 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0, один шаг метода Зейделя {x1(1), x2(1), x3(1)} будет равен{0,75; 1,35; 0,445}
{0,75; 1,2; 0,1}
{0,75; 1,2; 0,445}
{0,75; 1,35; 0,05}
Верны ли утверждения? В методе Гаусса решения систем линейных уравнений используются следующие виды матриц: А) верхняя треугольная В) симметричная
A – да, B – да
A – нет, B – нет
A – да, B – нет
A – нет, B – да
Для системы линейных уравнений 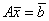 известны обратная матрица A-1 и вектор правых частей
известны обратная матрица A-1 и вектор правых частей 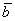 . A-1 =
. A-1 = 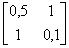 ,
, 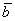 =
= 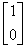 . Тогда вектор решения системы
. Тогда вектор решения системы 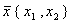 равен
равен
{1,5; 1,1}
{1; 0,1}
{0,5; 1}
{1; 0,5}
Заданы матрицы 1) 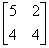 , 2)
, 2) 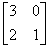 , 3)
, 3) 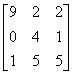 . Условиям диагонального преобладания удовлетворяют матрицы
. Условиям диагонального преобладания удовлетворяют матрицы
 . Условиям диагонального преобладания удовлетворяют матрицы
. Условиям диагонального преобладания удовлетворяют матрицы1 и 3
1
только 2
2 и 3
Метод Зейделя для системы линейных уравнений 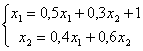
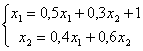
приведет к зацикливанию
сходится при любом начальном приближении
расходится при любом начальном приближении
сходится только при x1 = 0, x2 = 0
Для величин x и z заданы их абсолютные погрешности ∆(x) = 0,05; ∆(z) = 0,02 . Тогда абсолютная погрешность величины ∆(x− z) будет равна
0,07
0,0099
0,01
0,03
Абсолютные погрешности величин x и y равны ∆x = 0,4 и ∆y =0,3. Абсолютная погрешность разности ∆(x – y) равна
1,3333333
0,1
0,7
0,12
Задана линейная система 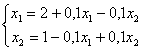 . Первое приближение метода простой итерации
. Первое приближение метода простой итерации 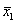 при начальном значении
при начальном значении 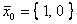 дает результат
дает результат
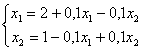 . Первое приближение метода простой итерации
. Первое приближение метода простой итерации {2,1; 0,9}
{2,1; 1,1}
{2; 1}
{2,2; 1,1}
Заданы матрицы 1) 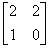 , 2)
, 2) 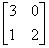 , 3)
, 3) 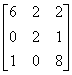 . Условиям диагонального преобладания удовлетворяют матрицы
. Условиям диагонального преобладания удовлетворяют матрицы
 . Условиям диагонального преобладания удовлетворяют матрицы
. Условиям диагонального преобладания удовлетворяют матрицы2 и 3
1
только 2
только 3
Для величин x = 1 и y = 2 известны абсолютные погрешности ∆(x) = 0,001 и ∆(y) = 0,005. Абсолютная погрешность произведения ∆(x∙y) равна
0,007
0,011
0,006
0,000005
Верны ли утверждения? Возможны следующие типы матриц: А) ленточная В) нижняя треугольная
A – нет, B – нет
A – да, B – да
A – да, B – нет
A – нет, B – да
Задана линейная система уравнений в матричном виде 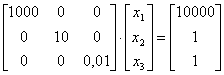 . Ее степень обусловленности равна
. Ее степень обусловленности равна
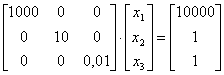 . Ее степень обусловленности равна
. Ее степень обусловленности равна105
0,01
10
104
Сходимость итерационного метода решения систем линейных уравнений зависит от
начального приближения системы
вида матрицы системы
количества нулей в матрице
величины правых частей системы
Дана система уравнений 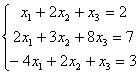 . Для сходимости итерационного метода ее надо записать в виде
. Для сходимости итерационного метода ее надо записать в виде
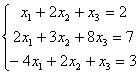 . Для сходимости итерационного метода ее надо записать в виде
. Для сходимости итерационного метода ее надо записать в виде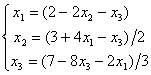
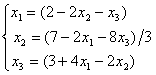
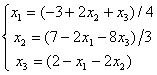
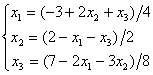
Задана линейная система 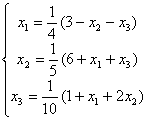 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 один шаг метода простой итерации{x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 один шаг метода простой итерации{x1(1), x2(1), x3(1)} будет равен
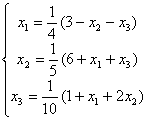 . Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 один шаг метода простой итерации{x1(1), x2(1), x3(1)} будет равен
. Начиная с начального значения x1(0) = x2(0) = x3(0) = 0 один шаг метода простой итерации{x1(1), x2(1), x3(1)} будет равен{0,75; 1,2; 0,1}
{0,75; 1,55; 0,1}
{0,75; 1,55; 4,85}
{0,75; 1,2; 0,5}
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: А) метод 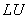 разложения является итерационным методом B) метод Гаусса является прямым методом
разложения является итерационным методом B) метод Гаусса является прямым методом
A – нет, B – да
A – нет, B – нет
A – да, B – да
A – да, B – нет
Параметр релаксации ω для метода верхней релаксации при решении системы линейных уравнений методом итераций лежит в пределах
1 < ω < 2
0 < ω < 1
−1 < ω < 0
2 < ω < 3
Для обратного хода метода Гаусса подготовлены следующие системы уравнений 1) 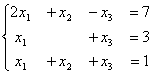 2)
2) 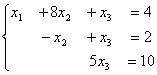 3)
3) 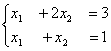
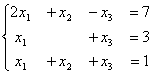 2)
2) 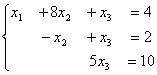 3)
3) 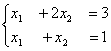
только 2
2 и 3
3
1 и 2
Линейная система уравнений задана в виде 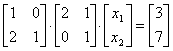 . Тогда x1 и x2 равны
. Тогда x1 и x2 равны
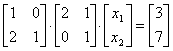 . Тогда x1 и x2 равны
. Тогда x1 и x2 равны{1; 2}
{2; 1}
{1; 1}
{2; 0}
Достаточные условия сходимости метода Зейделя для системы линейных уравнений с матрицей A заключаются в том, что
aii ≠ 0 ( i = 1, 2, . . . n)
Верны ли утверждения? Даны линейные системы 1)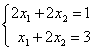 2)
2)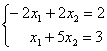 3)
3)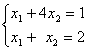 4)
4)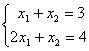 . Свойством диагонального преобладания обладают системы А) только 3 В) 2 и 4
. Свойством диагонального преобладания обладают системы А) только 3 В) 2 и 4
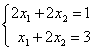 2)
2)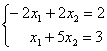 3)
3)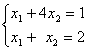 4)
4)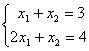 . Свойством диагонального преобладания обладают системы А) только 3 В) 2 и 4
. Свойством диагонального преобладания обладают системы А) только 3 В) 2 и 4A – да, B – нет
A – нет, B – нет
A – да, B – да
A – нет, B – да
Верны ли утверждения? При математическом моделировании на компьютере для возникающих погрешностей справедливы следующие утверждения: А) Погрешность математической модели является неустранимой В) Погрешность численного метода является регулируемой
A – да, B – нет
A – да, B – да
A – нет, B – да
A – нет, B – нет
Для величин x, y и z заданы их абсолютные погрешности ∆(x) = 0,008; ∆(y) = 0,004 ; ∆(z) = 0,001. Тогда абсолютная погрешность величины ∆(x+y− z) будет равна
0,013
0,008
0,001
0,011
Верны ли утверждения? Заданы системы линейных уравнений 1) 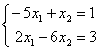 2)
2) 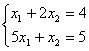 3)
3) 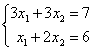 . Свойством диагонального преобладания обладают матрицы систем: А) 1 и 3 B) только 2
. Свойством диагонального преобладания обладают матрицы систем: А) 1 и 3 B) только 2
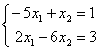 2)
2) 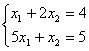 3)
3) 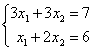 . Свойством диагонального преобладания обладают матрицы систем: А) 1 и 3 B) только 2
. Свойством диагонального преобладания обладают матрицы систем: А) 1 и 3 B) только 2A – да, B – нет
A – нет, B – да
A – да, B – да
A – нет, B – нет
Верны ли утверждения? Метод Зейделя для системы линейных уравнений 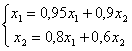 А) сходится при любом начальном приближении В) приведет к зацикливанию
А) сходится при любом начальном приближении В) приведет к зацикливанию
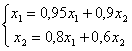 А) сходится при любом начальном приближении В) приведет к зацикливанию
А) сходится при любом начальном приближении В) приведет к зацикливаниюA – нет, B – нет
A – да, B – нет
A – нет, B – да
A – да, B – да
Выбор начального приближения на сходимость метода Зейделя при решении систем линейных уравнений
влияет, если матрица не симметричная
влияет, если матрица не является верхней треугольной
не влияет, если матрица является ленточной
не влияет
Дана система 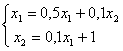 , задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение
, задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение
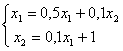 , задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение
, задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение(0,6; 1,1)
(0,1; 1,06)
(0,6; 1)
(0,6; 1,06)
Число 0,0037 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление
37
Заданы матрицы 1) 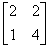 , 2)
, 2) 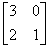 , 3)
, 3) 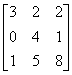 . Условиям диагонального преобладания удовлетворяют матрицы
. Условиям диагонального преобладания удовлетворяют матрицы
 . Условиям диагонального преобладания удовлетворяют матрицы
. Условиям диагонального преобладания удовлетворяют матрицытретья
вторая и третья
первая и вторая
Первая