Математика (курс 7)
Случайная величина Х распределена по нормальному закону, ее математическое ожидание равно нулю, а среднеквадратическое отклонение равно 20. Плотность распределения Х имеет вид
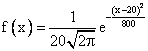
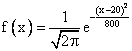
Случайная величина имеет показательное распределение с математическим ожиданием, равным 7. Плотность вероятности такой величины равна
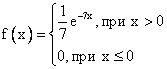
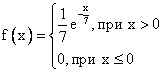
Корректура книги объемом в 500 страниц имеет 500 ошибок. Число опечаток на одной странице - случайная величина, распределенная по закону Пуассона. Вероятность того, что на случайно выбранной странице окажется 2 опечатки, равна
В партии из 10 деталей 8 стандартных. Наугад выбирается две детали. Вероятность того, что они будут стандартными, равна
0,9
0,8
Медиана случайной величины, распределенной нормально, равна 2,5, а ее среднеквадратическое отклонение равно 3. Тогда плотность распределения этой величины имеет вид
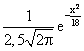
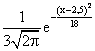
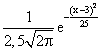
Случайная величина распределена по нормальному закону, ее математическое ожидание равно 1, а дисперсия - 25. Тогда ее функция распределения имеет вид
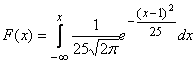
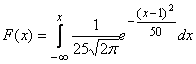


В аквариуме плавают рыбки: 10 меченосцев и 6 вуалехвостов. Наугад ловится одна рыбка. Вероятность того, что это будет меченосец, равна
0,48
0,5
0,9
Квантиль распределения Кр уровня Р непрерывной случайной величины с функцией распределения F(x) определяется как решение уравнения
Вероятность события может быть равна
любому числу из отрезка [0,1]
любому числу
любому числу отрезка [-1,1]
любому положительному числу
Для математического ожидания произведения случайной величины Х и постоянной С справедливо свойство:
М(СХ) = |C| МХ
М(СХ) = 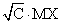
М(СХ) = C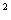 МХ
МХ
М(СХ) = С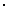 МХ
МХ
Вероятность того, что студент сдаст экзамен по математике, равна 0,5, а экзамен по иностранному языку - 0,6. Вероятность того, что он сдаст хотя бы один экзамен, равна
Три шарика случайным образом помещают в трех ящиках. Вероятность того, что в каждом ящике окажется по одному шарику, равна
Случайная величина Х распределена по нормальному закону, ее плотность вероятности 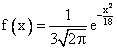 . Тогда ее МХ, DX и
. Тогда ее МХ, DX и 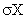 таковы:
таковы:
0; 9; 3
3; 0; 9
3; 3; 9
0; 3; 9
Математическое ожидание непрерывной случайной величины - это
Случайная величина Х имеет распределение Пуассона с параметром 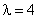 . Ее числовые характеристики равны
. Ее числовые характеристики равны
Случайная величина имеет показательное распределение с плотностью 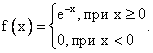 Тогда функция распределения равна
Тогда функция распределения равна
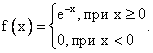 Тогда функция распределения равна
Тогда функция распределения равна
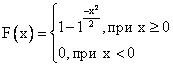
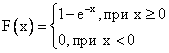
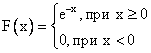
Случайная величина Х распределена равномерно на 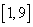 , тогда вероятность попасть в интервал
, тогда вероятность попасть в интервал 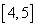 равна
равна
Случайная величина Х имеет распределение Пуассона с параметром 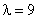 . Ее числовые характеристики равны
. Ее числовые характеристики равны
Если известна вероятность события А, равная Р(А), то вероятность противоположного события Р(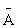 ) определяется как
) определяется как
1 - 2 Р(А)
1 - Р(А)
2 Р(А)
Вероятность суммы двух случайных событий вычисляется по формуле
Р(А+В) = Р(А) + Р(В) - Р(АВ)
Р(А+В) = Р(А)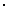 Р(В)
Р(В)
Р(А+В) = Р(А) + Р(В)
Р(А+В) = Р(А) + Р(В/А)
Случайная величина Х имеет нормальное распределение с плотностью распределения 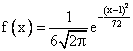 . Тогда ее числовые характеристики МХ, DX и
. Тогда ее числовые характеристики МХ, DX и 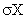 равны соответственно
равны соответственно
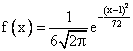 . Тогда ее числовые характеристики МХ, DX и
. Тогда ее числовые характеристики МХ, DX и 1; 36; 6
1; 6; 36
6; 1; 1
36; 1: 6
Случайная величина Х имеет биномиальное распределение с параметрами 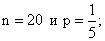 тогда ее числовые характеристики таковы:
тогда ее числовые характеристики таковы:
Дисперсия произведения случайной величины Х и постоянной С равна
D(CX) = 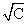 DX
DX
D(CX) = C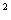 DX
DX
D(CX) = |C| DX
D(CX) = C DX
DX
Если события А, В, С независимы, то
Р(А+ В+С) = Р(А) 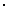 Р(В)
Р(В) 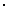 Р(С)
Р(С)
Р(А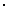 В
В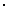 С) = Р(А) + Р(В) + Р(С)
С) = Р(А) + Р(В) + Р(С)
Р(А + В + С) = Р(А) + Р(В) + Р(С)
Р(А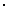 В
В С) = Р(А)
С) = Р(А) Р(В)
Р(В)  Р(С)
Р(С)
Среднеквадратическое отклонение суммы случайной величины Х и постоянной С равно:
Случайная величина Х распределена по нормальному закону. Известно, что математическое ожидание и среднеквадратическое отклонение этой случайной величины соответственно равны 30 и 10. Плотность распределения Х имеет вид
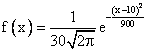
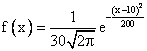
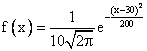
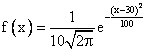
Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле
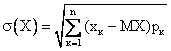
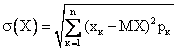
Дискретная случайная величина Х имеет биномиальное распределение с параметрами 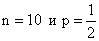 , тогда ее мода и математическое ожидание равны соответственно
, тогда ее мода и математическое ожидание равны соответственно
10; 5
5; 25
5; 5
10;25
Случайная величина, распределенная по нормальному закону, имеет математическое ожидание, равное 5, и среднеквадратическое отклонение, равное 15. Тогда ее функция распределения имеет вид
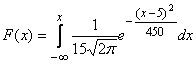


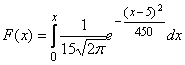
Случайная величина Х называется нормированной, если
МХ = 0; DX =1
МХ = 1; DX =МХ
МХ = 1; DX 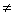 0
0
МХ = 0; DX = М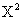
В течение часа коммутатор получает в среднем 30 вызовов. Вероятность того, что на коммутатор не поступит ни одного вызова в течение часа, равна
В урне находятся 5 белых, 4 зеленых и 3 красных шара. Наугад извлекается один шар. Вероятность того, что он будет цветным, равна
0,5
1
На ткацком станке нить обрывается в среднем 0,3 раза в течение часа работы станка. Вероятность того, что нить оборвется трижды за час, равна
Случайная величина Х имеет биномиальное распределение с параметрами 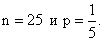 Ее числовые характеристики таковы:
Ее числовые характеристики таковы:
Случайная величина Х распределена нормально с плотностью 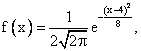 ее мода и медиана равны соответственно
ее мода и медиана равны соответственно
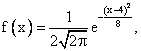 ее мода и медиана равны соответственно
ее мода и медиана равны соответственно4; 2
2; 4
2; 2
4; 4
Вероятность события А равна Р(А) = 0,3; вероятность В равна Р(В) =0,2. Известно, что события А и В независимы. Тогда вероятность произведения 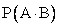 равна
равна
0,06
0,5
0,32
0,23
Вероятность безотказной работы каждой из 5 однотипных машин в течение заданного времени равна 0,8. Вероятность того, что по истечении заданного времени безотказно проработают две машины, а откажут три, равна
Баскетболист попадает в корзину мячом с вероятностью 0,7. Вероятность попасть мячом в корзину из пяти бросков три раза равна
В физкультурной группе 11 спортсменов и среди них 6 перворазрядников. Вероятность того, что среди 2 случайно выбранных спортсменов окажется два перворазрядника, равна
0,11
Вероятность перегорания лампы в течение некоторого времени рана 0,02. Вероятность того, что за это время перегорит только одна из восьми ламп, равна
Функция распределения непрерывной случайной величины
ступенчатая
непрерывна
скачкообразная
кусочно-непрерывна
Случайная величина имеет показательное распределение с параметром 2. Тогда ее плотность распределения
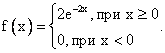
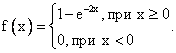
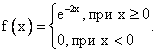
Среднеквадратическое отклонение непрерывной случайной величины вычисляется по формуле
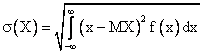
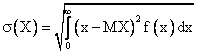
На тестировании студент выбирает наугад один ответ из 4 возможных, среди которых один ответ верный. Вероятность того, что он правильно ответит хотя бы на один вопрос из двух предложенных тестов, равна