Уравнения математической физики (курс 2)
Уравнение теплопроводности после преобразования Фурье имеет вид
s2u - uxx = 0
ut + s2u = 0
s2u + uxx = 0
ut - s2u = 0
Задача ______ для уравнения теплопроводности - задача об отыскании решения уравнения теплопроводности, удовлетворяющего начальному условию – распределению температуры
Решением уравнения Uxx - Uyy = 0 является функция
U = 2x + 2y2
U = x2 + 2y
U = x2 – y2
U = (x – y)2
Выражение вида f(x) =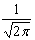
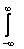F(s)eixsds называется _____ Фурье
F(s)eixsds называется _____ Фурьеобратным преобразованием
разложением
интегралом
коэффициентом
Дополнительные условия, которым должно удовлетворять решение нестационарного уравнения в начальный момент времени, называются
неоднородными
начальными
конечными
однородными
Если функция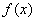 
определена для всех 
, то ей соответствует 
, которая для является ___ Фурье
определена для всех 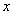, то ей соответствует 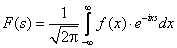, которая для 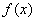является ___ ФурьеВерны ли утверждения? А) Фронт волны – это граница между возмущённой и невозмущенной областями среды В) Свёртка функций представляет собой интегральное преобразование двух функци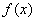й и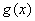 
, задаваемое формулой 
Подберите правильный ответ
и , задаваемое формулой 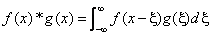Подберите правильный ответА – нет, В - нет
А – да, В - нет
А – да, В - да
А – нет, В - да
Ортогональные функции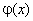 
и 
- это
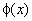и - этофункции, определённые в интервале,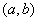 
и такие, что 
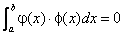, но 
и 
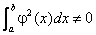и такие, что , но и 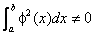однозначные функции, аналитические в каждой точке интервала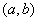
функции, определённые и не равные 0 в интервале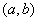
Преобразование Фурье F[f] по х функции f(x,t) имеет свойство
F[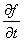
] = 
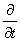F[f]
] = F[f]F[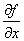
] = 
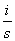F[f]
] = F[f]F[] = is F[f]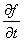
] = is F[f]F[] =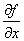 
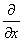F[f]
] = F[f]Переставьте строки в правом столбце так, чтобы строки в обоих столбцах соответствовали друг другу
среднее значение функции, заданной на поверхности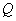 
среднее значение функции, заданной на плоской кривой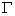 
среднее значение функции, заданной в области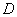 
Переставьте строки в правом столбце так, чтобы строки в обоих столбцах соответствовали друг другу
уравнение гиперболического типа в области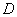
уравнение, которое имеет разный тип в разных точках области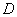
уравнение эллиптического типа в области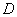
уравнение, имеющее в каждой точке области 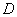параболический тип
параболический типуравнение параболического типа в области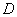
уравнение, имеющее в каждой точке области 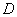эллиптический тип
эллиптический типуравнение смешанного типа в области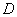
уравнение, имеющее в каждой точке области 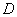гиперболический тип
гиперболический типЕсли функция 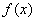определена для всех , то ей соответствует , которая для является ___ Фурье
определена для всех 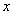, то ей соответствует 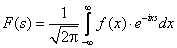, которая для 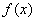является ___ Фурьеобратным преобразованием
преобразованием
ядром обратного преобразования
ядром преобразования
Ортогональная система функций - это
последовательность функций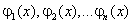 
, попарно ортогональных в интервале
, попарно ортогональных в интервале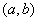 функции, определённые и не равные 0 в интервале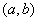
функции, непрерывные в каждой точке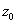 
интервала
интервала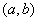 однозначные функции, аналитические в каждой точке интервала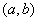
Уравнение Лапласа на плоскости имеет вид
Uxx + Uyy = 0
Ux = Uyy
Uxx = Uyy + Uzz
Uxx = Uyy
Верны ли утверждения? А) Уравнение z2(Uxx)2 + x2(Uyy)2 - y2(Uzz)2 = 0 линейное второго порядка В) Уравнение Uxx + x2Uy + zU = 0 линейное второго порядка Подберите правильный ответ
А – да, В – нет
А – нет, В – нет
А – нет, В – да
А – да, В – да
Верны ли утверждения? А) При решении задачи Коши для уравнения теплопроводности можно использовать метод Фурье В) При решении волнового уравнения можно использовать метод характеристик Подберите правильный ответ
А – нет, В - нет
А – да, В - да
А – да, В - нет
А – нет, В - да
Решением уравнения Uxy = 0 является функция
U = x2 + y2
U = xy
U = x2y2
U = (x –1)(y + 1)
Сопоставьте термины и их определения
Задача Коши для уравнения теплопроводности
найти значения параметраl,при которых уравнение [p(x)y¢]¢-q(x)y+lr(x)y=0,0<>
Задача Неймана (вторая краевая задача) для уравнения Лапласа (Пуассона)
задача об отыскании решения уравнения Лапласа (или уравнения Пуассона), удовлетворяющего условию Неймана на границе области
Задача Штурма-Лиувилля
задача об отыскании решения уравнения теплопроводности, удовлетворяющего начальному условию – распределению температуры
Установить соответствие между волновым уравнением и размерностью пространства, для которого оно записано
3 -мерное пространство
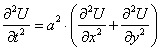
двумерное (плоскость)
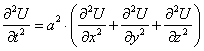
одномерное (прямая)
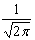
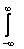Выражение вида F(s) =f(x)e-ixsdx называется
f(x)e-ixsdx называетсякоэффициентом Фурье
преобразованием Фурье функции f(x)
интегралом Фурье
разложением Фурье
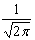
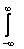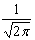
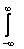Преобразования Фурье f(x) =F(s)eixsds и F(s) =f(x)e-ixsdx называются
F(s)eixsds и F(s) =f(x)e-ixsdx называютсявзаимно обратными
обратно сопряжёнными
взаимно противоположными
взаимно сопряжёнными
Переставьте строки в правом столбце так, чтобы строки в обоих столбцах соответствовали друг другу
принцип максимума для гармонической функции
гармоническая на всей плоскости функция не может быть ограниченной сверху или снизу, если она не постоянная
гармоническая функция
значение гармонической функции в некоторой точке плоскости равно среднему значению этой функции на окружности с центром в этой точке
теорема о среднем для гармонических функций
решение уравнения Лапласа, имеющее непрерывные частные производные второго порядка
теорема Лиувилля
всякая гармоническая функция, отличная от постоянной и непрерывная вплоть до границы области, не может принимать своего максимального (минимального) значения во внутренней точке области
Дифференциальное уравнение в точке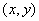 
имеет вид 
. Если его дискриминант 
, оно называется уравнением __ типа
имеет вид 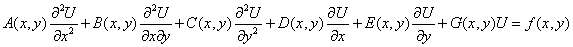. Если его дискриминант 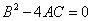, оно называется уравнением __ типаРешением уравнения Uxx + Uyy = 0 является функция
U = x2y
U = x + y2
U = x2 – y2
U = x2 + y2
Дифференциальное уравнение в точке 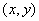имеет вид . Если его дискриминант 
, называется уравнением __ типа
имеет вид 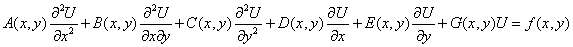. Если его дискриминант 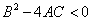, называется уравнением __ типаГраничные условия первого, второго или третьего рода, в которых правая часть тождественно равна нулю
Начальные граничные условия
Дифференциальные граничные условия
Однородные граничные условия
Неоднородные граничные условия
Преобразование Фурье F[f] по х функции f(x,t) имеет свойство
F[ft] = 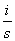F[f]
F[f]F[] = is F[f]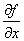
] = is F[f]F[ft] = is F[f]
F[fх] = 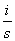F[f]
F[f]Установите соответствие между записью оператора Лапласа в различных координатах
в цилиндрических координатах
в полярных координатах (на плоскости)
в декартовых координатах
Установите соответствие между строками в правом и левом столбцах
обратное преобразование Фурье функции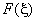 
преобразование Фурье функции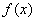
ядро преобразования Фурье
Верны ли утверждения? А) Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Б) Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно независимые.
А - нет, Б - да
А – да, Б - да
А - да, Б - нет
А - нет, Б - нет
Дополнительные условия, которым должно удовлетворять решение дифференциального уравнения на границе области (в частности, на концах интервала (а, b)) – это
начальные условия
граничные условия
конечные условия
дифференциальные условия
у¢(а) = у¢(b) = 0 – это краевые условия ______________ рода задачи Штурма-Лиувилля
третьего
первого
четвертого
второго
Установить соответствие между строками в правом и левом столбцах
обратное интегральное преобразование
преобразование функций, которое каждой функции 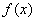ставит в соответствие новую функцию 
ставит в соответствие новую функцию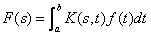 пара интегральных преобразований
функция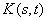 
в интегральном преобразовании
в интегральном преобразованииядро преобразования
прямое и обратное интегральные преобразования
интегральное преобразование
восстанавливает первоначальную функцию из преобразованной
Волна, возникающая в случае, когда начальное отклонение отсутствует, а начальная скорость отлична от 0, называется волной
Верны ли утверждения? А) Уравнение yUxx + xUyy – z2Uzz = 0 имеет второй порядок В) Уравнение y2Uxy – x2Uzx + z2 Uzy = 0 имеет второй порядок Подберите правильный ответ
А – нет, В – да
А – да, В – да
А – нет, В – нет
А – да, В – нет
Дифференциальное уравнение в точке 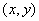имеет вид . Если его дискриминант 
, называется уравнением __ типа
имеет вид 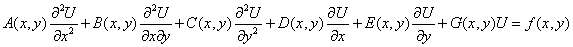. Если его дискриминант 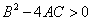, называется уравнением __ типаКоэффициент А(l) в задаче Коши для уравнения теплопроводности Ut = Uxx, U(x,0) = j(x) вычисляется по формуле А(l) =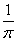 
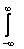j(x)cosx
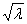dx.Тогда коэффициент А(l) при U(x,0) = j(x) = 
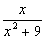равен
j(x)cosxdx.Тогда коэффициент А(l) при U(x,0) = j(x) = равен
1
0
Свёрткой функций f(x) и g(x) называется функция
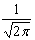
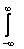f*g =f(x)g(x)dx
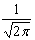
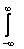f(x)g(x)dxf*g =f(x-x)g(x)dx
f(x-x)g(x)dxf*g =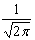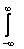f(x)g(x)dx
f(x)g(x)dxf*g =f(x)g(x)dx
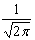
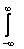f(x)g(x)dxПорядком дифференциального уравнения называется
наивысшая степень переменных, входящих в уравнение
наивысший порядок производных, входящих в уравнение
наивысшая степень производных, входящих в уравнение
наивысшая степень функций, входящих в уравнение
Сопоставьте термины и их определения
Норма функции
тригонометрический ряд Фурье вида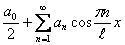 
, где n=1, 2, 3,…, в которм коэффициенты а0, аn вычисляются по формулам 
период Т = 2ℓ
, где n=1, 2, 3,…, в которм коэффициенты а0, аn вычисляются по формулам 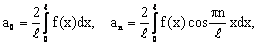период Т = 2ℓОртонормированная система функций на [a,b]
система функций, все функции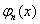 
которой имеют единичную норму и попарно ортогональны на [a, b]
которой имеют единичную норму и попарно ортогональны на [a, b]Ряд Фурье функции 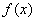по косинусам
по косинусамчисло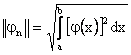 
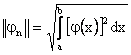
Сопоставьте термины и их определения
Канонический вид уравнений эллиптического типа
уравнение вида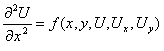 
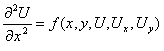
Канонический вид уравнений гиперболического типа
уравнение вида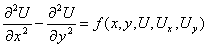 
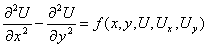
Канонический вид уравнений параболического типа
уравнение вида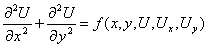 
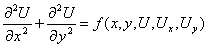
Распределение температуры в физическом теле, не зависящее от времени, называется ___ распределением температуры
Верны ли утверждения? А) Объёмный потенциал выражается как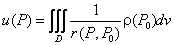 
В) Потенциал простого слоя выражается как 
Подберите правильный ответ
В) Потенциал простого слоя выражается как 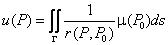Подберите правильный ответА – да, В - да
А – нет, В - нет
А – нет, В - да
А – да, В - нет
Сопоставьте термины и их определения
Собственная функция задачи Штурма-Лиувилля
распределение температуры в физическом теле, не зависящее от времени
Собственное значение задачи Штурма-Лиувилля
значение параметра l, при котором задача Штурма-Лиувилля имеет ненулевое решение
Стационарное распределение температуры
ненулевое решение задачи Штурма-Лиувилля, соответствующее собственному значению
Верны ли утверждения? А) Собственная функция задачи Штурма-Лиувилля - ненулевое решение задачи Штурма-Лиувилля, соответствующее собственному значению λ В) Собственное значение задачи Штурма-Лиувилля - значение параметра l, при котором задача Штурма-Лиувилля имеет ненулевое решение Подберите правильный ответ
А – нет, В - нет
А – нет, В - да
А – да, В - нет
А – да, В - да
Волна, возникающая в случае, когда начальная скорость во всех точках равна 0, а начальное отклонение отлично от 0, называется волной
Задача Коши для уравнения теплопроводности имеет вид
, 
, , 
, 
Дифференциальное уравнение называется линейным, если
все независимые переменные входят в уравнение в первой степени
все неизвестные функции входят в уравнение в первой степени
все неизвестные функции и их производные входят в уравнение в первой степени
все переменные входят в уравнение в первой степени
у(а) = у(b) = 0– это краевые условия ______________ рода задачи Штурма-Лиувилля
первого
третьего
четвертого
второго
Сопоставьте термины и их определения
Уравнение теплопроводности на плоскости
уравнение с частными производными второго порядка вида: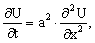 
гдеU-неизвестная функция,а>0-постоянная
гдеU-неизвестная функция,а>0-постояннаяУравнение теплопроводности в пространстве
уравнение с частными производными второго порядка вида: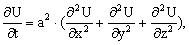 
гдеU-неизвестная функция,а>0-постоянная
гдеU-неизвестная функция,а>0-постояннаяУравнение теплопроводности (одномерное)
уравнение с частными производными второго порядка вида: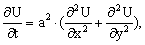 
гдеU-неизвестная функция,а>0-постоянная
гдеU-неизвестная функция,а>0-постоянная