Математика (курс 11)
Пусть исследуемая величина 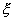 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 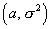 и по выборке вычисляется выборочная дисперсия
и по выборке вычисляется выборочная дисперсия 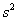 . Тогда имеет распределение
. Тогда имеет распределение 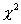 с
с 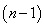 степенями свободы
степенями свободы
величина 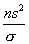
величина 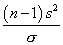
величина 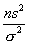
величина 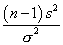
Дисперсия случайной величины 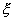 , равной общему числу успехов в
, равной общему числу успехов в 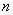 испытаниях Бернулли с вероятностью успеха в одном испытании, равной
испытаниях Бернулли с вероятностью успеха в одном испытании, равной 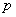 , равна
, равна
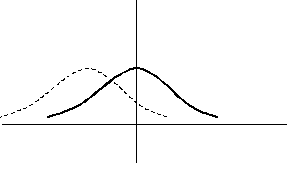
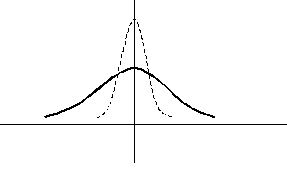
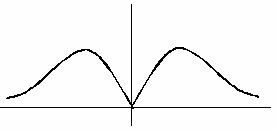
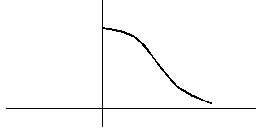
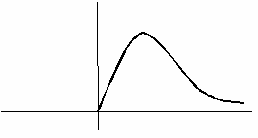
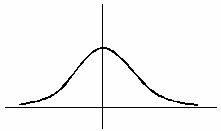
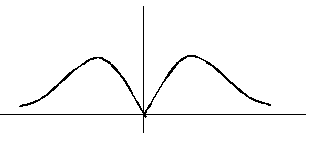
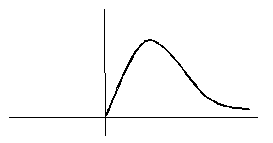
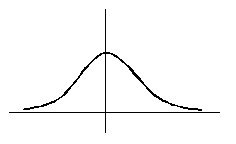
На рисунке сплошной линией изображен график плотности стандартного нормального распределения. График плотности нормального распределения с параметрами 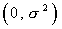 ,
, 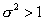 , изображенный пунктиром, имеет следующий вид
, изображенный пунктиром, имеет следующий вид
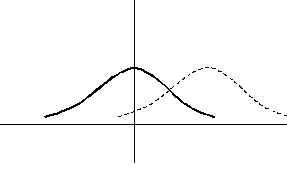
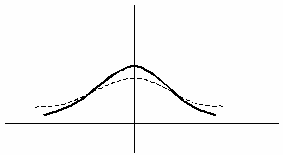
Пусть исследуемая случайная величина 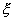 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 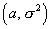 и по выборке вычисляется выборочное среднее
и по выборке вычисляется выборочное среднее 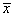 . Тогда имеет нормальное распределение с параметрами (0, 1)
. Тогда имеет нормальное распределение с параметрами (0, 1)
величина 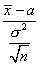
величина 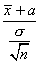
величина 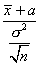
величина 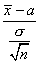
Если выборка задана в виде группированного статистического ряда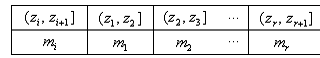 и
и 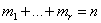 , то выборочное среднее равно
, то выборочное среднее равно
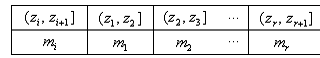 и
и Задача математической статистики -
по известным распределениям одних случайных величин определить распределения других случайных величин
по известным распределениям случайных величин предсказать результаты измерений или наблюдений
по известным распределениям случайных величин определить вероятность различных событий
по результатам измерения или наблюдений сделать выводы о характере распределения исследуемых случайных величин
Случайная величина 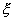 имеет плотность распределения
имеет плотность распределения 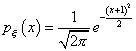 . Ее математическое ожидание равно
. Ее математическое ожидание равно
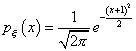 . Ее математическое ожидание равно
. Ее математическое ожидание равно1
2
2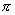
-1
Гистограмма - это наглядное изображение группированного статистического ряда в виде столбчатой диаграммы, состоящей из прямоугольников, у которых
в виде столбчатой диаграммы, состоящей из прямоугольников, у которых
 в виде столбчатой диаграммы, состоящей из прямоугольников, у которых
в виде столбчатой диаграммы, состоящей из прямоугольников, у которыхоснования равны 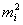 , а площади пропорциональны длинам полуинтервалов
, а площади пропорциональны длинам полуинтервалов 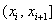
основания равны 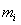 , а площади пропорциональны длинам полуинтервалов
, а площади пропорциональны длинам полуинтервалов 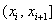
основаниями являются полуинтервалы 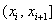 , а площади пропорциональны
, а площади пропорциональны 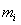
основаниями являются полуинтервалы 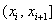 , а площади пропорциональны
, а площади пропорциональны 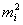
Складываются 300 независимых случайных величин, равномерно распределенных на отрезке [0, 2]. Вероятность того, что их сумма заключена между 280 и 320, примерно равна
Пусть 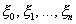 - независимые случайные величины, имеющие нормальное распределение с параметрами (0, 1). Распределение Стьюдента с
- независимые случайные величины, имеющие нормальное распределение с параметрами (0, 1). Распределение Стьюдента с 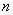 степенями свободы - это распределение случайной величины
степенями свободы - это распределение случайной величины
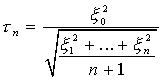
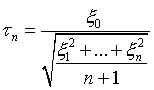
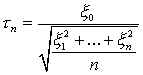
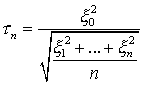
Случайная выборка объема 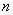 - это полученные в результате
- это полученные в результате 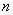 независимых измерений или наблюдений, проведенных в одинаковых условиях,
независимых измерений или наблюдений, проведенных в одинаковых условиях, 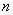 чисел
чисел 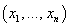 , которые мы считаем
, которые мы считаем
значениями 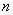 случайных величин
случайных величин 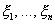 с неизвестными нам распределениями
с неизвестными нам распределениями
значениями случайной величины 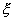 с неизвестным нам распределением
с неизвестным нам распределением
вероятностями различных событий, связанных со случайной величиной 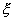
вероятностями событий, связанных с 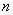 случайными величинами
случайными величинами 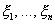
Пусть значение параметра 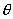 неизвестно. Доверительный интервал, соответствующий доверительной вероятности
неизвестно. Доверительный интервал, соответствующий доверительной вероятности 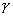 , - это интервал
, - это интервал 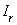 , для которого
, для которого
Математическое ожидание случайной величины, имеющей нормальное распределение с параметрами 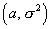 , равно
, равно
К. Пирсон предложил в качестве меры отклонения частот, подсчитанных по выборке, от теоретических вероятностей использовать величину
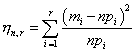
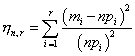
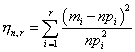
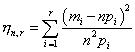
Вариационным рядом называются элементы выборки, расположенные в порядке
возрастания
убывания
произвольном
появления
Пусть при каждом 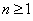 независимые одинаково распределенные случайные величины
независимые одинаково распределенные случайные величины 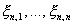 таковы, что
таковы, что 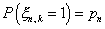 ;
; 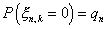 ;
; 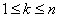 , где
, где 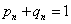 и
и 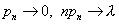 при
при 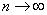 . Положим
. Положим 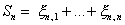 . Тогда при
. Тогда при 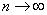
Точность интервальной оценки определяется
значением точечной оценки 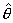
центром доверительного интервала
длиной доверительного интервала
доверительной вероятностью
Проводятся 10 испытаний Бернулли с вероятностью успеха в одном испытании, равной 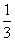 . Наивероятнейшее число наступлений успехов равно
. Наивероятнейшее число наступлений успехов равно
3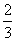
3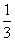
4
3
Если 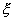 - произвольная случайная величина, то для любого
- произвольная случайная величина, то для любого 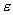 > 0 имеет место неравенство
> 0 имеет место неравенство
Если выборка объема 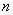 содержит
содержит 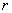 различных элементов
различных элементов 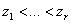 , причем элемент
, причем элемент 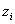 встречается
встречается 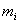 раз, то частота элемента
раз, то частота элемента 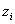 равна
равна
Пусть 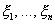 - независимые случайные величины, имеющие нормальное распределение с параметрами (0, 1). Распределение
- независимые случайные величины, имеющие нормальное распределение с параметрами (0, 1). Распределение 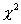 (хи-квадрат) с
(хи-квадрат) с 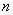 степенями свободы - это распределение случайной величины
степенями свободы - это распределение случайной величины
Пусть исследуемая случайная величина распределена нормально. Доверительный интервал для параметра 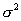 при неизвестном
при неизвестном 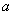 имеет вид
имеет вид
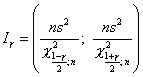
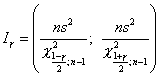
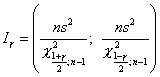
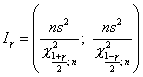
Пусть 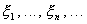 - последовательность независимых одинаково распределенных случайных величин, причем
- последовательность независимых одинаково распределенных случайных величин, причем 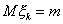 ,
, 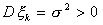 . Положим
. Положим 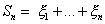 . Тогда для любого
. Тогда для любого 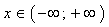 при
при 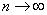 имеет место сходимость
имеет место сходимость
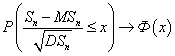
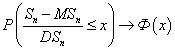
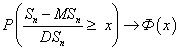
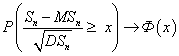
«Законом редких событий» называют распределение
Нормальное
Равномерное
Пуассона
Показательное
Пусть 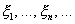 - последовательность независимых одинаково распределенных случайных величин, причем
- последовательность независимых одинаково распределенных случайных величин, причем 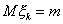 ,
, 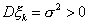 . Положим
. Положим 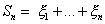 . При больших
. При больших 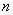 вероятность
вероятность 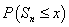 примерно равна
примерно равна
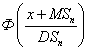
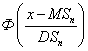
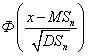
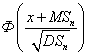
Случайная величина, имеющая нормальное распределение с параметрами 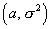 , - это случайная величина
, - это случайная величина 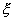 , плотность распределения которой равна
, плотность распределения которой равна
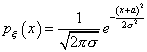
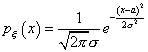
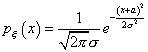
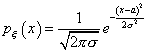
Игральная кость подбрасывается шесть раз. Вероятность того, что пять раз выпадет три очка, равна
Математическое ожидание случайной величины 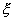 , равной общему числу успехов в
, равной общему числу успехов в 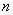 испытаниях Бернулли с вероятностью успеха в одном испытании, равной
испытаниях Бернулли с вероятностью успеха в одном испытании, равной 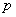 , равно
, равно
(np)2
Дисперсия случайной величины 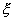 , имеющей распределение Пуассона с параметром
, имеющей распределение Пуассона с параметром 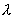 , равна
, равна
2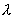
Правильная монета подбрасывается 400 раз. Вероятность того, что выпавших гербов будет от 170 до 220, примерно равна
Вероятность попадания в интервал 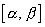 случайной величины, имеющей нормальное распределение с параметрами
случайной величины, имеющей нормальное распределение с параметрами 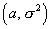 , равна
, равна
Правильная монета подбрасывается 10000 раз. Вероятность того, то частота выпадений герба окажется в интервале [0,49; 0,51], примерно равна
Пусть имеется выборка объема 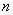 :
: 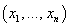 . Если эта выборка содержит
. Если эта выборка содержит 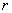 различных элементов
различных элементов 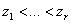 , причем элемент
, причем элемент 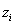 встречается
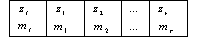
встречается 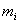 раз, то полученные результаты можно представить в виде статистического ряда, который имеет следующий вид:
раз, то полученные результаты можно представить в виде статистического ряда, который имеет следующий вид:
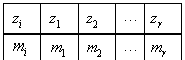
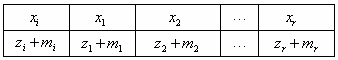

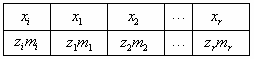
Складываются 100 независимых случайных величин, равномерно распределенных на отрезке [0, 12]. Дисперсия суммы равна
600
1200
14400
2400
Если для потока событий вероятность появления 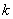 событий в любом промежутке времени не зависит от того, сколько событий и в какие моменты появлялись до этого промежутка, то говорят, что поток событий обладает
событий в любом промежутке времени не зависит от того, сколько событий и в какие моменты появлялись до этого промежутка, то говорят, что поток событий обладает
отсутствием последействия
стационарностью
однородностью
независимостью
Дисперсия случайной величины, имеющей нормальное распределение с параметрами 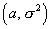 , равна
, равна
Выборка представлена в виде группированного статистического ряда: Объем выборки равен
Объем выборки равен
 Объем выборки равен
Объем выборки равен20
35
5
6
На АТС поступает простейший поток вызовов с интенсивностью один вызов в минуту. Вероятность того, что за две минуты поступит хотя бы один вызов, приближенно равна
Если 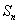 - число успехов в
- число успехов в 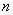 испытаниях Бернулли с вероятностью успеха в одном испытании, равной
испытаниях Бернулли с вероятностью успеха в одном испытании, равной 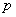 , то при больших
, то при больших 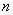
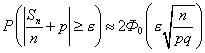
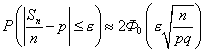
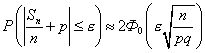
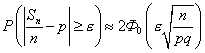
Надежность интервальной оценки определяется
длиной доверительного интервала
значением точечной оценки 
центром доверительного интервала
доверительной вероятностью
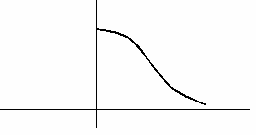
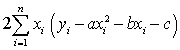
 и
и