Дискретная математика
Вычисление попарных расстояний Хэмминга для кодовых слов алфавита V = {a, b, c} a: 10101, b: 10110, c: 10011 b: 00110, c: 11011, a: 01101 (второй ряд записан под первым для удобства вычислений) показывает, что кодовое расстояние данного кода равно
5
4
3
2
При передаче сообщения 1011001 произошла ошибка вида L ® 1 между 3-м и 4-м разрядами. На приемнике получено сообщение ___________.
Количество различных двухбуквенных комбинаций, которые можно составить из букв, входящих в слово «СТОЛ» (все буквы в комбинации различны), равно
23
4
5
12
Сумма чисел 1111 и 101, записанных в двоичной системе счисления, равна
10010
10101
11100
10100
Стоимость S кода алфавита с заданными частотами букв a: 01 0.5 b: 1010 0.3 c: 110 0.2 равна
2.8
3.2
1.0
3.0
Если кодовое расстояние для двоичных кодов передаваемых сообщений равно 12, то возможно исправление до ____ ошибок замещения.
Функция, получаемая применением оператора примитивной рекурсии 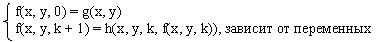
x, y, k
x, y, k, f
x, y
k
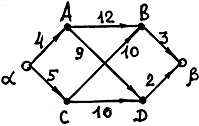
Pасстояние между вершинами А и В в графе с заданными длинами ребер равно 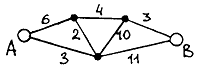

10
12
13
14
Граф переходов представляет машину Тьюринга с ___ состояниями (ответ – целое число). [Замечание: символы, приписываемые вершинам и дугам графа, отсутствуют, поскольку не требуются для решения] 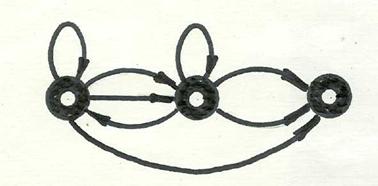

Тезис Тьюринга
декларирует связь интуитивного понятия алгоритма с машинами Тьюринга
устанавливает сводимость машин Тьюринга к рекурсивным функциям
перечисляет основные требования к точному понятию алгоритма
устанавливает сводимость рекурсивных функций к машинам Тьюринга
Рассматривается алфавит, состоящий из букв, входящих в слово «кавардак». С помощью этого алфавита невозможно закодировать слово
ДРАКАР
КАДКА
КАРАВАН
КАКВА
Число сочетаний с повторениями из 5 элементов по 2 вычисляется по формуле
C52
A52
Сумма чисел 1101 и 1011, записанных в двоичной системе счисления, равна
11000
10001
11010
10110
Максимальное число абонентов, которых можно обеспечить 6-значными телефонными номерами, составляет __________ .
Кодовый замок имеет 10 клавиш с цифрами 0, 1, 2,..., 9. Для открывания двери нужно одновременно нажать 4 клавиши. Число всевозможных кодов такого замка равно
А104
С104
Укажите соответствие между комбинаторными числами и их обозначениями:
(n, k)-размещения без повторений
Pn
(n, k)-сочетания с повторениями
Перестановки из n элементов
Аnk
Кодовый замок имеет 10 клавиш с цифрами 0, 1, 2,..., 9. Для открывания двери нужно последовательно нажать 4 клавиши. Число всевозможных кодов такого замка равно
С104
А104
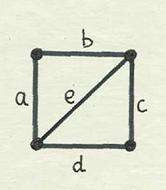
Остов графа образуют ребра 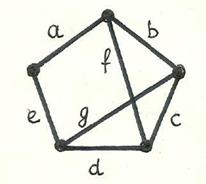

{a, f, c, g}
{a, b, c, d, e}
{a, b, f, d}
{b, c, d, g}
Рассматривается алфавит, состоящий из букв, входящих в слово «тризна». С помощью этого алфавита невозможно закодировать слово
ТИНА
ТРИНЗ
ЗИМА
РАНА
Матрица переходов автомата с входным алфавитом {a, b}, выходным алфавитом {a, b, d} и 10 состояниями имеет размерность
10х10
2х10
10х2
10х3
Количество различных трехбуквенных комбинаций, которые можно составить из букв, входящих в слово «ОКНО» (все буквы в комбинации различны), равно
11
24
2
6
Дерево 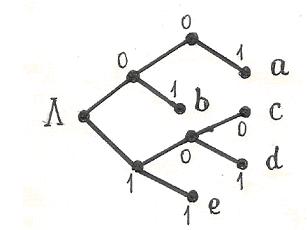 представляет код алфавита
представляет код алфавита
 представляет код алфавита
представляет код алфавитаa: 001, b: 01, c: 100, d: 101, e:11
a: 100, b: 10, c: 001, d: 101, e:11
a: 001, b: 011, c: 101, d: 110, e:111
a: 100, b: 01, c: 101, d: 110, e: 11
Количество различных трехзначных чисел, которые можно составить из цифр 1, 3, 5, 7, 8 (все цифры в числе разные), равно
8
75
14
60
Число переменных функции, получаемой применением оператора примитивной рекурсии 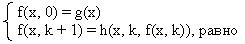
0
1
3
2
Число различных 4-значных четных чисел, которые можно составить из всех цифр числа 4762, равно
6
18
24
12
Если кодовое расстояние для двоичных кодов передаваемых сообщений равно 7, то возможно обнаружение до ____ ошибок замещения.
Количество различных двухбуквенных комбинаций, которые можно составить из букв, входящих в слово «КОМАР» (все буквы в комбинации различны), равно
32
7
20
10
Матрица переходов автомата с входным алфавитом {a, b, c, d}, выходным алфавитом {d, е} и 7 состояниями имеет размерность
7х2
7х4
2х4
4х7
Дана реализация графа: 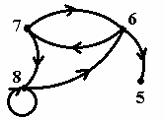 Тогда соответствующим ей множеством вершин (V) и списком дуг (Е) является…
Тогда соответствующим ей множеством вершин (V) и списком дуг (Е) является…
 Тогда соответствующим ей множеством вершин (V) и списком дуг (Е) является…
Тогда соответствующим ей множеством вершин (V) и списком дуг (Е) является…V={5,6,7,8}; Е={(7;6),(6;5),(6;7),(8;7),(8;6)}
V={5,6,7,8}; Е={(7;6),(6;7),(8;7),(6;8),(8;8),(5;6)}
V={5,6,7,8}; Е={(7;6),(6;7),(5;6),(8;8),(8;7)}
V={6,5,7,8}; Е={(7;8),(7;6),(6;7),(8;8),(8;6),(6;5)}
Число различных 5-значных четных чисел, которые можно составить из всех цифр числа 25634, равно
24
72
48
60
Pасстояние между вершинами А и В в графе с заданными длинами ребер равно 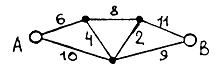

23
19
25
17
Число вершин в графе переходов автомата с входным алфавитом {a, b, c}, выходным алфавитом {d, е} и 7 состояниями равно
6
12
7
42
Префиксными кодами являются
{a: 01, b: 011, c: 1010, d: 11}
{a: 01, b: 101, c: 110}
{a: 001, b: 01, c: 101, d: 10}
{a: 001, b: 10, c: 110, d: 111}
Количество различных четырехбуквенных комбинаций, которые можно составить из букв, входящих в слово «ДОСКА» (все буквы в комбинации различны), равно
120
5
21
112
Для ориентированного графа, изображенного на рисунке, 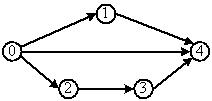 полный путь может иметь вид …
полный путь может иметь вид …
 полный путь может иметь вид …
полный путь может иметь вид …Рассматривается алфавит, состоящий из букв, входящих в слово «маршрут». С помощью этого алфавита невозможно закодировать слово
ШРАТР
ШТУРМ
ТЬМА
ШАУРМА
Канонические уравнения автомата выражают текущее выходное значение через
предыдущее значение на входе и предыдущее внутреннее состояние
текущее значение на входе и текущее внутреннее состояние
предыдущее значение на входе и текущее внутреннее состояние
текущее значение на входе и предыдущее внутреннее состояние
Число дуг (без склеивания) в графе переходов автомата с входным алфавитом {a, b}, выходным алфавитом {a, b, c, d} и 5 состояниями равно
5
10
40
20