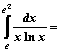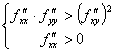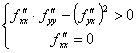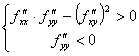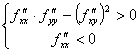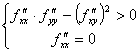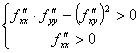Математика (СП)
Функция 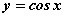 обладает следующими свойствами
обладает следующими свойствами
Область определения 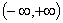 ; область значений
; область значений 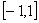 ; ограниченная; четная
; ограниченная; четная
Область определения 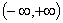 ; область значений
; область значений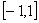 ; ограниченная; нечетная
; ограниченная; нечетная
Область определения 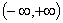 ; область значений
; область значений 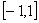 ; неограниченная; нечетная
; неограниченная; нечетная
Область определения 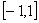 ; область значений
; область значений 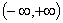 ; ограниченная; четная
; ограниченная; четная
Площадь области, ограниченной линиями 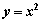 и
и 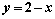 , вычисляется с помощью определенного интеграла
, вычисляется с помощью определенного интеграла
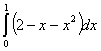 .
.Функция 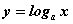 при
при 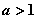 обладает следующими свойствами
обладает следующими свойствами
Область определения 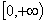 ; область значений
; область значений 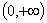 ; убывающая;
; убывающая; 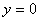 при
при 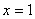
Область определения 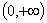 ; область значений
; область значений 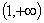 ; возрастающая;
; возрастающая; 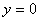 при
при 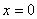
Область определения 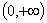 ; область значений
; область значений 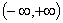 ; возрастающая;
; возрастающая; 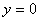 при
при 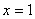
Область определения 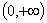 ; область значений
; область значений 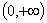 ; убывающая;
; убывающая; 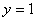 при
при 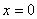 .
.
Среди функций 1) 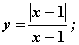 2)
2) 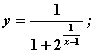 3)
3) 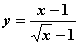 ; 4)
; 4) 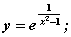 5)
5) 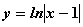 в точке
в точке 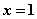 разрыв второго рода имеют функции
разрыв второго рода имеют функции
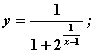 3)
3) 2, 3
4, 5
2, 5
1, 4
Для того, чтобы стационарная точка 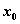 дважды дифференцируемой функции
дважды дифференцируемой функции 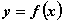 была точкой локального минимума, достаточно чтобы
была точкой локального минимума, достаточно чтобы
В области определения число точек экстремума функции 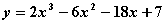 равно
равно
1
2
точек экстремума функции нет
0
Площадь области, ограниченной линиями 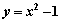
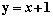 , вычисляют с помощью определенного интеграла
, вычисляют с помощью определенного интеграла
Приращение 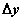 и дифференциал
и дифференциал 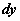 функции
функции 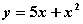 при
при 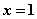 и
и 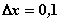 равны соответственно
равны соответственно
0,41 и 0,4
0,61 и 0,6
0,51 и 0,5
0,71 и 0,7
Точка 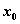 называется критической точкой функции
называется критической точкой функции 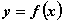 , если
, если
Множество 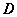 является областью определения, а множество
является областью определения, а множество 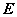 - областью значений функции
- областью значений функции 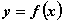 . Областью определения функции
. Областью определения функции 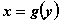 , обратной к данной является множество
, обратной к данной является множество
Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 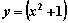 , у=0, х=1, х=2 вычисляют с помощью интеграла
, у=0, х=1, х=2 вычисляют с помощью интеграла
Функция 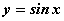 обладает следующими свойствами
обладает следующими свойствами
Область определения 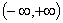 ; область значений
; область значений 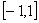 ; неограниченная; четная
; неограниченная; четная
Область определения 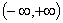 ; область значений
; область значений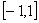 ; ограниченная; четная
; ограниченная; четная
Область определения 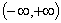 ; область значений
; область значений 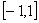 ; ограниченная; нечетная
; ограниченная; нечетная
Область определения 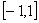 ; область значений
; область значений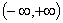 ; ограниченная; нечетная
; ограниченная; нечетная
Среди функций: 1) 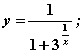 2)
2) 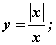 3)
3) 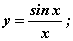 4)
4) 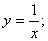 5)
5) 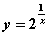 в точке
в точке 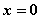 устранимый разрыв имеют функции
устранимый разрыв имеют функции
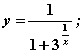 2)
2) 1, 3
3
2, 3,4
3, 4
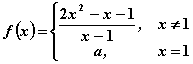 будет непрерывной при
будет непрерывной при