Математика (СП)
Функция 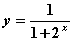 в точке
в точке 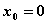
имеет разрыв второго рода
имеет устранимый разрыв
непрерывна
имеет разрыв первого рода
Функция 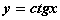 обладает следующими свойствами
обладает следующими свойствами
Периодическая, с периодом 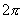 ; убывающая; неограниченная; четная
; убывающая; неограниченная; четная
Периодическая, с периодом 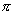 ; возрастающая; ограниченная; четная
; возрастающая; ограниченная; четная
Периодическая, с периодом 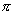 ; возрастающая; неограниченная; нечетная
; возрастающая; неограниченная; нечетная
Периодическая, с периодом 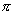 ; убывающая; неограниченная; нечетная
; убывающая; неограниченная; нечетная
Функция 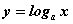 при
при 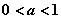 обладает следующими свойствами
обладает следующими свойствами
Область определения 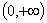 ; область значений
; область значений 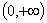 ; монотонно убывает
; монотонно убывает 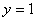 при
при 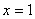
Область определения 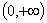 ; область значений
; область значений 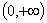 ; монотонно возрастает,
; монотонно возрастает, 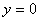 при
при 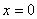
Область определения 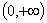 ; область значений
; область значений 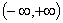 ; монотонно убывает;
; монотонно убывает; 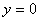 при
при 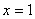
Область определения 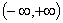 ; область значений
; область значений 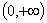 ; монотонно убывает;
; монотонно убывает; 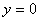 при
при 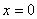
Разность значений функций 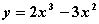 в точках локального максимума и локального минимума равна
в точках локального максимума и локального минимума равна
0
1
2
-1
Среди функций: 1) 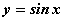 ; 2)
; 2) 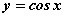 ; 3)
; 3) 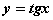 ; 4)
; 4) 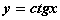 на интервале
на интервале 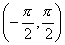 возрастающими являются
возрастающими являются
1, 3
1, 4
1, 2, 4
1, 2, 3
Длина дуги кривой y=lnx от точки М(1,0) до точки М(е,1) вычисляется с помощью интеграла
Длину дуги кривой 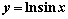 от точки с абсциссой
от точки с абсциссой 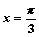 до точки с абсциссой
до точки с абсциссой 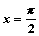 вычисляют с помощью интеграла
вычисляют с помощью интеграла
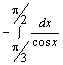
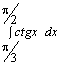
Для того, чтобы стационарная точка 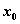 дважды дифференцируемой функции
дважды дифференцируемой функции 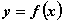 была точкой максимума, достаточно чтобы
была точкой максимума, достаточно чтобы
Среди функций: 1) 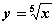 ; 2)
; 2) 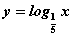 ; 3)
; 3) 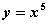 ; 4)
; 4) 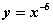 ; 5)
; 5) 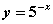 ; 6)
; 6) 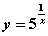 взаимно обратными являются следующие пары
взаимно обратными являются следующие пары
(3,4) и (4,5)
(5,6)
(1,3) и (2,5)
(1,4)
Для функции 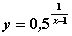 односторонние пределы в точке
односторонние пределы в точке 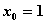 равны
равны
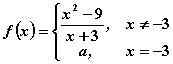 будет непрерывной при
будет непрерывной при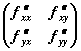 для функции
для функции