Математика (курс 11)
Спектр линейного оператора А в евклидовом пространстве R2 A = 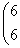
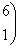 :
:
{-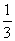 ; 0,1}
; 0,1}
{-10;3}
{-0,1; 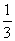 }
}
{-3;10}
Уравнение x(t) - 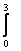
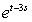 x(s)ds = et является интегральным уравнением
x(s)ds = et является интегральным уравнением
Вольтерра первого рода
Фредгольма первого рода
Вольтерра второго рода
Фредгольма второго рода
Применение алгоритма ортогонализации Грама-Шмидта к системе векторов u {-1,0,1} , v {5,4,-3} евклидова пространства R3 даёт векторы u,w, причем вектор w равен
{4,1,1}
{1,4,4}
{1,1,4}
{1,4,1}
Расстояние от f(x) до g(x) в пространстве С [a,b] определяется по формуле: r(f(x),g(x)) = 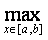
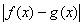 Тогда расстояние между х3 + 3х2 + 1 и 24х в С [0,3] равно
Тогда расстояние между х3 + 3х2 + 1 и 24х в С [0,3] равно
35
15
27
17
Косинус угла между элементами f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: cos(f(x),g(x)) = 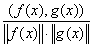 ; (f(x),g(x)) =
; (f(x),g(x)) = 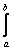 f(x)×g(x)dx ;
f(x)×g(x)dx ; 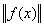 =
= 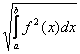 . Тогда косинус угла между элементами x2 и x3 в пространстве L2 [0,2] равен
. Тогда косинус угла между элементами x2 и x3 в пространстве L2 [0,2] равен
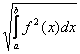 . Тогда косинус угла между элементами x2 и x3 в пространстве L2 [0,2] равен
. Тогда косинус угла между элементами x2 и x3 в пространстве L2 [0,2] равен- 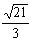
- 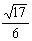
Если j(х) является отображением отрезка [a,b] в себя и имеет непрерывную производную j¢(х) на отрезке [a,b], то коэффициент сжатия оценивается по формуле q = 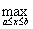 êj¢(х) ê . Тогда отображение j(х) = cosx - 1 отрезка [-
êj¢(х) ê . Тогда отображение j(х) = cosx - 1 отрезка [-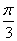 ;
;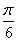 ] в себя является сжатым с коэффициентом сжатия
] в себя является сжатым с коэффициентом сжатия
-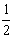
Коэффициент ряда Фурье элемента f(x) = x по ортогональной системе 1, coskx, sinkx, k = 1,2,… пространства L2[-p,p] при sinx равен
2
1
4
0
Если j(х) является отображением отрезка [a,b] в себя и имеет непрерывную производную j¢(х) на отрезке [a,b], то коэффициент сжатия оценивается по формуле q = 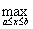 êj¢(х) ê . Тогда отображение j(х) = e 0,5x - 1 отрезка [-0,5;0,5] в себя является сжатым с коэффициентом сжатия
êj¢(х) ê . Тогда отображение j(х) = e 0,5x - 1 отрезка [-0,5;0,5] в себя является сжатым с коэффициентом сжатия
0,5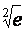
0,5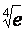
Норма В интегрального оператора Фредгольма с ядром К(t,s) в пространстве L2[a,b] определяется по формуле В = 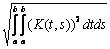 Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = et+s в пространстве L2[0,ln2] равна
Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = et+s в пространстве L2[0,ln2] равна
1,5
2,5
1,9
0,5
Косинус угла между элементами f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: cos(f(x),g(x)) = 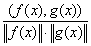 ; (f(x),g(x)) =
; (f(x),g(x)) = 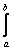 f(x)×g(x)dx ;
f(x)×g(x)dx ; 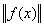 =
= 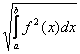 . Тогда косинус угла между элементами x и x3 в пространстве L2 [0,3] равен
. Тогда косинус угла между элементами x и x3 в пространстве L2 [0,3] равен
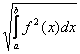 . Тогда косинус угла между элементами x и x3 в пространстве L2 [0,3] равен
. Тогда косинус угла между элементами x и x3 в пространстве L2 [0,3] равен- 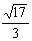
- 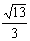
Уравнение 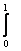 ( t6+s6)x(s)ds = sint является интегральным уравнением
( t6+s6)x(s)ds = sint является интегральным уравнением
Фредгольма первого рода
Вольтерра второго рода
Фредгольма второго рода
Вольтерра первого рода
Наилучшее линейное приближение функции x3 в пространстве L2[-1,1] равно
1 + 0,6x
1 + 0,4x
0,6x
0,4x
Применение алгоритма ортогонализации Грама-Шмидта к системе векторов u {1,1,0} , v {3,-7,-2} евклидова пространства R3 даёт векторы u,w, причем вектор w равен
{5,-5,-2}
{-2,5,5}
{-5,2,5}
{-5,2,-2}
Коэффициент ряда Фурье элемента f(x) = x2 по ортогональной системе 1, coskx, sinkx, k = 1,2,… пространства L2[-p,p] при сos2x равен
2
0
1
-1
Уравнение 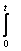 (2t2 - sins)x(s)ds = tgt является интегральным уравнением
(2t2 - sins)x(s)ds = tgt является интегральным уравнением
Вольтерра первого рода
Фредгольма первого рода
Вольтерра второго рода
Фредгольма второго рода
Спектр линейного оператора А в евклидовом пространстве R2 A = 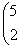
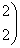 :
:
{1;6}
{-6;-1}
{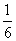 ; 1}
; 1}
{-1;-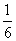 }
}
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества (-1,+¥) является
(-1,+ ¥)
(-¥,-1]
[-1,+ ¥)
[-1,+ ¥]
Уравнение х(t) - 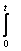 ln(t2s - s3)x(s)ds = et является интегральным уравнением
ln(t2s - s3)x(s)ds = et является интегральным уравнением
Вольтерра первого рода
Фредгольма второго рода
Вольтерра второго рода
Фредгольма первого рода
Многочлены Лежандра: Р0 = 1, Р1(х) = х, Р2 = 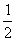 (3х2 - 1). Разложение элемента f(x) = 3x2 +5x +1 по многочленам Лежандра имеет вид:
(3х2 - 1). Разложение элемента f(x) = 3x2 +5x +1 по многочленам Лежандра имеет вид:
f(x) = P0 + 3P1 + 5P2
f(x) = 3P0 + 5P1 + P2
f(x) = 5P0 + 2P1 + 5P2
f(x) = 2P0 + 5P1 + 2P2
Норма В интегрального оператора Фредгольма с ядром К(t,s) в пространстве L2[a,b] определяется по формуле В = 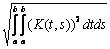 Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = (ts)6 в пространстве L2[0,1] равна
Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = (ts)6 в пространстве L2[0,1] равна
Норма оператора А (z1,z2,z3) = ( (a1+b1i)z1, (a2+b2i)z2, (a3+b3i)z3 ) на унитарном пространстве С3 определяется по формуле 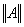 = max{
= max{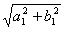 ,
,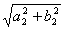 ,
,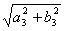 }. Тогда норма оператора А (z1,z2,z3) = ( (-3-i)z1, (3-4i)z2, (2+2i)z3 ) равна
}. Тогда норма оператора А (z1,z2,z3) = ( (-3-i)z1, (3-4i)z2, (2+2i)z3 ) равна
5
4
Наилучшее линейное приближение функции cosx в пространстве L2[-1,1] равно
2sin1
2cos1
cos1
sin1
Уравнение 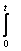 ln(t2+ts+s2)x(s)ds = t + 3 является интегральным уравнением
ln(t2+ts+s2)x(s)ds = t + 3 является интегральным уравнением
Фредгольма второго рода
Вольтерра второго рода
Вольтерра первого рода
Фредгольма первого рода
Расстояние от f(x) до g(x) в пространстве С [a,b] определяется по формуле: r(f(x),g(x)) = 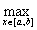
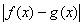 Тогда расстояние между 2х3 + 2 и 3x2 + 12х в С[-1,3] равно
Тогда расстояние между 2х3 + 2 и 3x2 + 12х в С[-1,3] равно
8
9
18
19
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества всех рациональных чисел является множество
всех вещественных чисел
всех рациональных чисел
Æ - пустое множество
всех иррациональных чисел
Норма В интегрального оператора Фредгольма с ядром К(t,s) в пространстве L2[a,b] определяется по формуле В = 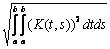 Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = sin(t)×cos(s) в пространстве L2[0,p] равна
Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = sin(t)×cos(s) в пространстве L2[0,p] равна
Интегральное уравнение Фредгольма x(t) - l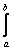 K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при l <
K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при l < 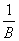 , где В =
, где В = 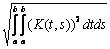 . Тогда интегральное уравнение Фредгольма x(t) - l
. Тогда интегральное уравнение Фредгольма x(t) - l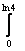 et+s x(s) ds = y(t) решается методом последовательных приближений при l, меньшем
et+s x(s) ds = y(t) решается методом последовательных приближений при l, меньшем
Норма В интегрального оператора Фредгольма с ядром К(t,s) в пространстве L2[a,b] определяется по формуле В = 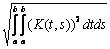 . Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = t3s4 в пространстве L2[0,1] равна
. Тогда норма интегрального оператора Фредгольма с ядром К(t,s) = t3s4 в пространстве L2[0,1] равна
Уравнение х(t) -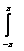 cos(t+2s)x(s)ds = cos2t является интегральным уравнением
cos(t+2s)x(s)ds = cos2t является интегральным уравнением
Вольтерра второго рода
Фредгольма второго рода
Фредгольма первого рода
Вольтерра первого рода
Интегральное уравнение Фредгольма x(t) - l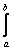 K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при l <
K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при l < 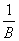 , где В =
, где В = 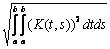 . Тогда интегральное уравнение Фредгольма x(t) - l
. Тогда интегральное уравнение Фредгольма x(t) - l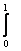 (ts)3 x(s) ds = y(t) решается методом последовательных приближений при l, меньшем
(ts)3 x(s) ds = y(t) решается методом последовательных приближений при l, меньшем
9
8
6
7
Многочлены Лежандра: Р0 = 1, Р1(х) = х, Р2 = 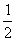 (3х2 - 1). Разложение элемента f(x) = -6x2 +x -5 по многочленам Лежандра имеет вид:
(3х2 - 1). Разложение элемента f(x) = -6x2 +x -5 по многочленам Лежандра имеет вид:
f(x) = -5P0 + P1 - 6P2
f(x) = -7P0 + P1 - 4P2
f(x) = -6P0 + 2P1 - 5P2
f(x) = -6P0 + P1 - 5P2
Применение алгоритма ортогонализации Грама-Шмидта к системе векторов u {0,1,-1} , v {-2,2,4} евклидова пространства R3 даёт векторы u,w, причем вектор w равен
{-3,2,3}
{-2,2,3}
{-2,3,3}
{-3,2,2}
Спектр линейного оператора А в евклидовом пространстве R2 A=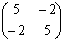
{ 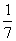 ;
; 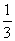 }
}
{-7;-3}
{3;7}
{- 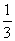 ;
; 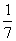 }
}
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества решений неравенства х2siny < 1 является множество решений
х2siny £ 1
х2siny = 1
х2siny > 1
х2siny ³ 1
Регулярные числа оператора А в евклидовом пространстве R2 A = 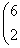
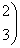 :
:
(-¥;-7) È (-7;-2) È (-2;+ ¥)
(-¥;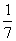 ) È (
) È (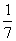 ; 0,5 ) È (0,5;+ ¥)
; 0,5 ) È (0,5;+ ¥)
(-¥;2) È (2;7) È (7;+ ¥)
(-¥;-0,5) È (-0,5; -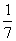 ) È (-
) È (-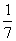 ;+ ¥)
;+ ¥)
Если j(х) является отображением отрезка [a,b] в себя и имеет непрерывную производную j¢(х) на отрезке [a,b], то коэффициент сжатия оценивается по формуле q = 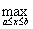 êj¢(х) ê . Тогда отображение j(х) = х3 отрезка [-0,5 ; 0,4] в себя является сжатым с коэффициентом сжатия
êj¢(х) ê . Тогда отображение j(х) = х3 отрезка [-0,5 ; 0,4] в себя является сжатым с коэффициентом сжатия
0,75
0,5
0,48
-0,75
Применение алгоритма ортогонализации Грама-Шмидта к системе векторов u {1,1,1} , v {1,2,3} евклидова пространства R3 даёт векторы u,w, причем вектор w равен
{-1,1,0}
{-1,0,1}
{0,1,-1}
{1,0,1}
Норма оператора А (z1,z2,z3) = ( (a1+b1i)z1, (a2+b2i)z2, (a3+b3i)z3 ) на унитарном пространстве С3 определяется по формуле 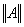 = max{
= max{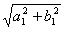 ,
,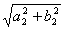 ,
,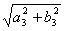 }. Тогда норма оператора А (z1,z2,z3) = ( 4z1, (3+3i)z2, (3-3i)z3 ) равна
}. Тогда норма оператора А (z1,z2,z3) = ( 4z1, (3+3i)z2, (3-3i)z3 ) равна
3
4
Косинус угла между элементами f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: cos(f(x),g(x)) = 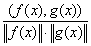 ; (f(x),g(x)) =
; (f(x),g(x)) = 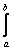 f(x)×g(x)dx ;
f(x)×g(x)dx ; 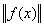 =
= 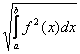 . Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
. Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
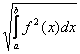 . Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен
. Тогда косинус угла между элементами x4 и 1 в пространстве L2 [0,2] равен0,8
-0,1
-0,5
0,6
Уравнение 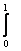
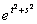 x(s)ds = 2t2 является интегральным уравнением
x(s)ds = 2t2 является интегральным уравнением
Вольтерра второго рода
Вольтерра первого рода
Фредгольма первого рода
Фредгольма второго рода
Скалярное произведение функций f(x) и g(x) в пространстве L2 [a,b] определяется по формуле: (f(x),g(x)) = 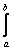 f(x)×g(x)dx. Тогда скалярное произведение элементов 3x2 и cosx3 в пространстве L2 [0,2] равно
f(x)×g(x)dx. Тогда скалярное произведение элементов 3x2 и cosx3 в пространстве L2 [0,2] равно
sin2
sin8
cos8
cos2
Коэффициент ряда Фурье элемента f(x) = x2 по ортогональной системе 1, coskx, sinkx, k = 1,2,… пространства L2[-p,p] при сosx равен
0
-5
-2
-4
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества решений неравенства ex + 3x2y4 > 1 является множество решений
ex + 3x2y4 £ 1
ex + 3x2y4 < 1
ex + 3x2y4 = 1
ex + 3x2y4 ³ 1
Регулярные числа оператора А в евклидовом пространстве R2 A = 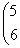
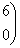 :
:
(-¥,-4) È (-4,9) È (9,+ ¥)
(-¥;0,25) È (- 0,25; 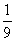 ) È (
) È (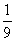 ;+ ¥)
;+ ¥)
(-¥,9) È (-9,4) È (4,+ ¥)
(-¥;-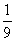 ) È (-
) È (-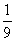 ; 0,25) È (0,25;+ ¥)
; 0,25) È (0,25;+ ¥)
Точка х Î А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества {1;2;3;…} является
{0}
{0;1;-1;2;-2;…}
Æ - пустое множество
{1;2;3;…}
Норма элемента f(x) в пространстве С [a,b] определяется по формуле: 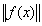 =
= 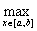
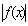 . Тогда норма элемента sinx в пространстве С [-
. Тогда норма элемента sinx в пространстве С [-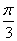 ,
,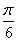 ] равна
] равна
Регулярные числа оператора А в евклидовом пространстве R2 A=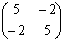
(-¥;3) È (3;7) È (7;+ ¥)
(-¥;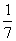 ) È (
) È (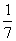 ;
;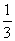 ) È (
) È (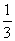 ;+ ¥)
;+ ¥)
(-¥;-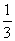 ) È (-
) È (-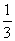 ; -
; -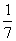 ) È (-
) È (-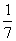 ;+ ¥)
;+ ¥)
(-¥;-7) È (-7;-3) È (-3;+ ¥)
Многочлены Лежандра: Р0 = 1, Р1(х) = х, Р2 = 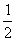 (3х2 - 1). Разложение элемента f(x) = -3x2 + 4 по многочленам Лежандра имеет вид:
(3х2 - 1). Разложение элемента f(x) = -3x2 + 4 по многочленам Лежандра имеет вид:
f(x) = -3P0 + 4P2
f(x) = 2P0 - 3P2
f(x) = 4P0 - 3P2
f(x) = 3P0 - 2P2