Линейная алгебра (курс 2)
Дана плоскость x + y + z – 6 = 0 и точки M1(1,–1,3) и M2(2,0,4)
прямая M1M2 перпендикулярна плоскости
прямая M1M2 параллельна плоскости
точка M1 удалена от плоскости на расстояние d = 1
прямая M1M2 лежит на плоскости
В сечении поверхности x2 – y2 + z2 = 0 координатной плоскостью XOY получим
эллипс
пару прямых
точку
гиперболу
Прямая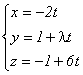 
перпендикулярна плоскости x – 2y – 3z + 9 = 0 при λ, равном
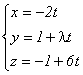перпендикулярна плоскости x – 2y – 3z + 9 = 0 при λ, равномни при каком λ
4
–4
–10
Даны плоскости 1) 2x + 6y – 3z + 14 = 0; 2) 3x + 2y – 6z + 21 = 0; 3) 6x + 3y – 2z + 7 = 0. На расстоянии d = 3 от точки M0(0,0,–7) отстоят плоскости
никакая
2, 3
1, 3
3
Дана плоскость x + y + z – 9 = 0 и точка M(3,3,3), тогда
точка М не лежит на плоскости
точка М и начало координат лежат на плоскости
точка М является проекцией начала координат на плоскость
точка М отстоит от плоскости на расстоянии 9
Прямая x = 2λt – 1, y = λt + 1, z = – t – 2 перпендикулярна плоскости 2x + y – z + 5 = 0 при λ равном ___ (число)
Установите верные соответствия между поверхностью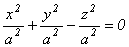 
и ее сечениями с плоскостями
и ее сечениями с плоскостямиx = a
точка
XOZ
пара пересекающихся прямых
XOY
равнобочная гипербола
и 
, имеет вид
Плоскость, проходящая через точку M1(1,–1,–1) перпендикулярно к прямой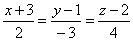 
, задается уравнением
, задается уравнением2x – 3y + 4z – 5 = 0
2x – 3y + 4z = 0
2x – 3y + 4z + 1 = 0
2x – 3y + 4z – 1 = 0
Прямая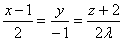 
параллельна плоскости 7x + λy – 3z + 10 = 0 при λ равном ___ (число)
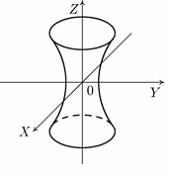
параллельна плоскости 7x + λy – 3z + 10 = 0 при λ равном ___ (число)Установите соответствие между изображением поверхности и ее названием.
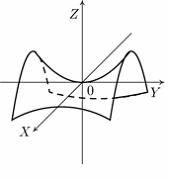
гиперболический параболоид
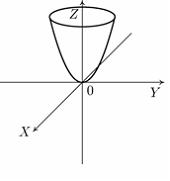
эллиптический параболоид
однополостный гиперболоид
Горловым сечением однополосного гиперболоида x2 + y2 – z2 – 4x = 0 является
окружность с центом (0,0,0) и радиусом R = 4
эллипс с центом (2,0,0) и полуосями a = 2, b = 1
эллипс с центом (0,0,0) и полуосями a = 1, b = 2
окружность с центом (2,0,0) и радиусом R = 2
Каноническое уравнение прямой, проходящей через точку M(2,0,–3), перпендикулярно плоскости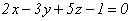 
, имеет вид
, имеет вид
равноДаны точки M1(1,1,1) и M2(0,1,1). Точка M2 является
проекцией M1 на плоскость x + y + z = 2
проекцией M1 на плоскость YOZ
основанием перпендикуляра, опущенного из M1 на плоскость YOZ
проекцией M1 на ось OX
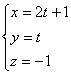
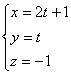
параллельна оси ___ (слово)Прямая 
перпендикулярна плоскости 2x + y – 1 = 0
имеет направляющий вектор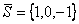 
проходит через точку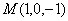 
лежит на плоскости 2x + y – 1 = 0
Уравнение x2 + y2 – z2 – 4x = 0 определяет
сфера с центом (2,0,0) и радиусом R = 2
однополостный гиперболоид с центом симметрии в точке (2,0,0)
эллипсоид с центом (2,0,0)
однополостный гиперболоид с центом симметрии в точке (0,0,0)
Даны плоскости 1) 2x + 2y – z + 6 = 0, 2) x – 2y + 2z – 6 = 0, 3) 2x + 4y – 4z – 12 = 0. Пусть d1, d2, d3 – расстояния от начала координат до каждой плоскости соответственно. Тогда
d1 = d2 = d3
d1 + d2 = d3
d3 = 2d1, d1 = d2
d2 = 2d1, d3 = d2
Плоскость x + 2y + 1 =0
параллельна плоскости XOY
перпендикулярна оси OZ
проходит через точку М(1,2,1)
параллельна оси OZ
равно
является вектор
Прямая 
пересекается с плоскостью x – y – z + 3 = 0 в точке
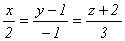пересекается с плоскостью x – y – z + 3 = 0 в точкеM(2, –1,3)
M(0,1,–2)
M(1, –1,–1)
нет точек пересечения
Прямая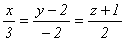 
пересекает поверхность 
в точках
пересекает поверхность 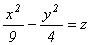в точкахпрямая не пересекает поверхность
прямая лежит на поверхности
М1(1,2,–1) и М2(0,2,–1)
в множестве точек
Уравнение x2 + z2 = 0 в пространстве определяет
точку (0,0,0)
окружность
мнимую окружность
ось OY
Даны плоскость 2x + 2y – z + 6 = 0 и точки М1(3,0,3) и М2(7,4,5). Пусть d1 – расстояние от точки М1 до плоскости, d2 – расстояние между точками М1 и М2, тогда
d1 > d2
d1 = 2d2
d2 = d1
d2 = 2d1
Укажите верные соответствия уравнений плоскостей координатным плоскостям, им параллельным
Cz + D = 0, C ≠ 0
Oyz
By + D = 0, B ≠ 0
OXz
Ax + D = 0, A ≠ 0
OXy
Уравнение плоскости, проходящей через начало координат и точк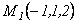и 
и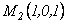 
, имеет вид
и , имеет вид
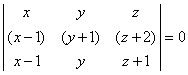
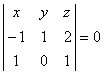
–x + 3y – z = 0
x + 3y – z = 0
Укажите верные соответствия
Ax + By + Dz = 0
уравнение плоскости в отрезках
A(x – x0) + B(y – y0) + C(z – z0) = 0
плоскость проходит через точку M0(xo, y0, z0) перпендикулярно вектору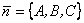 
уравнение плоскости, проходящей через начало координат
Дана прямая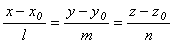 
и плоскость Ax + By + Cz + D = 0. Установите верные соответствия между их взаимным расположением и данными условиями
и плоскость Ax + By + Cz + D = 0. Установите верные соответствия между их взаимным расположением и данными условиямиAl + Bm + Cn = 0
прямая лежит в плоскости
прямая перпендикулярна плоскости
Al + Bm + Cn = 0 Ax0 + By0 + Cz0 + D = 0
прямая параллельна плоскости
Уравнение прямой, проходящей через точку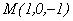 
перпендикулярно плоскости 
, имеет вид
перпендикулярно плоскости 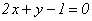, имеет вид
Плоскость z + 1 = 0 пересекает гиперболоид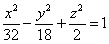 
по
погиперболе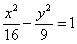 
эллипсу
гиперболе с полуосями a = 16, b = 9
эллипсу с полуосями a = 4, b = 3
Уравнение перпендикуляра, опущенного из начала координат на плоскость 3x + y – 2z +5 = 0, имеет вид
x = y = z
3x = y = – 2z
Прямая 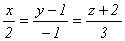пересекается с плоскостью 2x – y + 3z – 7 = 0 в точке
пересекается с плоскостью 2x – y + 3z – 7 = 0 в точкенет точек пересечения
M(0,1,–2)
M(2,0,1)
M(2,–1,3)
Установите верные соответствия
z = 0
уравнение оси OX
уравнение оси OY
уравнение плоскости XOY
Проекцией точки M1(2,1,6) на плоскость YOZ является точка
M2(2,1,0)
M2(2,0,6)
M2(2,0,0)
M2(0,1,6)
Нормаль к плоскости 2y – z + 2 = 0
параллельна оси OZ
перпендикулярна плоскости z = 0
параллельна плоскости XOY
перпендикулярна оси OX
Уравнение x2 – 4y2 = 4 в пространстве определяет
гиперболоид (однополостный)
цилиндрическую поверхность с образующими параллельными оси OZ
гиперболу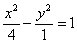 
цилиндрическую поверхность имеющей направляющей гиперболу с полуосями a = 2, b = 1; образующие параллельны оси OZ
Даны плоскости: 1) x + 2y – 2z – 4 = 0; 2) x + 2y – 2z + 8 = 0; 3) x + 2y – 2z + 2 = 0
расстояние от плоскости 3) до плоскости 1) равно 2
расстояние от плоскости 3) до плоскости 2) равно 8
плоскость 3) равноудалена от плоскостей 1) и 2)
расстояние от плоскости 3) до плоскости 2) вдвое больше расстояния до плоскости 1)
равен
Уравнение x2 + z2 – 4z + 2y = 0 определяет
гиперболический параболоид с вершиной (0,–2, 2)
параболоид вращения с осью симметрии, параллельной оси OY
эллиптический параболоид с вершиной (0,–2, 2)
Прямая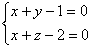 
и плоскость y – z + 5 = 0
и плоскость y – z + 5 = 0прямая лежит в плоскости
перпендикулярны
пересекаются
параллельны
Даны плоскости 1) x + 2y – 2z + 3 = 0 и 2) x + 2y – 2z – 6 = 0 и точка M0(1,1,0)
расстояние от M0 до плоскости 1) вдвое больше, чем до плоскости 2)
расстояние от M0 до плоскости 1) d1 = 6, а до плоскости 2) d2 = 3
расстояние d1 от M0 до плоскости 1) d1 = 2, а расстояние до плоскости 2) d2 = 1
точка M0 равноудалена от плоскостей 1) и 2)
Прямая x = 2λt – 1, y = λt + 1, z = – t параллельна плоскости x + 2y – 4z + 1 = 0 при λ равном ___ (число)
Плоскость y – 3 = 0 пересекает поверхность 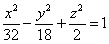по
погиперболе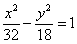 
в единственной точке (16,9,1)
параболе
эллипсу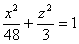 
Даны плоскост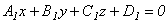и 
и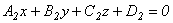 
. Укажите верные соответствия
и . Укажите верные соответствия
плоскости перпендикулярны
плоскости параллельны
плоскости совпадают
Прямая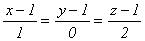 
параллельна координатной плоскости
параллельна координатной плоскостиYOZ
ни одной координатной плоскости не параллельна
XOY
XOZ
Установите соответствие между поверхностью второго порядка и ее уравнением.
Двуполостный гиперболоид
Однополостный гиперболоид
Эллипсоид
Дана плоскость x + y + z – 6 = 0 и точки M1(1,–1,3), M2(2,0,4)
расстояние от точки M2 до плоскости равно 1
прямая M1M2 лежит на плоскости
обе точки лежат на плоскости
расстояние от точки M2 до плоскости равно 0