Дифференциальное исчисление функций одной переменной
производная сложной функции
промежуточный аргумент
сложная функция от 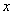 ; функция от функции; суперпозиция функций
; функция от функции; суперпозиция функций 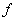 и
и 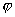
функция от 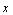
Между точками на числовой оси и действительными числами установлено соответствие
взаимно однозначное
служащее для изображения рациональных чисел
однозначное
служащее для изображения целых чисел
Теорема Лагранжа верна, если функция 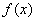
непрерывна на 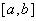
дифференцируема на 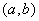
непрерывна на 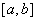 и дифференцируема по крайней мере на
и дифференцируема по крайней мере на 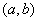
непрерывна и дифференцируема на 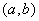
Положение точки 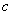 , о которой говорится в теоремах Лагранжа, Ролля, Коши, находится
, о которой говорится в теоремах Лагранжа, Ролля, Коши, находится
на середине отрезка 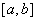
в одном из концов интервала
где-то между 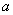 и
и 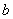 :
: 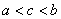
в точке 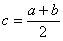
Рациональное число - это
положительное число
конечная десятичная дробь
бесконечная десятичная дробь
отношение двух целых чисел
Вертикальной асимптотой графика функции 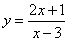 является прямая
является прямая
Для функции 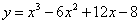 точка М(2, 0) является точкой
точка М(2, 0) является точкой
максимума
минимума
разрыва
перегиба
при некотором 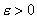 значения
значения 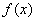 находятся в
находятся в 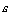 -полосе вокруг прямой
-полосе вокруг прямой 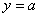
для любого 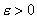 найдется такое
найдется такое 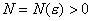 , что при
, что при 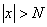 имеет место неравенство
имеет место неравенство 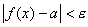 , т.е. при любом
, т.е. при любом 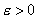 можно найти такое
можно найти такое 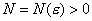 , что при
, что при 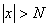 значения
значения 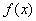 попадают в
попадают в 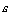 -полосу, построенную вокруг прямой
-полосу, построенную вокруг прямой 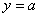
значения 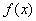 находятся в
находятся в 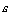 -полосе вокруг прямой
-полосе вокруг прямой 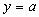
при 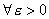 выполняется неравенство
выполняется неравенство 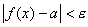
Переменная величина 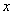 является бесконечно большой (б.б.), если
является бесконечно большой (б.б.), если
для 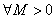 , начиная с некоторого момента в изменении
, начиная с некоторого момента в изменении 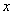 выполняется неравенство
выполняется неравенство 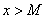
Интервалами монотонности функции 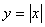 будут:
будут:
один интервал 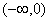
является бесконечно малой
бесконечно малая высшего порядка в сравнении с 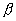
одного порядка
эквивалентны
не сравнимы
если в рассматриваемой точке 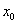 функция
функция 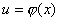 дифференцируема и функция
дифференцируема и функция 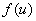 дифференцируема в точке
дифференцируема в точке 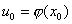
если 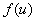 и
и 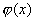 непрерывные функции
непрерывные функции
если функция 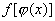 непрерывна
непрерывна
всегда
Если 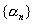 и
и 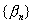 - бесконечно малые последовательности
- бесконечно малые последовательности 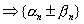 последовательность
последовательность
большего порядка малости
меньшего порядка малости
бесконечно большая
бесконечно малая
Функция 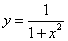 имеет интервалов монотонности -
имеет интервалов монотонности -
один
два
три
нет интервалов монотонности
Число 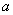 есть предел функции
есть предел функции 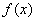 при
при 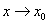 , если
, если
при 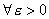 значение
значение 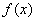 лежит в
лежит в 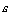 -окрестности числа
-окрестности числа 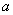
для любого 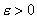 найдется
найдется 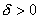 такое, что при всех
такое, что при всех 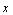 , попадающих в
, попадающих в 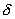 -окрестность точки
-окрестность точки 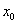 , кроме, быть может,
, кроме, быть может, 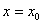 , выполняется неравенство
, выполняется неравенство 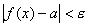
для 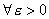 выполняется неравенство
выполняется неравенство 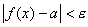
для 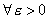
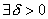 такое, что при всех
такое, что при всех 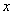 , попавших в
, попавших в 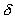 -окрестность точки
-окрестность точки 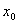 , выполняется неравенство
, выполняется неравенство 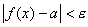
Последовательность может иметь
любое количество пределов
два различных предела
только один предел
не больше двух разных пределов
Точкой перегиба функции 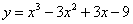 является точка с абсциссой
является точка с абсциссой
Из перечисленных определений: 1) последовательность 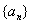 не может иметь двух различных пределов; 2) последовательность
не может иметь двух различных пределов; 2) последовательность 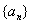 может иметь больше одного предела; 3) последовательность
может иметь больше одного предела; 3) последовательность 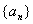 называют сходящейся, если она имеет конечный предел; 4) последовательность
называют сходящейся, если она имеет конечный предел; 4) последовательность 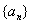 является ограниченной, если существует число
является ограниченной, если существует число 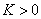 такое, что для любого
такое, что для любого 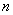
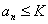 , верными будут
, верными будут
1, 3
1
1, 4
2, 3
Даны определения: 1) всякая монотонная ограниченная последовательность имеет предел; 2) последовательность 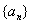 называется монотонной, если она является убывающей; 3) последовательность
называется монотонной, если она является убывающей; 3) последовательность 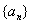 называется невозрастающей, если
называется невозрастающей, если 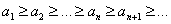 ; 4) последовательность
; 4) последовательность 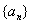 является возрастающей, если
является возрастающей, если 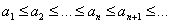
1
3, 4
2, 3
1, 3
Число 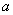 есть предел переменной величины
есть предел переменной величины 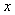 , если
, если
значения 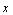 лежат в
лежат в 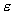 -окрестности
-окрестности 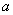
выполняется неравенство 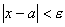
какое бы (сколь угодно малое) число 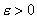 мы ни взяли, начиная с некоторого момента в изменении
мы ни взяли, начиная с некоторого момента в изменении 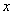 будет выполняться неравенство
будет выполняться неравенство 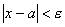
значения 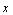 лежат в интервале
лежат в интервале 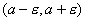
Общее геометрическое содержание теорем Ролля, Лагранжа, Коши:
касательная всегда параллельна хорде
касательная в некоторой точке кривой параллельна оси 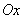
между двумя корнями функции лежит корень производной
на кривой найдется точка, в которой касательная параллельна хорде, стягивающей концы кривой
Последовательность 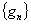 , при
, при 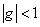 является
является
неограниченной
ограниченной
бесконечно большой
бесконечно малой
Последовательность 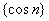 является
является
бесконечно малой
бесконечно большой
неограниченной
ограниченной
Для функции 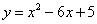 точка М (3, - 4) является точкой
точка М (3, - 4) является точкой
минимума
максимума
перегиба
разрыва
Если 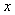 и
и 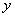 - две переменные величины, причем
- две переменные величины, причем 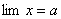 ,
, 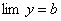 , то
, то 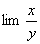 есть
есть
не определен
не связан с 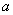 и
и 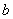
Действительные числа - это
целые числа
положительные числа
рациональные и иррациональные, положительные и отрицательные числа и число нуль
числа, которые действительно существуют
Свойство инвариантности формы записи дифференциала функции 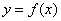 означает, что
означает, что
во всех случаях дифференциал является главной частью приращения функции
дифференциал 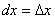
форма записи дифференциала 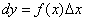 сохраняется, когда
сохраняется, когда 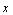 перестает быть независимой переменной
перестает быть независимой переменной
форма записи дифференциала 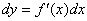 не зависит от того, будет ли
не зависит от того, будет ли 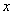 независимой переменной или функцией
независимой переменной или функцией 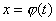 от другой переменной
от другой переменной
Для функции 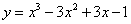 точка М (1, 0) является точкой
точка М (1, 0) является точкой
минимума
перегиба
разрыва
максимума
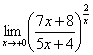 равен
равен