Вычислительная математика (курс 1)
Операции над числами в компьютере выполняются точно, если эти числа являются
целыми
рациональными
десятичными
двоичными
Дана система уравнений 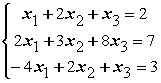 . Для сходимости итерационного метода ее надо записать в виде
. Для сходимости итерационного метода ее надо записать в виде
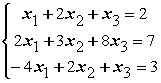 . Для сходимости итерационного метода ее надо записать в виде
. Для сходимости итерационного метода ее надо записать в виде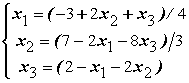
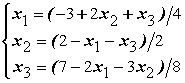
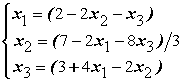
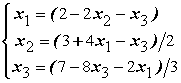
43. Даны линейные системы 1)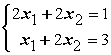 2)
2)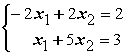 3)
3)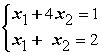 4)
4)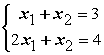 Свойством диагонального преобладания обладают системы А) только 3 В) 2 и 4
Свойством диагонального преобладания обладают системы А) только 3 В) 2 и 4
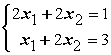 2)
2)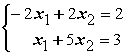 3)
3)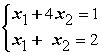 4)
4)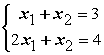 Свойством диагонального преобладания обладают системы А) только 3 В) 2 и 4
Свойством диагонального преобладания обладают системы А) только 3 В) 2 и 4A – нет, B - да
A – да, B – да
A – нет, B – нет
A – да, B - нет
Система линейных уравнений методом Гаусса приведена к треугольному виду 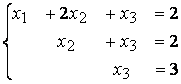 Сумма решений этой системы
Сумма решений этой системы 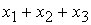 равна _____ (целое число)
равна _____ (целое число)
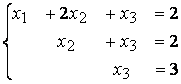 Сумма решений этой системы
Сумма решений этой системы Задана линейная система уравнений с симметричной матрицей 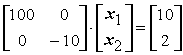 . Ее степень обусловленности равна ____(целое число)
. Ее степень обусловленности равна ____(целое число)
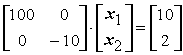 . Ее степень обусловленности равна ____(целое число)
. Ее степень обусловленности равна ____(целое число)Для величин x = 2 и y = 8 известны относительные погрешности δ(x)=0,01 и δ(y) = 0,02. Относительная погрешность суммы δ(x + y) равна _________ (укажите число с точностью до 0,001)
Верны ли утверждения? Возможны следующие виды погрешностей: A) чередующиеся В) относительные
A – нет, B - да
A – да, B – да
A – нет, B – нет
A – да, B - нет
Укажите соответствие между примерами матриц и их названием
трехдиагональная
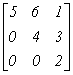
нижняя треугольная
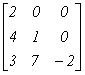
верхняя треугольная
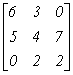
К прямым методам решения систем линейных уравнений относятся методы
Жордана
Гаусса
Зейделя
LU-разложения
Ньютона
В виде, удобном для итераций, записаны системы линейных уравнений А) 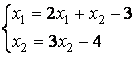 B)
B) 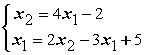
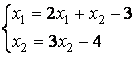 B)
B) 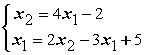
A – да, B – да
A – да, B - нет
A – нет, B - да
A – нет, B – нет
Алгоритм называется неустойчивым, если малые изменения исходных данных и погрешности округления приводят к __________изменению окончательных результатов
Для матрицы A = 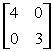 условия диагонального преобладания _______ (слово)
условия диагонального преобладания _______ (слово)
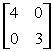 условия диагонального преобладания _______ (слово)
условия диагонального преобладания _______ (слово)К прямым методам решения систем линейных уравнений относятся методы
Гаусса
Ньютона
Зейделя
LU-разложения
Существуют следующие итерационные методы для решения систем линейных уравнений метод________
Гаусса
простой итерации
Ньютона
Зейделя
Для величин x = 2 и y = 5 известны относительные погрешности δ(x)=0,005 и δ(y) = 0,002. Относительная погрешность частного δ(x ∕ y) равна _________ (укажите число с точностью до 0,001)
Для обратного хода метода Гаусса подготовлены следующие системы уравнений 1) 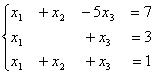 2)
2) 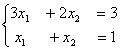 3}
3} 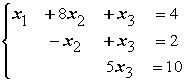
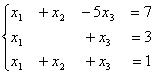 2)
2) 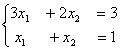 3}
3} 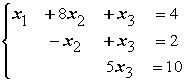
3
только 2
1 и 2
2 и 3
Обобщенное решение переопределенных систем линейных уравнений (как совместных, так и несовместных) можно найти методом
Ньютона
интерполяции
наименьших квадратов
Зейделя
При решении систем линейных уравнений можно использовать итерационные методы
Зейделя
простой итерации
LU разложения
Гаусса
Для величин x = 2 и y = 1 известны относительные погрешности: δ(x) = 0,001 и δ(y) = 0,002. Относительная погрешность разности δ(x – y) равна (число с тремя знаками после запятой)
Для линейной системы уравнений 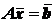 известно LU – разложение матрицы A = LU. Порядок матрицы A равен 3. Тогда порядок каждой системы с треугольными матрицами, к которым сводится решение исходной системы уравнений, равно ______ (целое число)
известно LU – разложение матрицы A = LU. Порядок матрицы A равен 3. Тогда порядок каждой системы с треугольными матрицами, к которым сводится решение исходной системы уравнений, равно ______ (целое число)
Заданы системы линейных уравнений 1) 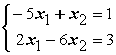 ; 2)
; 2) 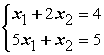 ; 3)
; 3) 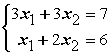 Свойством диагонального преобладания обладают матрицы систем
Свойством диагонального преобладания обладают матрицы систем
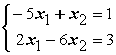 ; 2)
; 2) 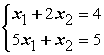 ; 3)
; 3) 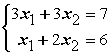 Свойством диагонального преобладания обладают матрицы систем
Свойством диагонального преобладания обладают матрицы систем2 и 3
1 и 3
только 3
только 2
Абсолютные погрешности величин x и y равны ∆x = 0,4 и ∆y =0,3. Абсолютная погрешность разности ∆(x – y) будет равна ___ (число с одним знаком после запятой)
Приведите в соответствие формулы решения линейной системы уравнений и методы итерации, где они используются
метод простой итерации
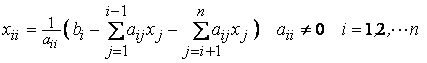
метод Зейделя
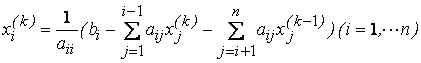
приведение к виду, удобному для итераций

Для величин x и z заданы их абсолютные погрешности: ∆(x) = 0,02; ∆(z) = 0,07 . Тогда абсолютная погрешность величины ∆(x− z) будет равна ________ (число с двумя знаками после запятой)
К неценовым факторам, определяющим объем спроса, относятся
инфляционные ожидания покупателей
доходы потребителей
новые технологии производства
цены на другие товары
число продавцов
Число 623 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление
62,3
623
6,23
0,623∙103
Верны ли утверждения? В методе Гаусса решения систем линейных уравнений используются следующие виды матриц: А) верхняя треугольная В) симметричная
A – нет, B - да
A – нет, B – нет
A – да, B – да
A – да, B - нет
Для величин x и y заданы абсолютные погрешности: Δ(x) = 0,01 и Δ(y) =1,5. Тогда абсолютная погрешность разности Δ(x−y) равна ________ (число с двумя знаками после запятой)
Для величин x = 5 и y = 1 известны абсолютные погрешности ∆(x) = 0,001 и ∆(y) = 0,002. Абсолютная погрешность частного ∆(x/y) равна _________ (укажите число с точностью до 0,0001)
Важность задач решения систем линейных уравнений заключается в том, что
они используются при переводе чисел из десятичной системы счисления в двоичную
они используются при оценке ошибок погрешностей округления
при решении нелинейных задач часто конструируются алгоритмы, основанные на последовательном решении линейных систем
эти задачи встречаются чаще всего в приложениях
к ним, как правило, сводится численное решение дифференциальных уравнений
Заданы матрицы 1) 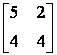 , 2)
, 2) 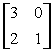 , 3)
, 3) 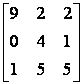 Условиям диагонального преобладания удовлетворяют матрицы
Условиям диагонального преобладания удовлетворяют матрицы
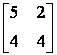 , 2)
, 2) 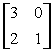 , 3)
, 3) 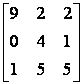 Условиям диагонального преобладания удовлетворяют матрицы
Условиям диагонального преобладания удовлетворяют матрицытолько 2
2 и 3
1
1 и 3
Приведите соответствие между итерационными формулами решения систем линейных уравнений и результатом их применения
метод Зейделя для системы 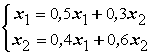
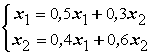
расходится
метод итераций для линейной системы 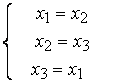
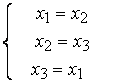
приводит к зацикливанию
метод итераций для линейной системы 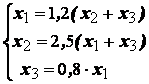
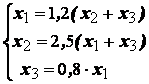
сходится при любом начальном приближении
Заданы системы линейных уравнений 1) 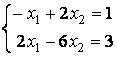 ; 2)
; 2) 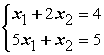 ; 3)
; 3) 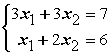 Свойством диагонального преобладания обладают матрицы систем А) 1 и 2 B) 3
Свойством диагонального преобладания обладают матрицы систем А) 1 и 2 B) 3
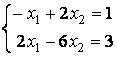 ; 2)
; 2) 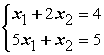 ; 3)
; 3) 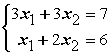 Свойством диагонального преобладания обладают матрицы систем А) 1 и 2 B) 3
Свойством диагонального преобладания обладают матрицы систем А) 1 и 2 B) 3A – да, B – да
A – да, B - нет
A – нет, B - да
A – нет, B – нет
В компьютере могут быть представлены числа:
рациональные
иррациональные
целые
десятичные
Для решения систем линейных уравнений можно использовать методы
Лежандра
Ньютона
прямые
итерационные
Заданы матрицы 1) 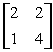 , 2)
, 2) 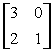 , 3)
, 3) 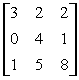 Условиям диагонального преобладания удовлетворяют матрицы
Условиям диагонального преобладания удовлетворяют матрицы
 , 2)
, 2) 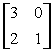 , 3)
, 3)  Условиям диагонального преобладания удовлетворяют матрицы
Условиям диагонального преобладания удовлетворяют матрицытретья
вторая и третья
первая и вторая
первая
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: A) Для хорошо обусловленных систем малые ошибки в задании правых частей и коэффициентов системы приводят к малым ошибкам в решении B) Метод Гаусса является итерационным методом
A – да, B – да
A – да, B - нет
A – нет, B - да
A – нет, B – нет
Для величин x = 10 и y = 20 известны относительные погрешности δ(x)=0,005 и δ(y) = 0,003. Относительная погрешность произведения δ(x ∙ y) равна (число с тремя знаками после запятой)
Выбор начального приближения на сходимость метода Зейделя при решении систем линейных уравнений
не влияет
не влияет, если матрица является ленточной
влияет, если матрица несимметричная
влияет, если матрица не является верхней треугольной
Укажите соответствие между наименованиями эффектов потребительского поведения и их содержанием
эффект присоединения к большинству
эффект, который имеет место в тех случаях, когда потребителем движет желание не быть похожим на других, что приводит к тому, что индивидуальный спрос некоторых людей падает при росте рыночного спроса
эффект демонстративного поведения
эффект, который возникает, когда индивидуум покупает блага, недоступные по цене для других, что делает эти товары престижными и подчеркивает социальный статус их владельца
эффект сноба
эффект, который проявляется, когда поведение потребителя диктуется желанием не отставать в потреблении от других
Значительная потеря точности при выполнении арифметических операций на ЭВМ происходит при ______ близких чисел
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: А) метод итераций Зейделя сходится всегда B) метод простой итерации сходится, если все коэффициенты матрицы системы меньше единицы
A – да, B - нет
A – да, B – да
A – нет, B – да
A – нет, B – нет
Для величин x = 1 и y = 2 известны абсолютные погрешности: ∆(x) = 0,001 и ∆(y) = 0,005. Абсолютная погрешность произведения ∆(x∙y) равна _______ (число с тремя знаками после запятой )
Существуют следующие подходы к оценке погрешностей округления при решении задачи на компьютерах
подходы, использующие статистические методы оценки влияния округления
сравнение результатов при решении задачи с обычной и двойной точностью
использование функций комплексного переменного
подходы, использующие интегральное исчисление
на каждом шаге находится интервал, в котором лежит правильное решение (область ответа)
Метод Гаусса заключается в сведении исходной матрицы системы к эквивалентному виду, где матрица преобразованной системы является
ленточной матрицей
верхней треугольной матрицей
диагональной матрицей
симметричной матрицей
Матрица A = 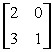 называется
называется
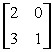 называется
называетсядиагональной
нижней треугольной
верхней симметричной
верхней треугольной
Даны линейные системы 1)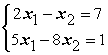 ; 2)
; 2)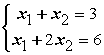 ; 3)
; 3)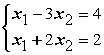 ; 4)
; 4)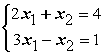 Свойством диагонального преобладания обладают системы
Свойством диагонального преобладания обладают системы
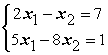 ; 2)
; 2)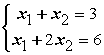 ; 3)
; 3)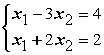 ; 4)
; 4)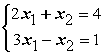 Свойством диагонального преобладания обладают системы
Свойством диагонального преобладания обладают системы3 и 4
1, 3 и 4
1 и 2
1 и 4
Укажите соответствие между видами погрешностей и их особенностями
погрешность численного метода
неустранимая
вычислительная погрешность
обусловлена округлением результатов
погрешность математической модели
регулируемая
Верны ли утверждения? Для систем линейных уравнений справедливы следующие утверждения: А) метод итераций Зейделя сходится, если матрица системы обладает свойством диагонального преобладания B) метод простой итерации сходится, если все коэффициенты матрицы положительны
A – да, B – да
A – да, B - нет
A – нет, B – нет
A – нет, B – да
На сходимость итерационного метода решения систем линейных уравнений могут влиять методы
нижней релаксации
Ньютона
верхней релаксации
Гаусса