Математика (курс 10)
В пространстве многочленов степени 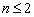 задан оператор дифференцирования
задан оператор дифференцирования 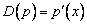 и функция
и функция 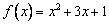 . Координаты образа
. Координаты образа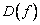 по базису
по базису 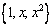 равны
равны
(0, 2, 3)
(2, 3, 0)
(3, 2, 0)
(0, 3, 2)
Если 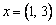 и
и 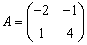 - матрица линейного преобразования А, то координаты образа
- матрица линейного преобразования А, то координаты образа 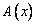 равны
равны
(-5, -11)
(-5, 13)
(-5, 11)
(1, 11)
Квадратичная форма 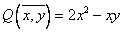 является
является
положительно определенной
неотрицательно определенной
отрицательно определенной
знаконеопределенной
Квадратичная форма 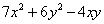 является
является
положительно определенной
неположительно определенной
неотрицательно определенной
отрицательно определенной
Координаты многочлена 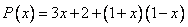 в стандартном базисе
в стандартном базисе 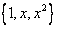 равны
равны
(3, 3, -1)
(3, 2, -1)
(-1, 3, 3)
(3, 2, 1)
Квадратичная форма 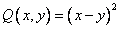 является
является
неотрицательно определенной
отрицательно определенной
положительно определенной
знаконеопределенной
Даны системы уравнений 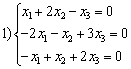 ,
, 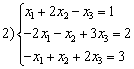 ,
, 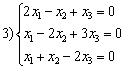 ,
, 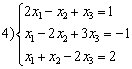 . Линейные подпространства образуют множества решений систем
. Линейные подпространства образуют множества решений систем
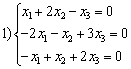 ,
, 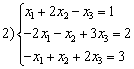 ,
, 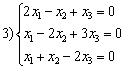 ,
, 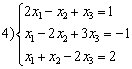 . Линейные подпространства образуют множества решений систем
. Линейные подпространства образуют множества решений систем1, 2
3, 4
2, 4
1, 3
Координаты многочлена 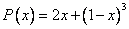 по базису
по базису 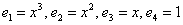 равны
равны
(1, 2, 0, 0)
(2, 1, 1, 3)
(1, -1, 3, -1)
(-1, 3, -1, 1)
Матрица перехода от стандартного базиса 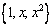 в пространстве многочленов к базису
в пространстве многочленов к базису 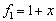 ,
, 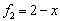 ,
, 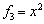 равна
равна
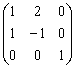
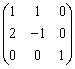
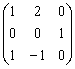
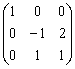
Если 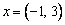 и матрица линейного преобразования
и матрица линейного преобразования 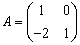 , то координаты образа
, то координаты образа 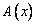 равны
равны
(1, -5)
(-7, 3)
(2, 5)
(-1, 5)
В пространстве многочленов степени 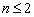 задан оператор дифференцирования
задан оператор дифференцирования 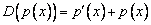 . Его матрица в базисе
. Его матрица в базисе 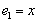 ,
, 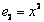 ,
, 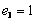 равна
равна
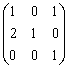
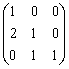
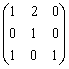
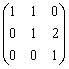
В пространстве многочленов степени 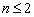 задан оператор дифференцирования
задан оператор дифференцирования 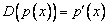 . Его матрица в базисе
. Его матрица в базисе 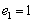 ,
, 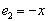 ,
, 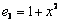 равна
равна
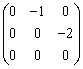
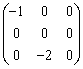
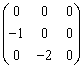
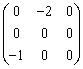
 . Базис в R3 образуют векторы
. Базис в R3 образуют векторы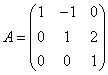 имеет вид
имеет вид