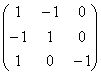Алгебра и геометрия (курс 1)

Множество решений системы Ax̅=0̅ (А – квадратная матрица порядка n) представляет собой _____________ в Rⁿ.

Квадратичная форма Q(x,y) = (x – y)² является:

В пространстве многочленов степени n ≤ 2 задан оператор 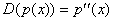 и многочлен 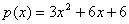. Координаты образа D(p(x)) в базисе  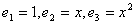равна:

Если А – линейный оператор в линейном пространстве V, т.е. А: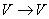, а вектор x – произвольный вектор, 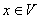, то вектор y=A(x) называют ______________ вектора x.

Произведение модулей векторов a̅ и b̅ на косинус угла j между ними называется ______________ произведением вектора a̅ на вектор b̅

Матрица перехода от одного ортонормированного базиса евклидова пространства к другому ортонормированному базису является ______________ матрицей.

Матрицей квадратичной формы  является матрица:

Линейной комбинацией 3a̅₁ – 2a̅₂ + a̅₃ векторов a̅=(1,1,1), a̅₂=(3,1,0), a̅₃=(-1,2,-3) является вектор:

Пусть detA=1, где А – квадратная матрица 3^го порядка, тогда:

В линейном пространстве функций, непрерывных на отрезке, линейно независимой является система функций: