Многомерные распределения и предельные теоремы
Х - случайная величина, МХ = 2, DX = 3. По неравенству Чебышева
P{çX – 2ú ³ 2} £
3/16
P{çX – 2ú ³ 3} £
1/3
P{çX – 2ú ³ 4} £
0,75
X и Y - некоррелированные случайные величины. Тогда
Х и У всегда независимы
Х и У могут быть зависимы
r(X,Y) = 0;
Х и У могут иметь коэффициент корреляции равным 0,5
f(x,y) – плотность вероятности непрерывного случайного вектора (X,Y), fX(x) и fY(y) – плотности вероятностей координат этого вектора
fY(y)
f(x,y)
Î [0;¥]
fX(x)
Ковариационная матрица случайного вектора (X1,X2,…,Xn) – это матрица n x n, состоящая из элементов aij, равных
aij = DXi×DXj
aij = cov(Xi,Xj)
aij = M(Xi×Xj)
aij =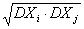 
pij - вероятности, определяющие закон распределения двумерной дискретной случайной величины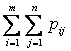 
равна ____ (ответ дайте числом)
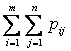равна ____ (ответ дайте числом)Ковариация cov(X,Y) случайных величин X и Y определяется как
cov(X,Y) = M(X – mx)×M(Y – my)
cov(X,Y) = M(X – mx) + M(Y – my)
cov(X,Y) = M[(X – mx) + (Y – my)]
cov(X,Y) = M[(X – mx)(Y – my)]
Вероятность появления успеха в каждом испытании равна 0,3. Тогда вероятность наступления 75 успехов при 200 испытаниях может быть определена при помощи
неравенства Чебышева
теоремы Пуассона
теоремы Маркова
теоремы Муавра-Лапласа
X и Y - две независимые случайные величины МХ = 1, DX = 3, МУ = 2, DY = 4 D(2Х + 3У) - ? Ответ дайте числом.
X и Y - две нормально распределённые случайные величины. X и Y некоррелированы. P{X < 1} = 0,3; P{Y < 2} = 0,4; P{X < 1; Y < 2} = ? Ответ дайте числом (десятичной дробью).
Функцией распределения двумерной случайной величины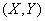 
называют функцию двух переменных F(x,y), равную
называют функцию двух переменных F(x,y), равнуюP{X < x }
P{X < x, Y < y}
P{Y < y / X < x}
P{X < x или Y < y}
Проводим 400 испытаний с вероятностью успеха в каждом испытании р = 0,5. S400 – число успехов. Ф(х) =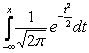 
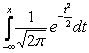
P{ S100 £ 220}
1 – Ф(2)
P{ S100 £ 200}
0,5
P{S100 ³ 220}
Ф(2)
X и Y - две случайные величины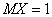 
, 
, 
, 
, 
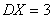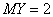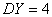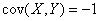D(Х + У) - ? Ответ дайте числом.
, , , , D(Х + У) - ? Ответ дайте числом.Неравенство Чебышева имеет вид
P{çX – MXú < a} £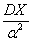 
P{çX – MXú ³ a} £ 1
P{çX – MXú ³ a} £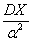
P{çX – MXú ³ a} ³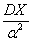
Пусть две независимые случайные величины X и Y имеют дисперсии DX = 2 и DY = 3, тогда D(X + Y) равна
1
2,5
6
5
Х и У некоррелированные нормально распределённые случайные величины. MX = 2, DX = 3;MY = 1, DY = 2
D(X + Y)
11
М(X + Y)
3
D(X – 2Y)
5
cov(X,Y) - ковариация случайных величин X и Y; Какие из утверждений верны?
cov(X,Y) = M(X – mx)×M(Y – my)
cov(X,Y) = M[(X – mx) + (Y – my)]
cov(X,Y) = M[(X – mx)(Y – my)]
cov(X,Y) = M(X×Y) – mx×m
F(x,y) - функция распределения двумерной случайной величины. Какие из утверждений верны
F(0,+¥) = 1
F(0,-¥) = 0
F(+¥, 0) = 1
F(-¥,0) = 0
Х - случайная величина, МХ = 2, DX = 3. По неравенству Чебышева P{çX – 2ú ³ 4} £ ? Ответ дайте дробью в виде a/b
Имеем однородную цепь Маркова с двумя состояниями H1 и Н2. Матрица переходных вероятностей (pij) =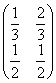 
. Р1 и Р2 - стационарные вероятности. Р2 - ? Ответ дайте в виде дроби a/b
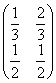. Р1 и Р2 - стационарные вероятности. Р2 - ? Ответ дайте в виде дроби a/bНекоррелированные случайные величины
всегда независимы
могут иметь коэффициент корреляции равным 0,5
могут быть линейно зависимы
могут быть зависимы
Берём 100 деталий. Вероятность детали быть бракованной равна 0,02. Х – число бракованных деталей.
P{ Х = 0}
×e-2P{ Х = 6}
×e-2P{ Х = 4}
e-2
Для однородного марковского процесса плотности вероятностей перехода lij
зависят от разности ti - tj (для любых моментов времени)
не зависят от t
обладают свойством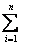 
lij = 1
lij = 1зависят от t
Независимые случайные величины X и Y имеют соответственно арактеристические функции gX(t) и gY(t), тогда характеристическая функция их суммы gX+Y(t) равна
gX(t) + gY(t)
gX(t) - gY(t)
gX(t)×gY(t)
gX(t):gY(t)
Если случайные величины X и Y связаны линейной зависимостью Y = -2X + 5, то коэффициент корреляции равен
0
+1
5
-1
X – случайная величина, имеющая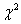 
-распределения с 3 степенями свободы. DХ - ? Ответ дайте числом
-распределения с 3 степенями свободы. DХ - ? Ответ дайте числомF(x,y) - функция распределения двумерной случайной величины (X,Y)
F(-¥,y)
неубывающая по у
F(¥,¥)
1
F(x,y)
0
Cлучайные величины X и Y независимы. Какие из утверждений всегда верны
D(X - Y) = DX - DY
M(X - Y) = 0
M(X - Y) = MX - MY
D(X - Y) = DX + DY
f(x,y) - плотность распределения непрерывной двумерной случайной величины. Какие из утверждений верны
f(0,-¥) = 0
f(0,0) = 1
f(-¥,0) = 0
f(0,+¥) = 1
X – случайная величина, имеющая 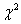-распределения с 4 степенями свободы. МХ - ? Ответ дайте числом
-распределения с 4 степенями свободы. МХ - ? Ответ дайте числомX и У независимые случайные величины. Чему равен коэффициент корреляции r(X,Y)? Ответ дайте числом.
Имеем однородную цепь Маркова с двумя состояниями H1 и Н2. Матрица переходных вероятностей (pij) =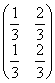 
. Р1 и Р2 - стационарные вероятности Какие из утверждений верны
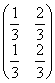. Р1 и Р2 - стационарные вероятности Какие из утверждений верныР1 =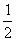 
Р2 =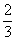 
Р1 =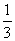 
Р2 =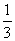
F(x,y) - функция распределения двумерной случайной величины. Какие из утверждений верны
F(0,-¥) = 0
F(+¥, +¥) = 1
F(-¥,0) = 0,5
F(0,+¥) = 1
Формула D(-X) = DX
верна, если Х может принимать только положительные значения
неверна
верна, если распределение Х – симметрично
верна всегда
F(x,y) - функция распределения двумерной случайной величины. Какие из утверждений верны
F(+¥, +¥) = 1
F(-¥,0) = 0
F(0,+¥) = 1
F(0,-¥) = 0,5
f(x,y) – плотность вероятности непрерывного случайного вектора (X,Y),
r(X,-2Х + 5)
Î [-1;1]
f(x,y)
Î [0;¥]
r(X,Y)
-1
X и Y - две случайные величины МХ = -1, МУ = 2. М(2Х + У) - ? Ответ дайте числом.
Пусть случайные величины Y и X связаны зависимостью Y = 5X, тогда коэффициент корреляции r(X,Y) равен
1
–1
5
0
Если случайные величины X и Y независимы, то дисперсия их разности D(X - Y) равна
0
1
DX + DY
DX – DY
Х - случайная величина, МХ = 2, DX = 3. По неравенству Чебышева P{çX – 2ú ³ 3} £ ? Ответ дайте дробью в виде a/b
Независимые случайные величины имеют распределение Пуассона с параметрами l1 = 0,5 и l2 = 1,5. Тогда сумма X + Y распределена по закону Пуассона с параметром l, равным
0,75
2
1
0,25
Случайные величины X и Y связаны линейной зависимостью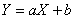 
; r(X,Y) – коэффициент корреляции случайных величин X и Y; Какие из утверждений верны?
; r(X,Y) – коэффициент корреляции случайных величин X и Y; Какие из утверждений верны?r(X, -5X + 5) = -1
r(X, 5X – 5) = 1
r(X, -5X + 5) = 1
r(X, 5X - 5) = 5
Х и У две независимые случайные величины распределённые по закону Пуассона с параметрами 3 и 4, Z = X + Y A) Пуассона с параметром l1 + l2 B) Пуассона с параметром l1 × l2 C) экспоненциальное с параметром l1 + l2 D) экспоненциальное с параметром l1 × l2
P{Z = 1}
7
P{Z = 0}
e-7
МZ
7×e-7
(aij) – ковариационная матрица случайного вектора (X1,X2, X3). X1,X2, X3 – независимы и имеют равные математические ожидания и дисперсии. MXi = 1, DXi = 2. a12 = ? Ответ дайте числом.
Если X1 и X2 независимые случайные величины, то характеристическая функция их суммы равна
MX = 2, DX = 3; MY = 1, DY = 2; cov(X,Y) = 1
D(X – Y)
5
D(X + Y)
7
М(2X + Y)
3
Случайная величина Х имеет 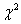-распределения с “n” степенями свободы Какие из утверждений всегда верны
-распределения с “n” степенями свободы Какие из утверждений всегда верныn – 1
n2
n
2n
Случайные величины X и Y называют независимыми, если функция распределения F(x,y) вектора (X,Y) может быть представлена в виде F(x,y) = FX(x) ? FY(y) Ответ дайте в виде x, +, – , :
Производство дает 1,5% брака. Тогда вероятность того, что из взятых на исследование 1000 изделий выбраковано будет не больше 15, может быть определена при помощи теоремы
Чебышева
Хинчина
Маркова
Муавра-Лапласа
Случайные величины X и У независимы f(x,y) – плотность вероятности непрерывного случайного вектора (X,Y), fX(x) и fY(y) – плотности вероятностей координат этого вектора
f(x,y)
DX + DY
M(X + Y)
MX + MY
D(X + Y)
fX(x)× fY(y)
F(x,y) – функция распределения двумерной случайной величины (Х,У); FX(x) – функция распределения случайной величины Х; FУ(x) – функция распределения случайной величины У; Х и У независимы Какие из утверждений верны
F(+¥,+¥) = 1
F(x,y) = FX(x) + FY(y)
F(x,y) = FX(x)×FY(y)
F(x,y) ≠ FX(x)×FY(y)