Математический анализ (курс 6)
Решением уравнения xUx - yUy - xy = 0 является функция
U = lnxy
U = lnx + yx
U = xy
U = xylnx
Даны два утверждения: 1) уравнение xUху - xyUz + xyz = 0 линейное неоднородное, 2) уравнение x2Ux - y2Uу + U2 = 0 линейное однородное. Утверждения
первое верно, второе неверно
первое неверно, второе верно
оба верны
оба неверны
Функция U является решением уравнения Utt = Uxx + sint×e-x. Тогда решением соответствующего однородного уравнения будет функция
U - sint×e-x
U + sint×e-x
U - 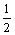 sint×e-x
sint×e-x
U + 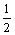 sint×e-x
sint×e-x
Функция U является решением уравнения Utt = Uxx + sint × cosx. Тогда решением этого же уравнения будет функция
U + 2xt
U + t2 - x2
U + x2t2
U + x2 - t2
Решением уравнения Uyy - Ux = 0 является функция
U = e-xcosy
U = e-ysinx
U = exsiny
U = eycosx
Функция у = sin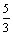 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 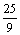 y = 0, y(0) = y(3) = 0
y = 0, y(0) = y(3) = 0
y¢¢ + 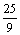 y = 0, y¢(0) = y(3p) = 0
y = 0, y¢(0) = y(3p) = 0
y¢¢ + 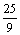 y = 0, y(0) = y(3p) = 0
y = 0, y(0) = y(3p) = 0
y¢¢ + 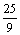 y = 0, y¢(0) = y(3) = 0
y = 0, y¢(0) = y(3) = 0
Функция U является решением уравнения Ut = Uxx + e-tcosx. Тогда решением этого же уравнения будет функция
U - etcosx
U + etsinx
U + etcosx
U - e-tcosx
Функция у = sin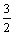 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 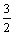 y = 0, y¢(0) = y(2p) = 0
y = 0, y¢(0) = y(2p) = 0
y¢¢ + 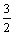 y = 0, y(0) = y(2p) = 0
y = 0, y(0) = y(2p) = 0
y¢¢ + 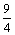 y = 0, y(0) = y(2p) = 0
y = 0, y(0) = y(2p) = 0
y¢¢ + 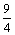 y = 0, y¢(0) = y(2p) = 0
y = 0, y¢(0) = y(2p) = 0
Гиперболический тип имеет уравнение
3Uxx + 2Uxy + Uyy = 0
3Uxx + 4Uyy = 0
3Uxy + 4Uyy = 0
Uxx + 2Uxy + Uyy = 0
Решение задачи y¢¢ +p2у = 0, у(0) = у(3) = 0 имеет вид
y = cospх
y = sin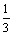 x
x
y = sinpх
y = sin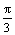 x
x
Решением уравнения Uxy = 0 является функция
U = (x -1)(y + 1)
U = x2y2
U = x2 + y2
U = xy
Волновое уравнение (одномерное) имеет вид
Ut = a2Ux
Utt = a2Ux
Utt = a2Uxx
Ut = a2Uxx
Область, в которой уравнение 2Uxx + yUхy - xUyy = 0 имеет гиперболический тип, расположена
внутри параболы у2 = - 8х
вне параболы у2 = 8х
вне параболы у2 = - 8х
внутри параболы у2 = 8х
Решением уравнения Ux - Uy - 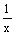 U = 0 является функция
U = 0 является функция
U = xsin(x + y)
U = xsin(x - y)
U = ysin(x - y)
U = ysin(x + y)
Уравнение теплопроводности на плоскости имеет вид
Ut= a2(Uxx + Uyy)
Utt = a2Uxx
Uxx = a2Uyy
Uxx - Ux = 0
Функция U является решением уравнения Ut = Uxx - etcosx. Тогда решением соответствующего однородного уравнения будет функция
U + 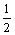 etsinx
etsinx
U - 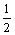 etsinx
etsinx
U + 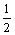 etcosx
etcosx
U - 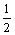 etcosx
etcosx
Даны два утверждения: 1) уравнение x2(Ux)2 - z2(Uy)2 + y2(Uz)2 = 0 линейное однородное, 2) уравнение y2Uxy - x2Uzx + z2Uzy = 0 линейное. Утверждения
оба неверны
первое верно, второе неверно
оба верны
первое неверно, второе верно
Даны два утверждения: 1) уравнение Uxx + х2Uy + zU = 0 имеет первый порядок, 2) уравнение y2Ux + xUy + (zUz)2 = 0 имеет первый порядок. Утверждения
оба неверны
первое верно, второе неверно
оба верны
первое неверно, второе верно
Решение задачи y¢¢ +9p2у = 0, у (0) = у¢(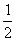 ) = 0 имеет вид
) = 0 имеет вид
y = sin3pх
y = cos3pх
y = cos3х
y = sin3х
Решением уравнения xUx + Uy - xU = 0 является функция
U = yex + y
U = xex + y
U = yex - y
U = xex - y
Решением уравнения Uxx + Uy = 0 является функция
U = e-xsiny
U = eycosx
U = e-ysinx
U = excosy
Функция у = cos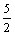 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 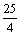 y = 0, y¢(0) = y¢(2p) = 0
y = 0, y¢(0) = y¢(2p) = 0
y¢¢ + 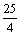 y = 0, y¢(0) = y(2) = 0
y = 0, y¢(0) = y(2) = 0
y¢¢ + 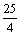 y = 0, y(0) = y(2p) = 0
y = 0, y(0) = y(2p) = 0
y¢¢ + 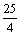 y = 0, y(0) = y¢(2p) = 0
y = 0, y(0) = y¢(2p) = 0
Решение задачи y¢¢ +16у = 0, у¢(0) = у¢(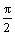 ) = 0 имеет вид
) = 0 имеет вид
y = cos4х
y = sin4pх
y = sin4х
y = cos4pх
Дифференциальное уравнение называется линейным, если
все независимые переменные входят в уравнение в первой степени
все неизвестные функции и их производные входят в уравнение в первой степени
все переменные входят в уравнение в первой степени
все неизвестные функции входят в уравнение в первой степени
Решение задачи y¢¢ +p2у = 0, у¢(0) = у(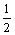 ) = 0 имеет вид
) = 0 имеет вид
y = cospх
y = sinpх
y = cos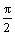 x
x
y = cosx
Функция у = cos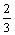 х является собственной функцией задачи Штурма-Лиувилля у¢¢ + lу = 0, у¢(0) = у¢(3p) = 0 с собственным значением
х является собственной функцией задачи Штурма-Лиувилля у¢¢ + lу = 0, у¢(0) = у¢(3p) = 0 с собственным значением
l = - 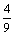
l = 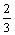
l = 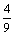
l = - 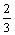
Даны два утверждения: 1) уравнение (Uxx)2 - (Uyy)2 + Uzz = 0 имеет второй порядок, 2) уравнение х2 (Ux) - у2 (Uy) - z3(Uz) = 0 имеет второй порядок. Утверждения
первое верно, второе неверно
первое неверно, второе верно
оба верны
оба неверны
Решение задачи y¢¢ +9у = 0, у(0) = у(p) = 0 имеет вид
y = cos3х
y = sin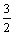 x
x
y = sin3pх
y = sin3х
Уравнение Uxx + 2yUxy + (x2 - 1)Uyy = 0 имеет гиперболический тип в области, расположенной
внутри гиперболы х2 - у2 = 1
вне гиперболы - х2 + у2 = 1
внутри гиперболы - х2 + у2 = 1
вне гиперболы х2 - у2 = 1
Решением уравнения Uxx - Uyy = 0 является функция
U = x2 - y2
U = 2x + 2y2
U = (x - y)2
U = x2 + 2y
Даны два утверждения: 1) уравнение у3Uху + x3Uуz - z3Uzz = U линейное неоднородное, 2) уравнение (Uzz)2 - x2(Uу)2 + y2(Ux)2 = 0 имеет второй порядок. Утверждения
оба верны
первое неверно, второе верно
оба неверны
первое верно, второе неверно
Гиперболический тип имеет уравнение
Uxx + Uyy = 0
5Uxx + 2Uxy - Uyy = 0
3Uxx + Uyy - Uxy = 0
4Uxx - 8Uxy + 4Uyy = 0
Даны два утверждения: 1) уравнение (х + y)2Uz - x2Uy + y2Ux = 0 имеет первый порядок, 2) уравнение (Uzz)2 - x2(Uy)2 + y2(Ux)2 = 0 имеет первый порядок. Утверждения
первое неверно, второе верно
первое верно, второе неверно
оба верны
оба неверны
Решением уравнения Ux - yUy - уU = 0 является функция
U = yex + y
U = yex - y
U = xex + y
U = xex - y
Решением уравнения Ux - Uy + 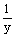 U = 0 является функция
U = 0 является функция
U = xsin(x - y)
U = ysin(x - y)
U = xsin(x + y)
U = ysin(x + y)
Уравнение 3Uxx + 2Uxy + 5Uyy = 0 имеет тип
смешанный
гиперболический
эллиптический
параболический
Даны два утверждения: 1) уравнение Uxх + уUy + U = 0 имеет второй порядок, 2) уравнение Uх + уUу + 4U = 0 линейное однородное первого порядка. Утверждения
оба неверны
первое верно, второе неверно
первое неверно, второе верно
оба верны
Функция у = cos5x является решением краевой задачи
y¢¢ + 25y = 0, y¢(0) = y(p) = 0
y¢¢ + 25y = 0, y¢(0) = y¢(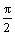 ) = 0
) = 0
y¢¢ + 25y = 0, y¢(0) = y¢(p) = 0
y¢¢ + 25y = 0, y¢(0) = y(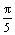 ) = 0
) = 0
Решение задачи y¢¢ +p2у = 0, у(0) = у¢(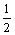 ) = 0 имеет вид
) = 0 имеет вид
y = cospх
y = sinpх
y = cosх
y = sinх
Функция U является решением уравнения Utt = Uxx + sinx + cost. Тогда решением этого же уравнения будет функция
U + x2 - t2
U - x2 + t2
U + x2 + t2
U - x2t2
Решением уравнения Ux + Uy - 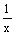 U = 0 является функция
U = 0 является функция
U = xsin(x + y)
U = xsin(x - y)
U = ysin(x + y)
U = ysin(x - y)
Решением уравнения Ux + Uy - 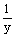 U = 0 является функция
U = 0 является функция
U = ysin(x - y)
U = ysin(x + y)
U = xsin(x + y)
U = xsin(x - y)
Функция U1 - решение линейного однородного уравнения LU = 0, функция U2 - решение неоднородного уравнения LU = ln(x+y). Тогда решением второго уравнения будет также функция
U2 - 3U1
3U1 - U2
3(U1 - U2)
3(U1 + U2)
Область, в которой уравнение 2Uxx - yUxy - xUyy = 0 имеет эллиптический тип, находится
внутри параболы у2 = -8х
вне параболы у2 = -8х
внутри параболы 8у = - х2
вне параболы 8у = - х2
Функция у = sin2px является решением краевой задачи
y¢¢ + 4p2y = 0, y(0) = y¢(1) = 0
y¢¢ + 4p2y = 0, y(0) = y(2) = 0
y¢¢ + 4y = 0, y(0) = y¢(1) = 0
y¢¢ + 4y = 0, y(0) = y(2) = 0
Область, в которой уравнение (y2 + 1)Uxx + xUxy + Uyy = 0 имеет эллиптический тип, находится
вне гиперболы 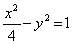
внутри гиперболы 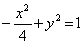
вне гиперболы 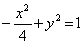
внутри гиперболы 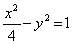
Функция U является решением уравнения Utt = Uxx + sinx + cost. Тогда решением соответствующего однородного уравнения будет функция
U + sinx - cost
U + sinx + cost
U - sinx + cost
U - sinx - cost
Функции U1 = x + y2 и U2 = e2xy являются решениями уравнения
Uxx + Uyy = 0
Uxx + Uyy - e-2xUy = 0
yUxx + Uyy - 2Ux = 0
Uxx + Uyy - 2Ux = 0
Уравнение Uxx - 4Uxy + 5Uyy = 0 имеет тип
параболический
гиперболический
смешанный
эллиптический
Функция у = cos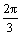 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 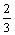 y = 0, y¢(0) = y¢(p) = 0
y = 0, y¢(0) = y¢(p) = 0
y¢¢ + 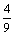 y = 0, y¢(0) = y¢(p) = 0
y = 0, y¢(0) = y¢(p) = 0
y¢¢ + 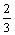 y = 0, y¢(0) = y¢(3p) = 0
y = 0, y¢(0) = y¢(3p) = 0