Математический анализ (курс 6)
Функция у = cos3pх является собственной функцией задачи Штурма-Лиувилля у¢¢ + lу = 0, у¢(0) = у¢(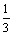 ) = 0 с собственным значением
) = 0 с собственным значением
l = 9
l = 9p2
l = 3p
l = 3
Функция f(x) = x2 разлагается в ряд Фурье 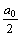 +
+ 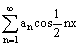 +
+ 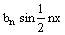 на отрезке [-2p, 2p]. Коэффициент a0 равен
на отрезке [-2p, 2p]. Коэффициент a0 равен
4p2
p2
0
Уравнение (x2 + 1)2Uxx + 2(x2 + 1)Uxy +Uyy = 0 имеет параболический тип
при всех у > х > 0
при всех х и у > 0
при всех (х, у), кроме (0, 0)
при всех (х, у)
Уравнение Uxx + xUxy - yUyy = 0 имеет эллиптический тип в области, расположенной
вне параболы у2 = - 4х
вне параболы у = - 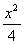
внутри параболы у = - 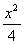
внутри параболы у2 = - 4х
Функция U1 - решение линейного неоднородного уравнения LU = x2 + y2, функция U2 - решение соответствующего линейного однородного уравнения. Тогда решением первого уравнения будет также функция
U2 - 4U1
4(U2 + U1)
U2 + 4U1
4U2 + U1
Даны два утверждения: 1) уравнение Uyy + Uzz + xU = y линейное неоднородное, 2) уравнение Ux - Uу + Uz = x2 имеет первый порядок. Утверждения
оба неверны
первое неверно, второе верно
оба верны
первое верно, второе неверно
Даны два утверждения: 1) уравнение (Uху)3 + (Uх)2 + (Uу)2 = 0 имеет второй порядок, 2) уравнение (x + y)2Uz - x2Uу + y2Ux = 0 линейное. Утверждения
оба неверны
оба верны
первое неверно, второе верно
первое верно, второе неверно
Функция f(x) = x разлагается в ряд Фурье 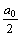 +
+ 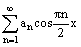 на отрезке [0, 2]. Коэффициент a0 равен
на отрезке [0, 2]. Коэффициент a0 равен
p
2
1
Функция U является решением уравнения Ut = Uxx + e-t + ex. Тогда решением соответствующего однородного уравнения будет функция
U - e-t + ex
U + e-t - ex
U + e-t + ex
U - e-t - ex
Уравнение Лапласа в пространстве имеет вид
Uxx + Uyy = Uzz
Uxx = Utt
Uxx + Uyy + Uzz = 0
Uxx + Uy = Utt
Даны два утверждения: 1) уравнение у2Ux + xUy + (zUz)2 = 0 линейное первого порядка, 2) уравнение (Uуу)2 + xUх - U2 = 0 линейное однородное второго порядка. Утверждения
оба неверны
оба верны
первое верно, второе неверно
первое неверно, второе верно
Функция U является решением уравнения Uxx + Uyy = sinx + siny. Тогда решением этого же уравнения будет функция
U + sinx + siny
U + x2 + y2
U + (х - y)2
U + x2 - y2
Функция U является решением уравнения Ut = Uxx + etx. Тогда решением этого же уравнения будет функция
U -2t + x2
U + 2tx2
U + 2t + x2
U - 2tx2
Функция U является решением уравнения Uxx + Uyy = cosx × cosy. Тогда решением этого же уравнения будет функция
U + 2xy
U + x2 + y2
U + 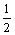 cosx × cosy
cosx × cosy
U - 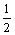 cosx × cosy
cosx × cosy
Функции U1 = e-ycosx и U2 = x2 + 2y + 5 являются решениями уравнения
Uyy - Uxx = 0
Uyy - Ux = 0
Uyy + Uxx = 0
Uxx - Uy = 0
Уравнение Uxx - 2yUxy + (1 - x2)Uyy = 0 имеет гиперболический тип в области, расположенной
вне окружности х2 + у2 = 4
вне окружности х2 + у2 = 1
внутри окружности х2 + у2 = 4
внутри окружности х2 + у2 = 1
Уравнение теплопроводности (одномерное) имеет вид
Utt + a2Uxx = 0
Utt = a2(Uxx + Uyy)
Utt = a2Uxx
Ut = a2Uxx
Уравнение Лапласа на плоскости имеет вид
Uxx = Uyy + Uzz
Ux = Uyy
Uxx = Uyy
Uxx + Uyy = 0
Уравнение 2Uxx - Uxy + Uyy = 0 имеет тип
гиперболический
параболический
смешанный
эллиптический
Даны два утверждения: 1) уравнение (Uz)2 - (Uy)2 + U2 = 0 нелинейное, 2) уравнение Uxx + Uуy + Uzz = U однородное. Утверждения
оба верны
оба неверны
первое неверно, второе верно
первое верно, второе неверно
Решение задачи y¢¢ +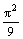 y = 0, y(0) = y(3) = 0 имеет вид
y = 0, y(0) = y(3) = 0 имеет вид
y = cos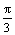 x
x
y = sin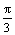 x
x
y = sin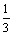 x
x
y = cos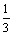 x
x
Функции U1 = 2xy + 5x - 3y и U2 = 5(x2 - y2) являются решениями уравнения
Ux + Uyy = 0
Uyy + U = 0
Uxx + Uyy = 0
Uxx - Uyy = 0
Уравнение уUxx + 2xUxy + Uyy = 0 имеет гиперболический тип в области, расположенной
внутри параболы у2 = х
внутри параболы у = х2
вне параболы у2 = х
вне параболы у = х2
Даны два утверждения: 1) уравнение yUxx + xUyy - z2Uzz = 0 линейное, 2) уравнение x2(Ux)2 - y2(Uy)2 - z3(Uz)2 = 0 имеет второй порядок. Утверждения
оба неверны
оба верны
первое неверно, второе верно
первое верно, второе неверно
Область, в которой уравнение xUxx - yUxy + Uyy = 0 имеет гиперболический тип, расположенна
внутри параболы у2 = - 4х
внутри параболы у2 = 4х
вне параболы у2 = - 4х
вне параболы у2 = 4х
Область, в которой уравнение (1 - x2)Uxx + yUxy + Uyy = 0 имеет эллиптический тип, находится
внутри эллипса х2 + 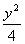 = 1
= 1
внутри эллипса 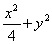 = 1
= 1
вне эллипса х2 + 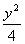 = 1
= 1
вне эллипса 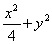 = 1
= 1
Решение задачи y¢¢ +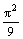 у = 0, у (0) = y¢(
у = 0, у (0) = y¢(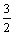 ) = 0 имеет вид
) = 0 имеет вид
y = cos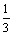 x
x
y = sin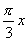
y = cos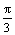 x
x
y = sin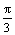 x
x
Эллиптический тип имеет уравнение
3Uxy + 4Uyy = 0
3Uxx - 2Uxy - Uyy = 0
4Uxx - 4Uxy + Uyy = 0
Uxx + 2Uxy + 3Uyy = 0
Параболический тип имеет уравнение
Uxx + 6Uxy - 9Uyy = 0
3Uxy - Uyy = 0
Uxx + Uxy = 0
Uxx + 6Uxy + 9Uyy = 0
Уравнение Uxx + xUxy + yUyy = 0 имеет эллиптический тип в области, расположенной
вне параболы у = 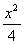
вне параболы у2 = 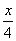
внутри параболы у2 = 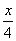
внутри параболы у = 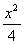
Даны два утверждения: 1) уравнение х2(Ux)2 - z2(Uy)2 + y2(Uz)2 = 0 имеет второй порядок, 2) уравнение (Uxx)2 + х2(Uyy)2 - y2(Uzz)2 = 0 имеет второй порядок. Утверждения
оба верны
первое неверно, второе верно
первое верно, второе неверно
оба неверны
Функция у = sin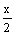 является решением краевой задачи
является решением краевой задачи
y¢¢ + 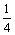 y = 0, y(0) = y¢(p) = 0
y = 0, y(0) = y¢(p) = 0
y¢¢ + 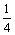 y = 0, y¢(0) = y¢(1) = 0
y = 0, y¢(0) = y¢(1) = 0
y¢¢ + 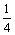 y = 0, y¢(0) = y¢(p) = 0
y = 0, y¢(0) = y¢(p) = 0
y¢¢ + 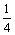 y = 0, y¢(0) = y(p) = 0
y = 0, y¢(0) = y(p) = 0
Функция у = sin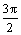 x является решением краевой задачи
x является решением краевой задачи
y¢¢ + 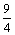 y = 0, y(0) = y(1) = 0
y = 0, y(0) = y(1) = 0
y¢¢ + 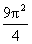 y = 0, y(0) = y¢(1) = 0
y = 0, y(0) = y¢(1) = 0
y¢¢ + 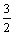 y = 0, y(0) = y(1) = 0
y = 0, y(0) = y(1) = 0
y¢¢ + 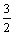 y = 0, y(0) = y¢(1) = 0
y = 0, y(0) = y¢(1) = 0
Уравнение 2Uxx - 4Uxy + 2Uyy = 0 имеет тип
смешанный
эллиптический
параболический
гиперболический
Эллиптический тип имеет уравнение
3Uxx - Uyy = 0
Uxx + 2Uxy + Uyy = 0
3Uxx + 4Uyy = 0
5Uxx + 2Uxy - Uyy = 0
Даны два утверждения: 1) уравнение y(Ux)2 + (Uy)2 - z(Uz)2 = 0 имеет второй порядок, 2) уравнение у3(Uxy) + х3(Uyz) - z3(Uzz) = 0 имеет первый порядок. Утверждения
оба неверны
первое неверно, второе верно
оба верны
первое верно, второе неверно
Область, в которой уравнение (y2 - 1)Uxx - 2xUxy + Uyy = 0 имеет эллиптический тип, находится
вне гиперболы х2 - у2 = 1
внутри гиперболы х2 - у2 = 1
внутри гиперболы -х2 + у2 = 1
вне гиперболы -х2 + у2 = 1
Уравнение (x + у)2Uxx + 2(xy + у2)Uxy +y2Uyy = 0 имеет параболический тип
при всех (х, у), кроме (0, 0)
при всех (х, у)
при всех х > -у > 0
при всех (х + у) > 0
Функция U является решением уравнения Ut = Uxx + et + ex. Тогда решением соответствующего однородного уравнения будет функция
U + et - ex
U - et + ex
U + et + ex
U - ex - et
Решением уравнения Ux - yUy + yU = 0 является функция
U = yex + y
U = yex - y
U = xex - y
U = xex + y
Уравнение 4Uxx + 8Uxy + 4Uyy = 0 имеет тип
гиперболический
эллиптический
смешанный
параболический
Уравнение уUxx + 2xUxy - Uyy = 0 имеет гиперболический тип в области, расположенной
внутри параболы у = - х2
внутри параболы у2 = -х
вне параболы у2 = -х
вне параболы у = - х2
Решением уравнения Uxx + Uyy = 0 является функция
U = x2 + y2
U = x2 - y2
U = x2y
U = x + y2
Эллиптический тип имеет уравнение
3Uxy + Uxy - Uyy = 0
Uxx - Uyy = 0
Uxx + Uyy = 0
4Uxx - 8Uxy + 4Uyy = 0
Функция U1 - решение линейного однородного уравнения LU = 0, функция U2 - решение неоднородного уравнения LU = sinx + y. Тогда решением второго уравнения будет также функция
U2 + 3U1
U1 - 3U2
3(U1 - U2)
3U2 + U1
Решение задачи y¢¢ +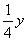 = 0, у(0) = у(4p) = 0 имеет вид
= 0, у(0) = у(4p) = 0 имеет вид
y = sin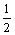 x
x
y = sin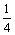 х
х
y = cos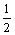 x
x
y = sin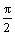 x
x
Уравнение 4Uxy - Uyy = 0 имеет тип
гиперболический
смешанный
эллиптический
параболический