Аналитическая геометрия и линейная алгебра
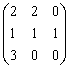
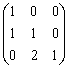
Матрица перехода от стандартного базиса в R3 к базису 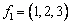 ,
, 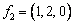 ,
, 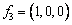 равна
равна
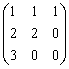
Уравнением z2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
пустое множество
координатную плоскость Oyz
точку
координатную плоскость Oxy
В треугольнике АВС стороны 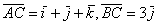 . Проекция
. Проекция 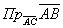 стороны
стороны 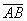 на сторону
на сторону 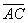 равна
равна
-3
3
0
1
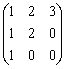
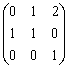
В пространстве многочленов степени 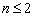 задан оператор дифференцирования
задан оператор дифференцирования 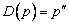 . Его матрица в базисе
. Его матрица в базисе 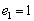 ,
, 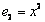 ,
, 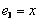 равна
равна
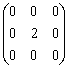
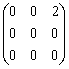
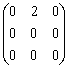
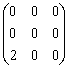
Частное от деления двух комплексно сопряженных чисел 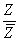 , где
, где 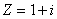 , равно
, равно
Из перечисленных прямых: 1) 2х-3у+1 = 0; 2) 6у-4х+2 = 0; 3) 3у = 4х-2; 4) 2х+3у-1=0; 5) 2х = 4+3у параллельными являются
1, 2, 4
1, 3, 5
1, 3, 4
1, 2, 5
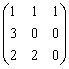
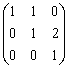
В пространстве многочленов степени 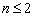 задан оператор дифференцирования
задан оператор дифференцирования 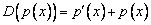 . Его матрица в базисе
. Его матрица в базисе 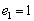 ,
, 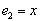 ,
, 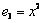 равна
равна
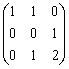
Метод аналитической геометрии был впервые сформулирован
Л.Эйлером
Р.Декартом
Г.Лейбницем
И.Ньютоном
Даны уравнения кривых второго порядка: 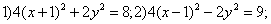

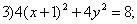
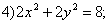 5)
5)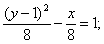
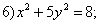 7)
7)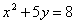 . Уравнениям эллипса (окружность - частный случай эллипса) в этом списке соответствуют уравнения
. Уравнениям эллипса (окружность - частный случай эллипса) в этом списке соответствуют уравнения
1, 2, 7
1, 3, 4, 6
2, 6, 7
1, 6
Через точки М1(-2,0,0), М2(2,0,2) и М3(2,2,0) проходит плоскость
х-2у-z+1=0
х-2у-2z+4=0
х-2у-2z+2=0
х-3у-2z+1=0
Общее решение системы 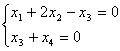 можно записать в виде
можно записать в виде
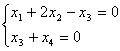 можно записать в виде
можно записать в виде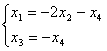 ;
; 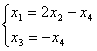 ;
; 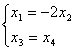 ;
; Уравнением x2 + y2 + z2 = -1 задается вырожденная поверхность второго порядка, представляющая собой
плоскость
прямую
точку
пустое множество
Уравнением первой степени относительно x, y называется уравнение вида
Ax + By + C = 0, A2 + B2 ¹ 0
Ax + By + C = 0, C ¹ 0
F(x, y) = 0
Ax + By + C = 0
На плоскости прямая х = 2
имеет угловой коэффициент k = -1
имеет угловой коэффициент k = 1
параллельна оси Ох
параллельна оси Оу
На плоскости прямая 2у = -5
имеет угловой коэффициент k = 2
параллельна оси Оу
параллельна оси Ох
имеет угловой коэффициент k = - 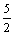
Координаты многочлена 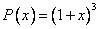 по базису
по базису 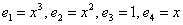 равны
равны
(1, 3, 1, 3)
(3, 3, 1, 1)
(1, 3, 3,1)
(1, 1, 3, 3)
Для системы уравнений 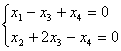 фундаментальной системой решений могут служить векторы
фундаментальной системой решений могут служить векторы
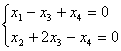 фундаментальной системой решений могут служить векторы
фундаментальной системой решений могут служить векторыПрямая 2х+2у-3 = 0 образует с положительным направлением оси ОХ угол, равный
0
Координаты многочлена 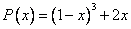 по стандартному базису
по стандартному базису 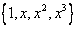 равны
равны
(1,-1, 3, -1)
(1, -2, 2, 0)
(1, 2, 1, 1)
(1, 2, 0, 0)
Среди векторов 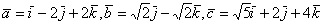 наибольшую длину имеет вектор
наибольшую длину имеет вектор
длины всех векторов равны
Даны два вектора 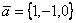 и
и 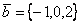 . Скалярный квадрат вектора
. Скалярный квадрат вектора 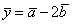 равен
равен
18
2
16
26
Данная поверхность 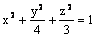 является
является
эллиптическим цилиндром
эллипсоидом
однополостным гиперболоидом
эллиптическим параболоидом
Даны два вектора 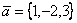 и
и 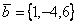 . Вектор
. Вектор 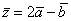 длиннее вектора
длиннее вектора 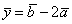 в k раз, где k равно
в k раз, где k равно
2
3
1
Объем параллелепипеда, построенного на векторах 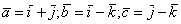 , равен
, равен
2
1
0
Фокусы эллипса имеют координаты 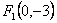 и
и 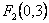 . Большая полуось равна 5. Уравнение эллипса имеет вид
. Большая полуось равна 5. Уравнение эллипса имеет вид
Расширенная матрица 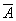 системы уравнений имеет вид:
системы уравнений имеет вид: 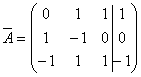 , тогда система
, тогда система
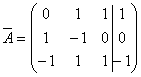 , тогда система
, тогда системаимеет единственное решение
имеет множество решений
несовместна
имеет три решения
Через точку (1, 1, 2) проходит
плоскость x + y + 2z = 0
прямая 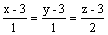
прямая 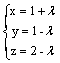
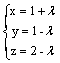
плоскость y + z + 2 = 0
В пространстве Oxyz уравнением плоскости по точке M0(x0, y0, z0) и нормальному вектору 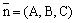 является уравнение
является уравнение
A(x - x0) + B(y - y0) + C (z - z0) = 0
Ax + By + Cz + D = 0
A(x - x0) + B(y - y0) + C (z - z0) + D = 0
Даны системы уравнений 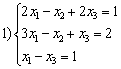 ,
, 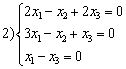 ,
, 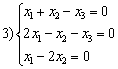 ,
, 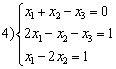 . Линейные подпространства образуют множества решений систем
. Линейные подпространства образуют множества решений систем
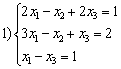 ,
, 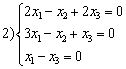 ,
, 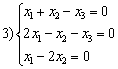 ,
, 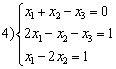 . Линейные подпространства образуют множества решений систем
. Линейные подпространства образуют множества решений систем2, 3
1, 2
3, 4
1, 4
Координаты фокуса параболы 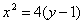 равны
равны
F (0; 1)
F (0; 2)
F (2; 0)
F (0; -1)
Уравнением x2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
пустое множество
координатную плоскость Oxz
точку
координатную плоскость Oyz
Вектор 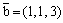
перпендикулярен прямой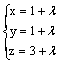
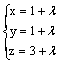
параллелен плоскости x + y + 3z -1 = 0
параллелен прямой 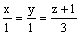
перпендикулярен плоскости 2(x - 1) + 4(y - 1) + (z - 3) = 0
К каноническому виду приведено следующее уравнение второго порядка
xy = 1
x2 + y2 + z2 + 2xz = 1
x2 - 5y2 + 6z2 = 30
x2 - 5y2 + 6z2 + x = 1
Даны два вектора 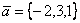 и
и 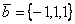 . Векторы
. Векторы 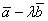 и
и 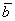 ортогональны, если число λ равно
ортогональны, если число λ равно
2
0
-2
Квадратичная форма 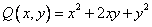 является
является
неотрицательно определенной
знаконеопределенной
положительно определенной
отрицательно определенной
Площадь треугольника АВС, где А(1,0,1), В(0,1,1), С(1,-1,1), равна
2 кв.ед.
1 кв.ед.
Базисом в пространстве 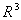 является система векторов
является система векторов
Квадратичная форма 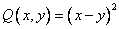 является
является
положительно определенной
знаконеопределенной
неотрицательно определенной
отрицательно определенной
В треугольнике АВС стороны 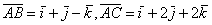 . Проекция
. Проекция 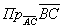 вектора
вектора 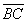 на вектор
на вектор 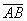 равна
равна
0
1
8
Каноническое уравнение прямой, проходящей через точку М0(1, -4) параллельно оси ОУ, имеет вид
у-4 = 0
х+1 = у-4
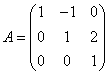 равны
равны