Аналитическая геометрия и линейная алгебра
Расширенная матрица 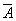 системы уравнений имеет вид:
системы уравнений имеет вид: 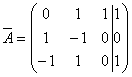 , тогда система
, тогда система
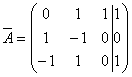 , тогда система
, тогда системаимеет множество решений
несовместна
имеет единственное решение 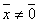
имеет лишь тривиальное решение
Квадратичная форма 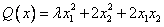 отрицательна определена при
отрицательна определена при 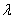
ни при каких 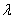
Даны две системы векторов 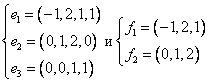 . Базис в R3 образуют системы
. Базис в R3 образуют системы
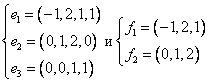 . Базис в R3 образуют системы
. Базис в R3 образуют системыникакая
обе
Данная поверхность 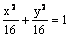 является
является
круговым цилиндром
конусом
эллипсоидом
гиперболическим цилиндром
Даны два вектора 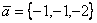 и
и 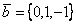 . Скалярный квадрат вектора
. Скалярный квадрат вектора 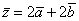 равен
равен
4
40
0
6
Даны два вектора 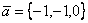 и
и 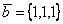 . Вектор (
. Вектор (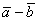 ) длиннее вектора (
) длиннее вектора (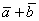 ) в k раз, где k равно
) в k раз, где k равно
5
3
2
1
Координаты функции 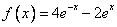 по базису
по базису 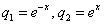 равны
равны
(-1, 2)
(-2, 4)
(2, -1)
(4, -2)
Векторы 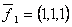 ,
, 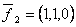 ,
, 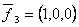 образуют базис в пространстве
образуют базис в пространстве 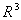 . Вектор
. Вектор 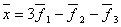 . Его координаты в базисе
. Его координаты в базисе 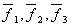 равны
равны
(3,-1,-1)
(1,2,3)
(1,0,1)
(1,1,3)
Даны векторы 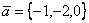 и
и 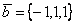 . Скалярное произведение векторов (
. Скалярное произведение векторов (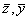 ), где
), где 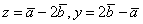 , равно
, равно
21
-20
20
-21
Если 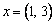 и
и 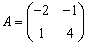 - матрица линейного преобразования А, то координаты образа
- матрица линейного преобразования А, то координаты образа 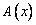 равны
равны
(-5, -11)
(1, 11)
(-5, 11)
(-5, 13)
На плоскости прямую, проходящую через точки М1(2, 0) и М2(0, -6), можно задать уравнением
х + у = 0
3(х -1) + 5(у + 2) = 0
у = 2х
Определитель Δ = 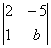 равен нулю при b, равном
равен нулю при b, равном
b = - 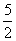
b = - 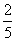
b = 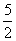
b = 0
Уравнение прямой , проходящей через точку (-2, 4) с нормальным вектором 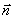 (1,3) имеет вид
(1,3) имеет вид
3(х+2)=у-4
х+2+3(у-4)=0
Если 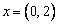 и
и 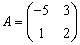 - матрица линейного преобразования А, то координаты образа
- матрица линейного преобразования А, то координаты образа 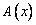 равны
равны
(0, 5)
(6, 4)
(0, 6)
(2, 4)
Вектор 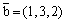 является
является
направляющим вектором прямой 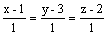
нормальным вектором плоскости 4(x - 1) + 5(y - 3) - 7(z - 2) = 0
направляющим вектором прямой 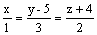
нормальным вектором плоскости x + 3y + 2 = 0
На плоскости прямая у = - 0,5х проходит через
начало координат
точку (2, -2)
точку (1, 0)
точку (0, -1)
Канонический вид имеет квадратичная форма
x2 + y2 + z2 + 3yz
4x2 - 5y2 + z2
x2 + y2 + z2 - 3yz
4x2 - 5y2 + z2 + 2xy - 2yz
Канонический вид имеет квадратичная форма
x2 - y2 - z2 - 2xz
2x2 + 5y2 + z2
3x2 - 2y2 + z2 + 2yz
x2 + y2 - z2 + 2xz +2yz
Уравнение линии 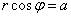 в декартовой системе имеет вид
в декартовой системе имеет вид
х+у = а
х-у = а
х =а
у = а
Объем параллелепипеда, построенного на векторах 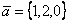 ,
, 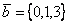 и
и 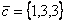 , равен
, равен
4 куб.ед.
0
1 куб.ед.
3 куб.ед.
На плоскости прямая х - у + 2 = 0 проходит через
точку (1, 1)
точку (0, 1)
начало координат
точку (-2, 0)
Из перечисленных прямых 1) у = 4х+1; 2) у = 2х-3; 3) у = - 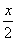 +4; 4) у= -4х-5 перпендикулярными являются
+4; 4) у= -4х-5 перпендикулярными являются
2 и 3
3 и 4
1 и 2
1 и 4
Даны два вектора 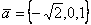 и
и 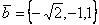 . Острый угол
. Острый угол 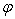 между этими векторами равен
между этими векторами равен
90°
30°
60°
45°
Произведение двух комплексно сопряженных чисел 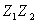 , где
, где 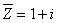 , равно
, равно
Система уравнений с матрицей 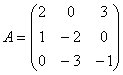 и вектором правых частей
и вектором правых частей 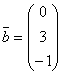 имеет вид
имеет вид
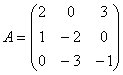 и вектором правых частей
и вектором правых частей 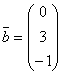 имеет вид
имеет вид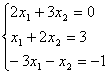
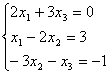
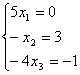
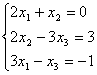
Среди формул для вычисления длины вектора 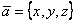 : 1)
: 1) 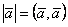 ; 2)
; 2) 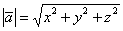 ; 3)
; 3) 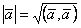 ; 4)
; 4) 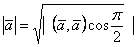 верными являются
верными являются
2, 3, 4
1, 3
2, 3
1, 2, 4
Координаты функции 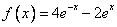 по базису
по базису 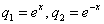 равны
равны
(-1, 2)
(4, -2)
(-2, 4)
(2, -1)
В пространстве Oxyz уравнение F(x, y, z) = 0 является уравнением данной поверхности, если
координаты (x, y, z) любой точки этой поверхности удовлетворяют этому уравнению
x2 + y2 + z2 ¹ 0
координаты любой точки (x, y, z) этой поверхности данному уравнению не удовлетворяют
координаты (x, y, z) каждой точки этой поверхности удовлетворяют этому уравнению, а координаты любой точки, не лежащей на поверхности, этому уравнению не удовлетворяют
Квадратичная форма 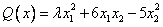 положительно определена при
положительно определена при 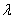
ни при каких 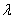
Координаты многочлена 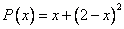 по стандартному базису
по стандартному базису 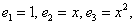 равны
равны
(-3, 1, 4)
(1, 2, 1)
(1, 4, 1)
(4, -3, 1)
Прямая 3х-3у+5 = 0 образует с положительным направлением оси ОХ угол, равный
0
Векторы 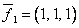 ,
, 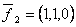 ,
, 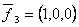 образуют базис в пространстве
образуют базис в пространстве 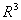 . Вектор
. Вектор 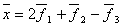 . Его координаты в стандартном базисе
. Его координаты в стандартном базисе 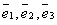 , где
, где 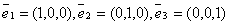 , равны
, равны
(2, 1, 1)
(2, 2, 2)
(2, 1, -1)
(2, 3, 2)
Заданы декартовы и полярные координаты точек А (2, 2), В (-2, 0), С (0, 2) и М (2, 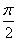 ), N(2,
), N(2, 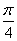 ), К (2,
), К (2, 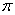 ). Из перечисленных точек совпадают следующие:
). Из перечисленных точек совпадают следующие:
В и К; С и М
А и N; В и К
А и К
С и К; В и М
Уравнение параболы с фокусом F(3, 0) и директрисой х+3 = 0 имеет вид
Данная поверхность 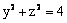 является
является
гиперболическим цилиндром
эллипсоидом
конусом
круговым цилиндром
Линейчатой поверхностью является
эллиптический параболоид
двухполостный гиперболоид
гиперболический параболоид
эллипсоид вращения
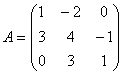 имеет вид
имеет вид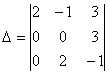 равен
равен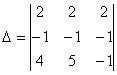 равен
равен