Аналитическая геометрия и линейная алгебра
Матрицы А и В равны соответственно А = 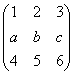 , В =
, В = 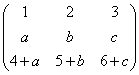 . Если det A = Δ, то det В равен
. Если det A = Δ, то det В равен
 , В =
, В = 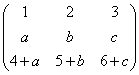 . Если det A = Δ, то det В равен
. Если det A = Δ, то det В равенΔ
0
2 Δ
15 Δ
Линейчатой поверхностью является
эллиптический параболоид
эллипсоид вращения
однополостный гиперболоид
двухполостный гиперболоид
Расширенная матрица 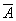 системы уравнений имеет вид:
системы уравнений имеет вид: 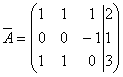 , тогда система
, тогда система
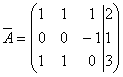 , тогда система
, тогда системанесовместна
имеет три решения
имеет множество решений
имеет единственное решение
В параллелограмме 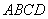 стороны
стороны 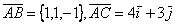 . Проекция
. Проекция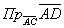 диаго-нали
диаго-нали 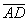 на сторону
на сторону 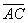 равна
равна
0
1
32
10
Данная поверхность 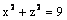 является
является
круговым цилиндром
эллипсоидом
конусом
гиперболическим цилиндром
На плоскости Oxy уравнение F(x, y) = 0 является уравнением данной линии, если
координаты (x, y) каждой точки, лежащей на линии, удовлетворяют этому уравнению, а координаты (x, y) каждой точки, не лежащей на линии, этому уравнению не удовлетворяют
координаты каждой точки, не лежащей на линии, не удовлетворяют этому уравнению
x2 + y2 ¹ 0
координаты (x, y) каждой точки, лежащей на линии, удовлетворяют этому уравнению
Расстояние от точки М(1, 1) до прямой 3х+4у+3 = 0 равно
10
2
3
1
Площадь треугольника АВС, где А(1,-1,2), В(2,1,0), С(1,0,1) равна
2 кв.ед.
1 кв.ед.
Определитель 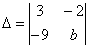 равен нулю при b равном
равен нулю при b равном
b = 6
b = - 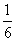
b = 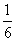
b = -6
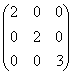
Матрица А равна А = 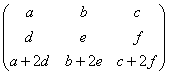 . Ее определитель det A равен
. Ее определитель det A равен
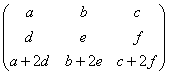 . Ее определитель det A равен
. Ее определитель det A равен2
8 det A
2 det A
0
Ранг квадратной матрицы А четвертого порядка r(A) = 3; ее определитель
Дано уравнение линии 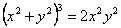 . В полярных координатах оно имеет вид
. В полярных координатах оно имеет вид
Квадратичная форма 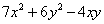 является
является
отрицательно определенной
неположительно определенной
неотрицательно определенной
положительно определенной
Данная поверхность 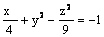 является
является
однополостным гиперболоидом
двухполостным гиперболоидом
гиперболическим цилиндром
эллипсоидом
Координаты многочлена 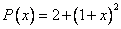 по базису
по базису 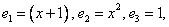 равны
равны
(1, 0, 1)
(2, 1, 1)
(1, 2, 0)
(1, 1, 1)
К каноническому виду приведено следующее уравнение второго порядка
x2 + y2 - z2 + 2xy = 1
z = xy
x2 + y2 + 4z2 = 8
x2 + y2 + 4z2 - x = 1
Матрицы А и В соответственно равны А = 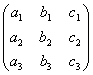 и В =
и В = 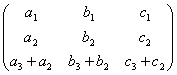 . Если det A = Δ, то det В равен
. Если det A = Δ, то det В равен
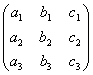 и В =
и В = 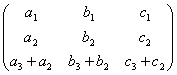 . Если det A = Δ, то det В равен
. Если det A = Δ, то det В равен3 Δ
0
Δ
2 Δ
Квадратичная форма 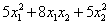 является
является
неположительно определенной
отрицательно определенной
положительно определенной
неотрицательно определенной
Уравнение прямой, проходящей через точки М1(1, 1) и М2(-5, -5), имеет вид
х-у+5 = 0
х-у = 0
х-5 = 5-у
х = -у
Даны две системы векторов: 1) 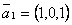 ,
, 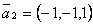 ,
, 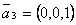 ; 2)
; 2) 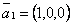 ,
, 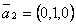 ,
, 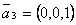 . Из них базисом в
. Из них базисом в 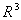 являются системы
являются системы
только 1
1 и 2
только 2
ни одна из них не является базисом
Даны декартовы координаты точки М (-1, 1). Ее полярные координаты
Число векторов базиса подпространства V решений системы уравнений 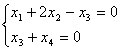 равно
равно
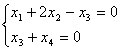 равно
равно1
2
3
4
Уравнение прямой, проходящей через точку (-1, 4) с нормальным вектором 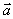 (2,3) имеет вид
(2,3) имеет вид
2(х+1)+3(у-4)=0
3(х+1)=2(у-4)
Даны две системы векторов 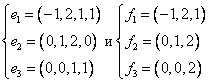 . Базис в R4 образуют системы
. Базис в R4 образуют системы
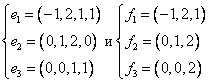 . Базис в R4 образуют системы
. Базис в R4 образуют системыобе
никакая
Координаты многочлена 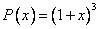 в стандартном базисе
в стандартном базисе 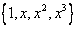 равны
равны
1, 1, 0, 0
1, 3, 3, 1
0, 0, 0, 1
3, 3, 1, 0
Координаты фокуса параболы 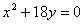 равны
равны
F (0; 4,5)
F (-4,5; 0)
F (4,5; 0)
F (0; -4,5)
Для матрицы А = 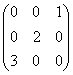 матрица, составленная из алгебраических дополнений, имеет вид
матрица, составленная из алгебраических дополнений, имеет вид
 матрица, составленная из алгебраических дополнений, имеет вид
матрица, составленная из алгебраических дополнений, имеет вид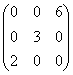
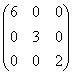

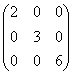
Из перечисленных прямых: 1) х = 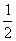 у; 2) 4х-2у+1 = 0; 3) 2х+у+12 = 0; 4) 2х-у+1=0; 5) у =
у; 2) 4х-2у+1 = 0; 3) 2х+у+12 = 0; 4) 2х-у+1=0; 5) у = 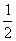 х параллельными являются
х параллельными являются
1, 4, 5
1, 4, 2
2 и 5, 3 и 5
1 и 4, 3 и 5
В пространстве многочленов степени 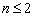 задан оператор дифференцирования
задан оператор дифференцирования 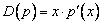 и функция
и функция 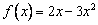 . Координаты образа
. Координаты образа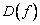 по базису
по базису 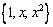 равны
равны
(2, -0, -6)
(2, -3, 0)
(2, -6, 0)
(0, 2, -6)
Среди множеств 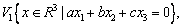
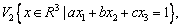
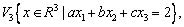
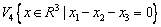 линейными подпространствами являются
линейными подпространствами являются
V1, V4
V2, V3
V1, V2
V3, V4
Расстояние d от точки М0(1, 1) до прямой 3х-4у+11 = 0 равно
d = 5
d = 2
d = 0
d = 1
Матрицы А и -2А равны, соответственно А =  , -2А =
, -2А = 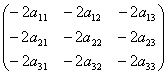 . Пусть det A = Δ, тогда det (-2A) равен
. Пусть det A = Δ, тогда det (-2A) равен
 , -2А =
, -2А = 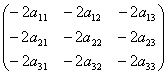 . Пусть det A = Δ, тогда det (-2A) равен
. Пусть det A = Δ, тогда det (-2A) равен- 8 Δ
2 Δ
8 Δ
- 6 Δ
Через точку (1, 2, 4) проходит
прямая 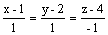
плоскость 4(x - 2) + 5(z - 1) = 0
прямая 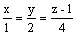
плоскость 2x + z = 0
Два вектора 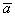 и
и 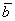 образуют базис на плоскости, если они
образуют базис на плоскости, если они
не компланарны
коллинеарны
параллельны этой плоскости и не коллинеарны
нулевые
Уравнением 2x2 + y2 + 4z2 + 3 = 0 задается вырожденная поверхность второго порядка, представляющая собой
прямую
плоскость
точку
пустое множество
Уравнением x2 + z2 = 0 задается вырожденная поверхность второго порядка, представляющая собой
точку
пустое множество
плоскость
прямую - ось ОУ
Дано уравнение эллипса 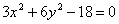 . Расстояния между вершинами эллипса равны
. Расстояния между вершинами эллипса равны
Через точку (3, 3, 0) проходит
прямая 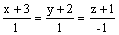
плоскость x + y + z - 6 = 0
прямая 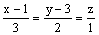
плоскость 3x + y + 5z + 13 = 0
Вектор 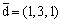 является
является
нормальным вектором плоскости x + 3y + 1 = 0
направляющим вектором прямой 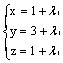
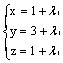
направляющим вектором прямой 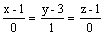
нормальным вектором плоскости 2x + 6y + 2z = 0
В пространстве многочленов степени 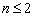 задан оператор дифференцирования
задан оператор дифференцирования 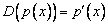 . Его матрица в базисе
. Его матрица в базисе 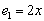 ,
, 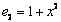 ,
, 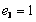 равна
равна
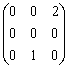
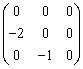
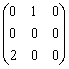
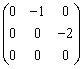
Данная поверхность 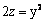 является
является
гиперболическим параболоидом
эллиптическим параболоидом
параболическим цилиндром
гиперболическим цилиндром
 равен
равен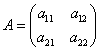 имеет вид
имеет вид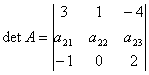 имеет вид
имеет вид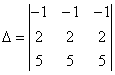 равен
равен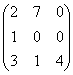
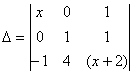 равен нулю при x равном
равен нулю при x равном