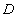Дифференциальное и интегральное исчисление функций нескольких переменных
Если кривая задана векторным уравнением 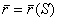 , где
, где 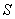 - длина дуги, то
- длина дуги, то 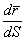 в некоторой точке - это
в некоторой точке - это
орт касательной, направленный в сторону возрастания 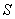
орт касательной
орт нормали
касательная прямая
Стационарная точка функции 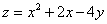
(0, 0)
не существует
(-2, 0)
(-1, 0)
Функция 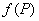 , заданная на множестве
, заданная на множестве 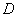 точек
точек 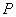 , непрерывна в точке
, непрерывна в точке 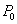 , если
, если
функция определена в точке 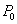
функция определена в точке 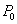 и ее
и ее 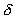 -окрестности
-окрестности
существуют 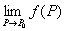 и
и 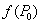
Двойной интеграл 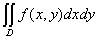 по области
по области 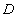 , ограниченной линиями
, ограниченной линиями 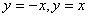 и
и 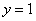 , равен повторному интегралу
, равен повторному интегралу
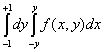
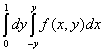
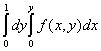
Достаточным признаком экстремума функции 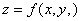 в точке
в точке 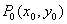 является
является
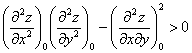
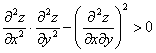
Областью определения функции 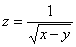 является множество
является множество
Производная 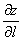 функции
функции 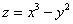 в точке
в точке 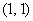 в направлении, задаваемом вектором
в направлении, задаваемом вектором 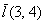 , равна
, равна
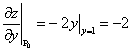 ,
, Производная 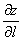 функции
функции 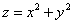 в направлении вектора
в направлении вектора 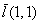 в точке
в точке 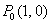 равна
равна
2
-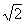
4
Градиент функции 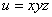 в точке
в точке 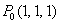 равен
равен
3
Двойной интеграл 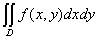 , где
, где 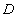 - область, ограниченная линиями
- область, ограниченная линиями 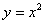 и
и 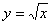 , равен повторному интегралу
, равен повторному интегралу
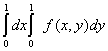
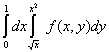
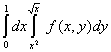
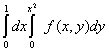
Наибольшая скорость возрастания функции 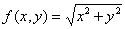 при переходе через точку (3, 4) равна
при переходе через точку (3, 4) равна
Кривая расположена в некоторой плоскости. Тогда соприкасающаяся плоскость к ней в какой-то ее точке есть
та плоскость, в которой расположена кривая
касательная плоскость
та плоскость, которая соприкасается с кривой
та плоскость, которая касается кривой
Областью определения функции 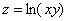 является множество
является множество
Параметрические уравнения кривой линии 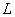 называются натуральными, если
называются натуральными, если
за параметр берется длина кривой
кривая - годограф векторной функции
за параметр принимается длина дуги 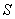 , отсчитываемая от некоторой зафиксированной точки до текущей по кривой точки
, отсчитываемая от некоторой зафиксированной точки до текущей по кривой точки 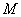
это векторное уравнение
Касательная плоскость к сфере 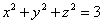 в точке
в точке 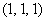 имеет уравнение
имеет уравнение
Градиент функции 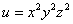 в точке (1,2,3) равен
в точке (1,2,3) равен
Функция 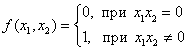 в точке (0, 0) имеет частные производные
в точке (0, 0) имеет частные производные 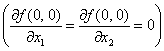 . Следовательно
. Следовательно
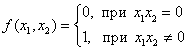 в точке (0, 0) имеет частные производные
в точке (0, 0) имеет частные производные 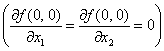 . Следовательно
. СледовательноОбластью определения функции 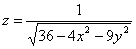 является множество
является множество
интервал с центром в этой точке
круг с центром в этой точке
шар с центром 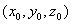 и радиуса
и радиуса 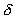 , причем поверхность сферы этого шара в
, причем поверхность сферы этого шара в 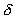 -окрестность не включается
-окрестность не включается
замкнутый шар радиуса 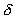
Двойной интеграл 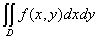 , где
, где 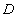 - область, ограниченная линиями
- область, ограниченная линиями 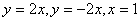 , равен повторному интегралу
, равен повторному интегралу
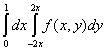
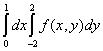
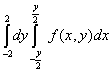
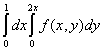
Дифференциалы 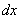 и
и 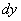 принимаются равными приращениям аргументов
принимаются равными приращениям аргументов 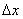 и
и 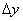 потому, что
потому, что
для функции 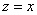 будет
будет 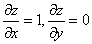 и
и 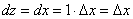 (для
(для 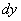 - аналогичное рассуждение)
- аналогичное рассуждение)
дифференциал 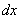 - главная часть приращения
- главная часть приращения 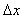
Частные производные функции 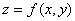 по
по 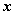 и
и 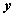 в точке
в точке 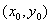 равны
равны
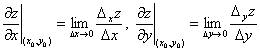
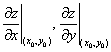
Частная производная 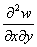 функции
функции 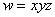 равна
равна
0
Полный дифференциал 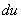 функции
функции 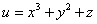 в точке
в точке 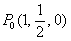 равен
равен
Областью определения функции 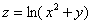 является множество
является множество
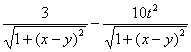
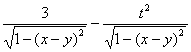
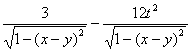
Областью определения функции 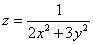 является
является
вся плоскость 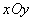 , кроме точки
, кроме точки 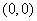
точка 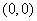
вся плоскость
Выражение 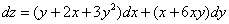 является
является
вторым дифференциалом
градиентом
неполным дифференциалом
полным дифференциалом
Градиент функции 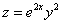 в точке
в точке 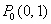 равен
равен
Двойным интегралом от функции 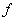 по области
по области 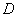 называется предел интегральных сумм _________ , где
называется предел интегральных сумм _________ , где 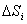 - площадь области
- площадь области 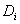 ,
, 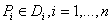
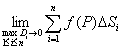
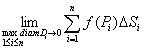
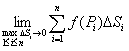
Точка 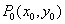 является граничной точкой множества
является граничной точкой множества 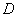 , если
, если
в некоторой 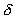 -окрестности
-окрестности 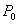 есть точки из
есть точки из 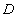 и точки, не принадлежащие
и точки, не принадлежащие 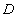
не принадлежит 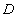
лежит на границе 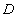
в любой 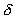 -окрестности
-окрестности 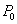 находятся как точки из
находятся как точки из 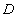 , так и точки, не принадлежащие
, так и точки, не принадлежащие 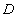
Если 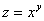 , то соответственно
, то соответственно 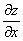 и
и 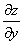 равны
равны
Областью определения функции 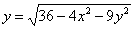 является множество
является множество
точек 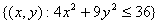
Градиент функции 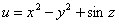 в произвольной точке равен
в произвольной точке равен
Пространство 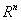 - это
- это
множество всевозможных упорядоченных наборов из 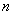 чисел (
чисел (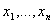 ), называемых точками этого пространства
), называемых точками этого пространства
множество точек
обобщение обычного пространства
вся плоскость
вся плоскость, кроме точки 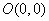
Кривизной 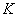 кривой линии в ее точке
кривой линии в ее точке 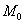 называется
называется
предел средней кривизны 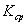 , когда
, когда 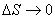 :
: 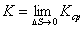
угол между касательными в точке 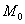
предел абсолютной величины угла между касательными при 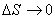
предел угла между касательными при 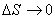
Полным дифференциалом функции 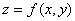 в точке
в точке 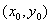 называется
называется
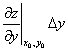
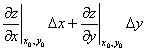
Если функция 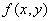 непрерывна в замкнутой ограниченной области
непрерывна в замкнутой ограниченной области 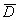 , дифференцируема во внутренних точках
, дифференцируема во внутренних точках 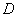 и имеет в
и имеет в 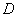 единственный экстремум - максимум, то своего наименьшего значения она достигает
единственный экстремум - максимум, то своего наименьшего значения она достигает
в граничной точке области
в другой точке внутри 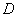
во внутренней или граничной точке
в любой точке
Стационарная точка функции 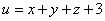
(-1, -1, -1)
не существует
(0, 0, 0)
(1, 2, -6)
Частная производная 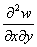 функции
функции 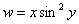 равна
равна
Известно, что в точке 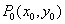 полное приращение
полное приращение 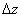 данной функции
данной функции 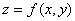 есть б.м. высшего порядка в сравнении с
есть б.м. высшего порядка в сравнении с 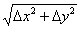 . Тогда дифференциал
. Тогда дифференциал 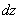 в этой точке
в этой точке
равен 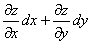
равен 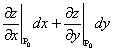
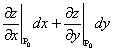
не определен
равен нулю
Полное приращение функции 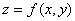 в точке
в точке 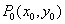 равно
равно
Стационарной точкой функции 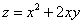 будет
будет
(2, -1)
(0, 0)
(1, -1)
Двойной интеграл 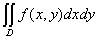 , где
, где 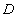 - область, ограниченная линиями
- область, ограниченная линиями 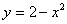 и
и 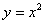 , равен повторному интегралу
, равен повторному интегралу
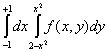
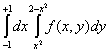
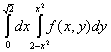
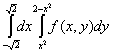
Неявная функция задана уравнением 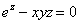 . Тогда частные производные
. Тогда частные производные 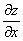 и
и 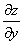 соответственно раны
соответственно раны
Наибольшая скорость возрастания функции 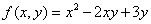 при переходе через точку (1, 2) равна
при переходе через точку (1, 2) равна
1
Производная 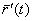 векторной функции
векторной функции 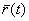 при
при 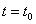 направлена по
направлена по
касательной прямой в точке 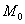
нормали к линии
касательной прямой к годографу функции 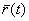 , проведенной в точке
, проведенной в точке 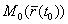
касательной прямой
Замкнутая область 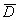 - это
- это
множество, ограниченное поверхностью
множество, получающееся, если к открытой области 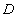 присоединить все ее граничные точки
присоединить все ее граничные точки
замкнутый интервал
множество всех граничных точек