Основы математической обработки информации
Сколько существует точек экстремума функции, если на рисунке изображен график ее производной: 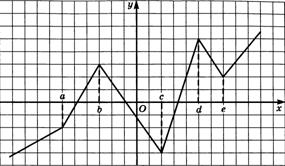

3
6
5
1
Имеет ли заданная функция точки разрыва, и если имеет, определите их. 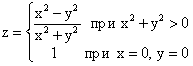
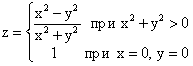
(-1;1)
(0;0)
(1;-1)
не имеет
Верны ли утверждения: А) Если события А и В несовместны, то для них справедливо равенство Р(А + В) = Р(А) + Р(В); В) Вероятность суммы двух случайных событий вычисляется по формуле Р(А + В) = Р(А) + Р(В)
А –да, В – нет
А –нет, В – да
А –нет, В – нет
А – да, В – да
Если связь между признаками отсутствует, то парный коэффициент корреляции равен
-1
0,1
1
0
Если известна вероятность события А, равная Р(А), то вероятность противоположного события Р(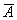 ) определяется как
) определяется как
1 - Р(А)
Р(А) - 1
0
Р(А)
Чему равна производная функции в точке x = 3? 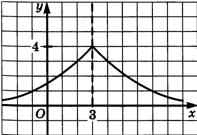

3
1
Не существует
0
График функции имеет асимптоты, если
lim f(x) = b и f(x) = 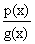 , а при х = m знаменатель обращается в нуль, а числитель отличен от нуля
, а при х = m знаменатель обращается в нуль, а числитель отличен от нуля
всегда
lim f(x) = b
f(x) = 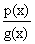 и при х = m знаменатель обращается в нуль, а числитель отличен от нуля
и при х = m знаменатель обращается в нуль, а числитель отличен от нуля
Дисперсию случайной величины Y = a X + b, которая является линейной функцией от случайной величины Х, вычисляют как
DY = a2 DX+b
DY = a DX
DY = a2 DX
DY = (a2 – b)DX
Определите точки экстремума функции 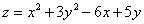 и его характер
и его характер
единственная точка 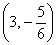 – максимум
– максимум
единственная точка 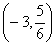 – минимум
– минимум
единственная точка 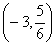 – максимум
– максимум
единственная точка 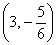 – минимум
– минимум
Уравнение регрессии Y на Х, выраженное через коэффициент корреляции, имеет вид
Прямые эмпирической регрессии параллельны, если
коэффициент корреляции равен -1 и они слились в одну
модуль коэффициента корреляции равен 1 и они слились в одну
они слились в одну
коэффициент корреляции равен 1
Функция у = f(x) непрерывна в точке х = а, если в этой точке выполняется следующее условие
если ∆х → 0, то∆ у= 0
если ∆х → 0, то∆ у→ 1
если ∆х → 0, то∆ у→ 0
Найдите наибольшее и наименьшее значение функции y =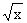 на промежутке [0;9]
на промежутке [0;9]
yнаим = 0 yнаиб =3
yнаим = -3 yнаиб =0
yнаим = 0 yнаиб =2
yнаим = 1 yнаиб =3
Верно ли, что: А) Одним из распространенных методов многомерного шкалирования является процедура попарного сравнения. В) При применении метода шкалирования не возможно предварительное ранжирование объектов.
А – да, В – нет
А – нет, В – да
А – нет, В – нет
А – да, В – да
Для выделения существенных для того или иного процесса факторов и их ранжирования используются:
методы попарного сравнения
вторичного шкалирования
методы экспертных оценок
метод регрессионного анализа
Функция распределения непрерывной случайной величины F(x) выражается через ее плотность распределения f(x) следующим образом
F(x) = 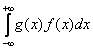
F(x) = 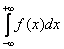
F(x) =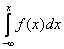
F(x) = 
Статистика, с помощью которой по эмпирическому значению коэффициента корреляции r и числу испытаний n проверяется значимость коэффициента корреляции, вычисляется по формуле:
Для функции f(x)= - 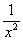 найдите хотя бы одну первообразную.
найдите хотя бы одну первообразную.
-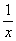
Отношение приращения функции y = 2x2 к приращению аргумента в точке x = 4 равно:
4+Δx
16+Δx
16
8+ Δx
Определите, в каких точках функция имеет экстремум, если на числовой прямой изображены точки, в которых производная функции равна нулю и даны знаки производной на интервалах. 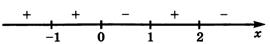
-1, 0, 1, 2
0, 2
-1, 0, 1
0, 1, 2
Вычислите площадь фигуры, ограниченной линиями х = 2, у = 1+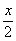 , у = ех
, у = ех
е-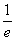
Связь между определенным интегралом и первообразной задается соотношением
v(t)dt = s(dt)
Двойной интеграл 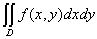 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 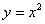 и
и 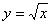 , равен повторному интегралу
, равен повторному интегралу
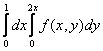
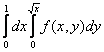
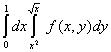
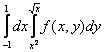
Определите скорость изменения функции f(x) = x2 в точке x = 2
8
1
4
2
Если 0 < а < 1, то последовательность уn = аn
стационарная
возрастает
не монохромная
убывает
Геометрический смысл определенного интеграла -
скорость движения материальной точки
перемещение точки, движущейся по прямой со скоростью v = v(t), за промежуток времени от t = а до t =b
площадь криволинейной трапеции
масса прямолинейного неоднородного стержня с плотностью р(x)
Определите промежутки монотонности функции y = x2-x
x≥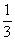 функция возрастает, x≤
функция возрастает, x≤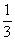 функция убывает
функция убывает
x≥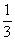 функция убывает, x≤
функция убывает, x≤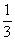 функция возрастает
функция возрастает
x≥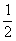 функция возрастает, x≤
функция возрастает, x≤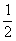 функция убывает
функция убывает
x≥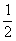 функция убывает, x≤
функция убывает, x≤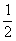 функция возрастает
функция возрастает
Вариация – это
среднеквадратичное отклонение
изменение значений признака во времени и/или в пространстве
отклонение средней арифметической абсолютных значений отдельных вариантов от их средней арифметической
разность между максимальным и минимальным значениями признака
Найдите угловой коэффициент касательной к графику функции y =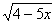 в точке а = 0
в точке а = 0
-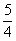
-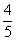
Тангенс угла между линиями регрессии через их коэффициенты регрессии ayx и axy вычисляется по формуле
Особенность методов вторичного шкалирования состоит в
использовании методов экспертных оценок
использовании метода временных рядов
использовании метода регрессионного анализа
построении матрицы взаимосвязей
Верно ли, что: А) Средняя ошибка выборки не зависит от объема выборки. В) Для уравнения линейной парной регрессии 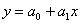 условие
условие 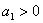 означает, что с увеличением x величина y увеличивается.
означает, что с увеличением x величина y увеличивается.
А – да, В – да
А – да, В – нет
А – нет, В – да
А – нет, В – нет
Линейный коэффициент корреляции r определяется по формуле
Найти эмпирический коэффициент корреляции между весом и ростом для выборки: 
1
0,5
0,8
-1
Укажите точки, в которых производная равна нулю или не существует 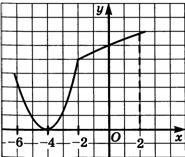

y′=0 при x= -4, y′ не существует при x= -2
y′=0 при x= -4, существует при всех значениях x
y′≠0 при всех значениях x,y′ не существует при x= -2
y′=0 при x= -2, y′ не существует при x= -4
Случайная величина Х распределена равномерно на [1;9], тогда вероятность попасть в интервал [4;5] равна
Случайная величина Х распределена по нормальному закону. Известно, что математическое ожидание и среднеквадратическое отклонение этой случайной величины соответственно равны 30 и 10. Плотность распределения Х имеет вид
Верно ли, что: А) Гипотезы об однородности выборок – это гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности. В) Для оценки тесноты связи между признаками (Х,Y) в числовой форме вычисляют коэффициент корреляции - безразмерную характеристику, выражающую тесноту связи между признаками в числовой форме.
А – нет, В – да
А – нет, В – нет
А – да, В – да
А – да, В – нет
Уравнение регрессии Y на Х, выраженное через коэффициент корреляции, имеет вид
Верно ли, что: А) Шкалирование может выступать либо как сравнение и числовая оценка сравнительных суждений, либо как прямая числовая оценка субъективных впечатлений по заданной шкале. В) При применении метода шкалирования экспериментатором на основе уже имеющихся теоретических или(и) эмпирических данных определяется и конструируется определенная шкала измерения.
А – нет, В – да
А – да, В – нет
А – да, В – да
А – нет, В – нет
Верны ли утверждения: А) Если из условия х1≠х2 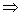 у1≠у2 (х1,х2
у1≠у2 (х1,х2 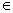 А; у1,у2
А; у1,у2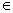 В, то отображение множеств А
В, то отображение множеств А 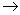 В необратимою В) Между эквивалентными множествами всегда можно установить взаимно-однозначное соответствие.
В необратимою В) Между эквивалентными множествами всегда можно установить взаимно-однозначное соответствие.
А – да, В – нет
А – да, В – да
А – нет, В – нет
А – нет, В – да
Для функции f(x) = х2+х16 найдите хотя бы одну первообразную.
3 х3+17 х17
х3+х17
Угол между касательной к графику функции f(x) и положительным направлением оси x составляет 60о. Найти f ′(x)
-1
1
Доля выборки вычисляется по формуле (n – объем выборки, N – объем генеральной совокупности)
В урне находятся 5 белых, 4 зеленых и 3 красных шара. Наугад извлекается один шар. Вероятность того, что он будет цветным, равна
Верно ли, что: А) Метод многомерного шкалирования - система методических приемов и способов сбора и обработки информации для получения объективных данных о закономерностях поведения одномерных объектов. В) Основанием для многомерного шкалирования является наличие определенной зависимости между оценками сходства и различия объектов, полученных от респондентов.
А – да, В – нет
А – нет, В – да
А – нет, В – нет
А – да, В – да
Если величина линейного коэффициента корреляции равна 1, то характер связи:
функциональный
устойчивый
слабый
средний
Имеет ли функция y = f(x) предел при x → -6, и чему он равен, если y=-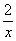
-6
-2
Не имеет