Функциональные соответствия и отношения. Алгебраические операции. Булевы функции. Предикаты
Выражение булевой функции X ÚY полиномом Жегалкина (через Å, &, 1)
X Y Å X Å Y
X Å Y Å 1
X Y Å 1
X Y Å X Å Y Å 1
Укажите свободные и связанные переменные в кванторных формулах
$Z"X,Y P(X, Y, Z)
X – связанная, Y, Z - свободные
"Z $Y P(X, Y, Z)
Y, Z – связанные, X - свободная
"X P(X, Y, Z)
X, Y, Z – связанные
Число элементарных конъюнкций в СДНФ функции 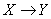 равно
равно
2
1
3
4
Укажите функции, соответствующие суперпозициям одноместной функции f(X) = sinX и двуместной функции g(X, Y) = X – Y
g(f(Y), X)
X – sinY
f(g(Y, X))
Sin(Y-X)
g(X, f(Y))
SinY – X
Бинарное отношение «правее» между точками на числовой прямой является
симметричным
транзитивным
нетранзитивным
антисимметричным
Булевы функции 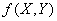 и
и 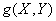 задаются столбцами значений
задаются столбцами значений 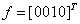 и
и 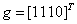 . Столбцом значений функции
. Столбцом значений функции 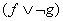 является [ _ ]T.
является [ _ ]T.
Тождество ¬(X Ú Y) = ¬X & ¬Y называется законом
тождества
де Моргана
Поста
исключенного третьего
Числовое множество 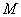 задается порождающей процедурой: (1) 4 Î М; (2) если
задается порождающей процедурой: (1) 4 Î М; (2) если 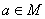 , то
, то 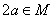 ; (3) если
; (3) если 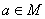 , то
, то 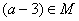 . Элемент
. Элемент 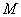 , определяемый последовательностью операций (2) à (3) à (3) à (2), равен ____ (ответ – целое число).
, определяемый последовательностью операций (2) à (3) à (3) à (2), равен ____ (ответ – целое число).
Бинарное отношение R(x, y) есть отношение строгого порядка, если оно
транзитивно, антисимметрично и рефлексивно
рефлексивно, симметрично и транзитивно
транзитивно, антисимметрично и антирефлексивно
транзитивно и антисимметрично
Тождество (X ÅY) & Z = (X & Z) Å (Y & Z) означает, что
(X & Z) ~ (Y & Z)
операция & дистрибутивна относительно операции Å
операция Å дистрибутивна относительно операции &
(X ÅY) ~ Z
Булевы функции 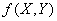 и
и 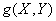 задаются столбцами значений
задаются столбцами значений 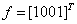 и
и 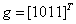 . Столбцом значений функции
. Столбцом значений функции 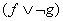 является [ _ ]T.
является [ _ ]T.
Числовое множество 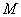 задается порождающей процедурой: (1)
задается порождающей процедурой: (1) 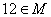 ; (2) если
; (2) если 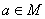 , то
, то 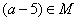 ; (3) если
; (3) если 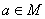 , то
, то 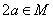 . Элемент
. Элемент 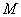 , определяемый последовательностью операций (2) à (3) à (2) à (3), равен ____ (ответ – целое число).
, определяемый последовательностью операций (2) à (3) à (2) à (3), равен ____ (ответ – целое число).
Подстановка константы 1 вместо 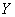 превращает функцию
превращает функцию 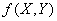 в
в
логическую константу
1
Арифметическая операция умножения чисел X • Y является
некоммутативной
коммутативной
неассоциативной
ассоциативной
СДНФ булевой функции, задаваемой таблицей 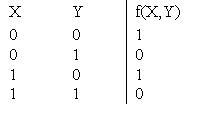 содержит элементарную конъюнкцию
содержит элементарную конъюнкцию
 содержит элементарную конъюнкцию
содержит элементарную конъюнкциюX Y
X 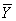
Сопоставьте свойства операций сложения и умножения с тождествами, выражающими эти свойства:
(X + Y) • Z = X • Y + X • Z
Коммутативность
(X + Y) + Z = X + (Y + Z)
Ассоциативность
X + Y = Y + X
Дистрибутивность умножения относительно сложения
Число элементарных конъюнкций в СДНФ функции X & Y равно
1
2
4
3
Для множеств 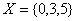 и
и 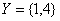 предикат
предикат 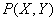 : "
: "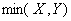 – четное число" может быть представлен таблицей
– четное число" может быть представлен таблицей
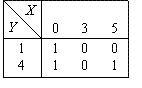
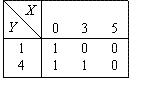
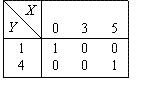
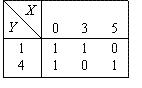
Алфавитное упорядочение слов ЛОШАДЬ, ЛИНЗА, ЛОМОТЬ, ЛОМ
2, 4, 3, 1
1, 2, 4, 3
3, 2, 1, 4
3, 4, 1, 2
Сопоставьте наименования свойств бинарного отношения xRy с их определениями:
Симметричность
"x, y, z: (xRy & yRz) à xRz
Рефлексивность
"X: xRx
Транзитивность
"x,y: xRy à yRx
Булевы функции 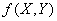 и
и 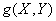 задаются столбцами значений
задаются столбцами значений 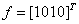 и
и 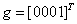 . Столбцом значений функции
. Столбцом значений функции 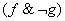 является [ _ ]T.
является [ _ ]T.
Число элементарных конъюнкций в СДНФ функции f(X, Y, Z), заданной столбцом значений 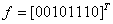 , равно
, равно
8
3
может быть различным
4
Предикатная формула 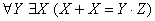 представляет собой
представляет собой
двуместный предикат P(X, Y)
трехместный предикат P(X, Y, Z)
высказывание
одноместный предикат P(Z)
Функция, заданная на трехмерном единичном кубе 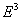 ,
, 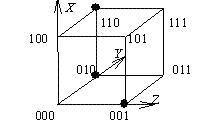 имеет СДНФ
имеет СДНФ
 имеет СДНФ
имеет СДНФТождество (X & Y) Ú Z = (X Ú Z)& (Y Ú Z) означает, что
(X Ú Y) ~ Z
(X Ú Z) ~ (Y Ú Z)
операция Ú дистрибутивна относительно операции &
операция & дистрибутивна относительно операции Ú
Булева функция, задаваемая таблицей 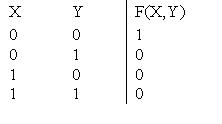 выражается формулой
выражается формулой
 выражается формулой
выражается формулойX & Y
X & ¬Y
¬X & Y
¬X & ¬Y
Декартовым произведением 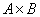 множеств A={1, 4, 6} и B={3, 4} является
множеств A={1, 4, 6} и B={3, 4} является
{1 • 4 • 6 • 3 • 4}
{3, 4, 12, 16, 18, 24}
{(1, 3), (1, 4), (4, 3), (4, 4), (6, 3), (6, 4)}
Предикатная формула 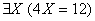 на предметной области натуральных чисел
на предметной области натуральных чисел  представляет собой
представляет собой
линейное уравнение
ложное высказывание
истинное высказывание
одноместный предикат
На координатной плоскости изображено декартово произведение 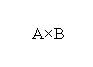 множеств (отрезков) А = [2, 6] и B = [1, 4].
множеств (отрезков) А = [2, 6] и B = [1, 4]. 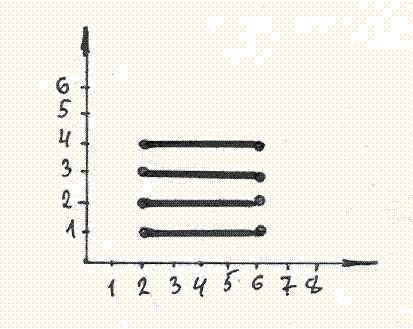
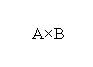 множеств (отрезков) А = [2, 6] и B = [1, 4].
множеств (отрезков) А = [2, 6] и B = [1, 4]. 
А и B – множества целых чисел
A и В – множества действительных чисел
A - множество целых чисел, В - множество действительных чисел
А - множество действительных чисел, В - множество целых чисел
Подстановка значений Х = 0 и Х = 1 показывает, что булева функция 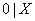 тождественно равна функции
тождественно равна функции
0
1
X
Переменные в предикатной формуле 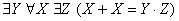 :
:
X, Y – свободные, Z - связанная
X, Y – связанные, Z - свободная
X, Y, Z - связанные
X, Y, Z – свободные
Число элементарных конъюнкций в СДНФ функции 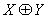 равно
равно
1
4
3
2
Декартовым произведением 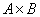 множеств A={3,4} и B={4,5,6}является
множеств A={3,4} и B={4,5,6}является
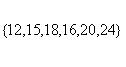
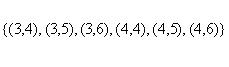
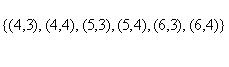
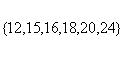
Обозначим через Ц(S, T) бинарное отношение между квадратами на плоскости: два квадрата S и T находятся в отношении Ц(S, T), если их центры совпадают. Отношение Ц(S, T)
несимметрично
нетранзитивно
симметрично
транзитивно
Булевы функции 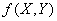 и
и 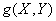 задаются столбцами значений
задаются столбцами значений 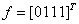 и
и 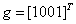 . Столбцом значений функции
. Столбцом значений функции 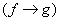 является
является
Схема из трех функциональных элементов 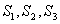 ,
, 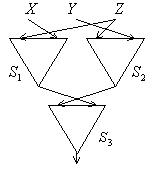 где
где 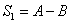 ,
, 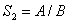 ,
, 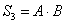 , реализует функцию
, реализует функцию
 где
где Булева функция, задаваемая таблицей 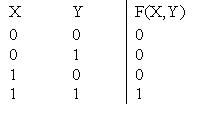 называется
называется
 называется
называетсядизъюнкцией
суммой по модулю 2
конъюнкцией
импликацией
1
0, если X ≠ Y
1, если X ≠ Y
зависит от знаков чисел X, Y
При алфавитном упорядочении перестановок чисел 1, 2, 3, 4 непосредственно следующей за 2 4 3 1 является
2 1 3 4
3 1 2 4
3 1 4 2
3 2 1 4