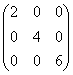
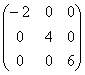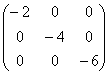Линейная алгебра. Часть 1
Матрица, определитель которой отличен от нуля, называется _________ матрицей (вставить слово)
Общее решение системы уравнений 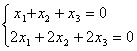 имеет вид:
имеет вид:
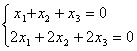 имеет вид:
имеет вид:
система имеет единственное решение (0, 0, 0)
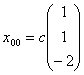 , где с – константа
, где с – константаСистема уравнений 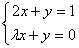 имеет единственное решение при значении
имеет единственное решение при значении 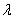 :
:
система несовместна при любом 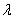
система имеет множество решений при любом 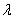
Если система уравнений 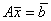 , где А – квадратная матрица может быть решена методом Крамера, то матрица А _______ (вставить слово)
, где А – квадратная матрица может быть решена методом Крамера, то матрица А _______ (вставить слово)
Ранг диагональной матрицы равен _________ ненулевых элементов ее главной диагонали (слово)
Чтобы для квадратной матрицы 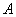 существовала обратная матрица
существовала обратная матрица 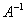 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 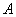 была _________ матрицей (вставить слово)
была _________ матрицей (вставить слово)
Неоднородная система уравнений 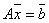 , где А – невырожденная матрица:
, где А – невырожденная матрица:
решение системы имеет вид 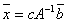 , где с – произвольная постоянная
, где с – произвольная постоянная
имеет единственное решение
система может быть решена методом Крамера
систему нельзя решить методом Крамера
Для системы уравнений 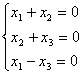 справедливы утверждения:
справедливы утверждения:
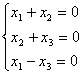 справедливы утверждения:
справедливы утверждения:система имеет множество решений V и dim V = 2
решение системы единственно, 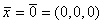
фундаментальная система решений состоит из 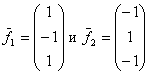
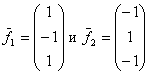
Выражение вида a + bi, где a, b – действительные числа, i2 = -1, называется __________ числом (слово)
Матрица 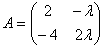 является вырожденной при
является вырожденной при 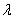 , равном:
, равном:
только при 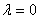
при всех 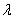
только при 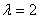
ни при каком значении 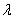
Матрица, определитель которой равен нулю, называется ____________ (вставьте слово)
Дана матрица 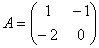 , вектор – столбец
, вектор – столбец 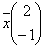 и вектор – строка
и вектор – строка 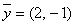 Укажите верные соответствия:
Укажите верные соответствия:
умножение невозможно
(4, - 2)
Ранг вырожденной матрицы четвертого порядка:
равен 4
больше 4
меньше 4
равен 0
Результатом выполнения действий в выражении (3i + i3)2 является число Z
алгебраическая форма которого имеет вид -4
аргумент которого arg Z = 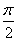
тригонометрическая форма Z имеет вид: 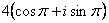
модуль 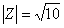
Система линейных уравнений совместима тогда и только тогда, когда ранг матрицы А __________ рангу расширенной матрицы 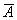 (вставить слово)
(вставить слово)
При транспонировании определитель ________________________ (что делает? Меняет знак или не изменяется Выберите верный ответ)
Если detA 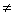 0, тогда:
0, тогда:
система 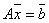 имеет единственное решение
имеет единственное решение
r(A) меньше порядка матрицы
система 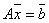 может быть решена методом Крамера
может быть решена методом Крамера
С помощью элементарных преобразований Гаусса произвольную матрицу можно привести к _________ виду (вставить слово)
Система уравнений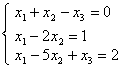 :
:
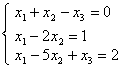 :
:имеет единственное решение
имеет множество решений
решением системы является вектор 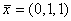
несовместима
Система уравнений 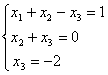 имеет:
имеет:
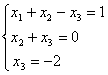 имеет:
имеет:множество решений
единственное решение (–3, 2, –2)
система несовместима
единственное решение (3, 2, –2)
Матрица 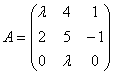 не имеет обратной при
не имеет обратной при 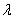 , равном:
, равном:
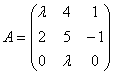 не имеет обратной при
не имеет обратной при только при 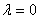
0 и -2
ни при каком 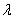
только при 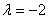
Для системы уравнений 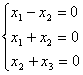 справедливы утверждения:
справедливы утверждения:
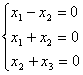 справедливы утверждения:
справедливы утверждения:фундаментальная система решений может состоять из одного вектора 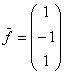
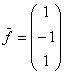
определитель системы det A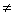 0
0
имеет подпространство решений V и его размерность dim V = 1
система имеет единственное решение 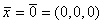
Если ранг системы из m векторов равен m, то эти векторы линейно ___________ (слово)
Результатом выполнения действий в выражении 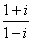 является число Z
является число Z
arg Z = 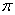
алгебраическая форма которого имеет вид Z = i
тригонометрическая форма Z имеет вид: 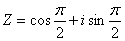
Если квадратные матрицы А и В перестановочны и АВ = ВА = Е, то матрица В является _________ для матрицы А (вставьте слово)
Теорема, определяющая критерий совместности системы линейных уравнений, носит название ________ (вставить название теоремы)
 равен:
равен: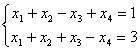 имеет вид:
имеет вид: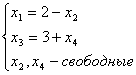
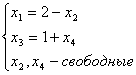
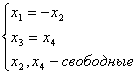
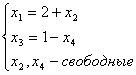
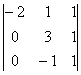 равен:
равен: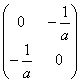
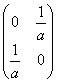
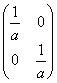
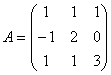 равен:
равен: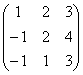 равна:
равна:
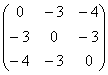
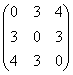
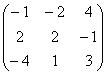 имеет вид:
имеет вид: